SVG-Transformationen – Grundlagen, SVG-Codebeispiele
SVG ermöglicht die Änderung grafischer Elemente durch Übersetzung, Drehung, Skalierung und Neigung. Alle diese SVG-Transformationen beziehen sich auf die geometrische Art. SVG-Objekte können mithilfe der Eigenschaften des transform-Attributs geändert werden: translate, scale, rotate, skewX, skewY und matrix.
Übersetzung – Translation
Die Translation verschiebt alle Objektpunkte im gleichen Abstand entlang paralleler Linien. Dies kann als Verschiebung des Ursprungs des Koordinatensystems des Elements interpretiert werden. Es gibt drei Transformationsfunktionen: translateX (tx), translateY (ty) und translate (tx, ty). Die Funktion translate (tx, ty) verschiebt ein Element um einen tx-Wert entlang der x-Achse und um ty entlang der y-Achse. Wenn einer der Werte nicht angegeben ist, wird er standardmäßig auf Null gesetzt.
Die Aktion des Attributs transform="translate(tx, ty)" bedeutet die Änderung der Objektkoordinaten gemäß der Formel:
x(neu) = x(alt) + tx
y(neu) = y(alt) + ty
Hier ist ein einfaches Beispiel:
1<svg viewBox="0 0 100 100" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation -->
6 <circle cx="15" cy="15" r="10" stroke="black" transform="translate(22)" />
7 <circle cx="15" cy="15" r="10" stroke="red" transform="translate(44)" />
8 <!-- both horizontal and vertical translation -->
9 <circle cx="15" cy="15" r="10" stroke="green" transform="translate(33,13)" />
10 <circle cx="15" cy="15" r="10" stroke="yellow" transform="translate(11,13)" />
11 </g>
12</svg>Im Codebeispiel wird das Element <g> verwendet, um Kreise zu gruppieren. Das fill-Attribut gilt innerhalb von <g> einmal für alle Formen. Hier ist das resultierende Bild (
translation.svg):

Skalierung – Scaling
Skalierung ist eine SVG-Transformation, die ein Objekt mithilfe eines Skalierungsfaktors vergrößert oder verkleinert. Man muss zwischen gleichmäßiger und gerichteter Skalierung unterscheiden.
Die Transformationsfunktion scale (sx [sy]) ermöglicht die Skalierung des Bildes entlang der x- und y-Achse. Diese Funktion akzeptiert einen oder zwei Werte, die die horizontale und vertikale Skalierung angeben: transform="scale(<sx> [<sy>])". Der Skalierungsfaktorwert sy ist optional und wenn er weggelassen wird, wird davon ausgegangen, dass er gleich sx ist.
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale -->
3 <circle cx="0" cy="0" r="10" fill="#B0C4DE" transform="scale(4)" />
4 <circle cx="0" cy="0" r="10" fill="#DDA0DD" transform="scale(3)" />
5 <circle cx="0" cy="0" r="10" fill="#FFB6C1" transform="scale(2)" />
6 <!-- no scale -->
7 <circle cx="0" cy="0" r="10" fill="#5F9EA0" />
8 <g transform="translate(100)">
9 <!-- uniform scale -->
10 <circle cx="0" cy="0" r="10" fill="#B0C4DE" transform="scale(4)" />
11 <!-- vertical scale -->
12 <circle cx="0" cy="0" r="10" fill="#DDA0DD" transform="scale(1,4)" />
13 <!-- horizontal scale -->
14 <circle cx="0" cy="0" r="10" fill="#FFB6C1" transform="scale(4,1)" />
15 <!-- no scale -->
16 <circle cx="0" cy="0" r="10" fill="#5F9EA0" />
17 </g>
18</svg>Hier ist das resultierende Bild ( scaling.svg):
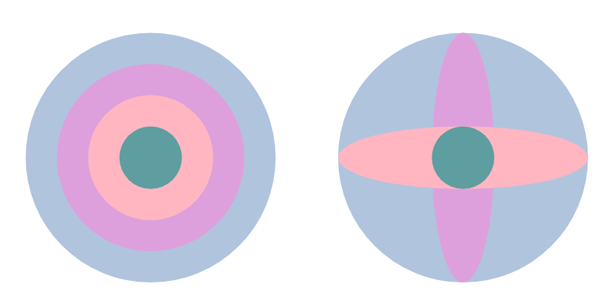
Der obige Code verwendet die Funktionen scale und translate. Die erste Gruppe von Kreisen in der Abbildung zeigt ein Beispiel für eine gleichmäßige Skalierung, und die zweite Gruppe veranschaulicht die Kreisskalierung entlang der y-Achse (Linie 12) und der x-Achse (Linie 14). Ein Skalierungswert von „4“ rendert eine Grafik auf das Vierfache ihrer ursprünglichen Größe, während ein Wert von „4,1“ ihre Quellbreite um das Vierfache vergrößert und ihre Höhe speichert.
Sie können die Größe von SVG in C# mithilfe der Aspose.SVG für .NET-API ändern. Der Artikel
SVG-Skalierung – C#-Beispiele behandelt C#-Beispiele für die SVG-Skalierung. Sie finden Fälle der Verwendung der Funktion scale() im Attribut transform sowie einer Transformationsmatrix – matrix(a,b,c,d,e,f).
SVG-Rotation
Die Funktion rotate(angle, cx, cy) dreht das Element um angle um den Punkt mit den Koordinaten (cx, cy). Wenn keine Koordinaten angegeben sind, erfolgt die Drehung um den Punkt (0, 0) des ursprünglichen Koordinatensystems. Alle Dreh- oder Neigungswinkelwerte sollten in Grad angegeben werden. Sie können die anderen in CSS verfügbaren Einheiten nicht verwenden. Wenn wir einen positiven Winkelwert verwenden, erfolgt die Drehung im Uhrzeigersinn, und umgekehrt gibt uns ein negativer Winkelwert eine Drehung gegen den Uhrzeigersinn.
Hinweis: Wenn Sie nur den angle und den Parameter cx angeben, wird der Wert ungültig und es wird keine SVG-Rotation angewendet.
Wie bei der translation verzerrt auch die SVG-Rotation das Element nicht und spart Parallelität, Winkel und Abstände.
1<svg width="450" height="450" xmlns="http://www.w3.org/2000/svg">
2 <rect x="100" y="250" width="200" height="30" fill="CadetBlue" />
3 <rect x="100" y="250" width="200" height="30" fill="#DDA0DD" transform ="rotate(-45 200 265)" />
4 <rect x="100" y="250" width="200" height="30" fill="Pink" transform ="rotate(-90 200 265)" />
5 <rect x="100" y="250" width="200" height="30" fill="#B0C4DE" transform ="rotate(45 200 265)" />
6 <rect x="100" y="250" width="200" height="30" fill="CadetBlue" transform ="rotate(-35)" />
7</svg>Die in Zeile 4 verwendete Funktion transform="rotate(-90 200 265)" bedeutet, dass das rosa Rechteck um 90 Grad gegen den Uhrzeigersinn gedreht werden soll, wobei der Drehpunkt bei (200,265) liegt. Für das Rechteck in Zeile 6 werden die Koordinaten (cx, cy) nicht angegeben und die Drehung um -35 Grad erfolgt um den Punkt (0, 0) des ursprünglichen Koordinatensystems. Das Ergebnis der SVG-Rotation ist in der Abbildung zu sehen:
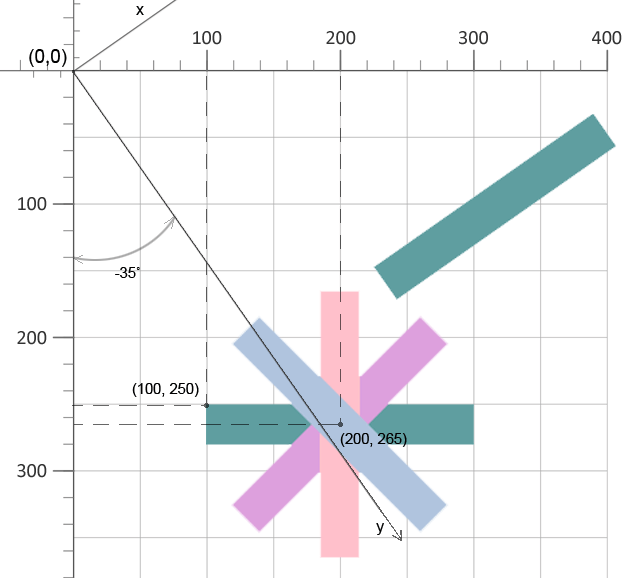
Sie können die Datei, die die SVG-Rotation veranschaulicht, anzeigen und anschließend speichern, indem Sie auf den Link rotation.svg klicken.
Sie können SVG in C# mithilfe der Aspose.SVG für die .NET-API drehen. Der Artikel
SVG drehen – C#-Beispiele behandelt C#-Beispiele für die SVG-Rotation. Es werden Fälle der Verwendung der Funktion rotate() im Attribut transform und der Transformationsmatrix matrix(a,b,c,d,e,f) betrachtet.
Schrägstellung – Skewing
Schrägstellung ist eine Transformation, die eine der Achsen des Koordinatensystems des Elements um einen bestimmten Winkel im oder gegen den Uhrzeigersinn dreht. SVG-Elemente können mithilfe der Funktionen skewX(angle) und skewY(angle) verzerrt werden. Der in diesen Funktionen enthaltene angle-Wert stellt eine schräge SVG-Transformation in Grad entlang der entsprechenden Achse dar. Bei Verwendung von skewX(angle) ändert sich nur die x-Koordinate der Punkte der Form, die y-Koordinate bleibt jedoch unverändert. Die Funktion skewX(angle) lässt die vertikalen Linien so aussehen, als wären sie um einen bestimmten Winkel gedreht worden. Die x-Koordinate jedes Punkts ändert sich auf einen Wert, der proportional zum angegebenen Winkel und Abstand zum Ursprung ist.
Hier wird ein Beispiel des Kreises mit dem skewX(55)-Wert ( sqew-x.svg) gezeigt:
1<svg viewBox="0 0 100 100" xmlns="http://www.w3.org/2000/svg">
2 <circle cx="20" cy="20" r="15" stroke="blue" fill="none" />
3 <circle cx="20" cy="20" r="15" stroke="grey" stroke-opacity="0.7" fill="none" transform="skewX(55)" />
4</svg>Ein einfaches Beispiel für das durch die Funktion skewY(35) verzerrte Rechteck ( sqew-y.svg):
1<svg width="800" height="800" viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <rect x="20" y="20" width="30" height="30" stroke="blue" stroke-opacity="1" fill="none" />
3 <rect x="20" y="20" width="30" height="30" stroke="grey" stroke-opacity="0.5" fill="none" transform="skewY(35)" />
4 </svg>Die gerenderten Beispiele sehen so aus:
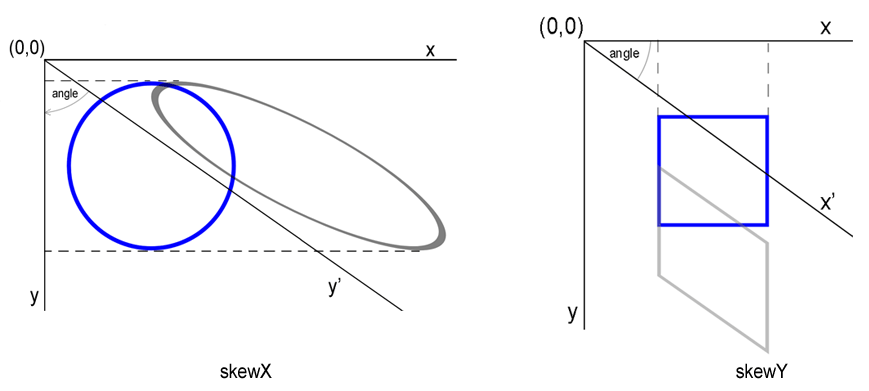
Um zu erfahren, wie Sie eine Transformationsmatrix zum Drehen, Skalieren, Übersetzen und Verzerren von SVG-Grafiken verwenden und SVG-Codebeispiele betrachten, lesen Sie bitte den Artikel
Transformationsmatrix.
Lesen Sie den Artikel
SVG-Transformationen – C#-Beispiele, um C#-Codebeispiele zum Drehen, Skalieren, Verschieben und Neigen von SVG-Grafiken mithilfe der Aspose.SVG für .NET-Bibliothek zu erhalten.
Aspose.SVG bietet SVG-kostenlose Webanwendungen zum Konvertieren von SVG- oder Bilddateien, Zusammenführen von SVG-Dateien, Bildvektorisierung, SVG-Sprite-Generierung, SVG-zu-Base64-Datenkodierung und Textvektorisierung. Diese Online-Apps funktionieren auf jedem Betriebssystem mit einem Webbrowser und erfordern keine zusätzliche Softwareinstallation. Es ist eine schnelle und einfache Möglichkeit, Ihre SVG-bezogenen Aufgaben effizient und effektiv zu lösen!