Analyzing your prompt, please hold on...
An error occurred while retrieving the results. Please refresh the page and try again.
Scalable Vector Graphics (SVG) ist eine XML-Sprache zum Erstellen zweidimensionaler Vektor- und gemischter Vektor-/Rastergrafiken. Und eine Transformationsmatrix ist eine Matrix, die im Prozess der Matrixmultiplikation einen Vektor in einen anderen Vektor transformiert. Es ist also ein praktisches Werkzeug zum Anwenden von SVG-Transformationen wie Translation, Rotation, Skalierung und Skewing. Transformationsmatrizen basieren auf der linearen Algebra, die eine mathematisch elegante Möglichkeit bietet, komplexe Transformationen auszudrücken. Diese mathematische Grundlage erleichtert Entwicklern und Designern mit mathematischem Hintergrund die Arbeit mit SVG-Transformationen.
Schauen wir uns genauer an, wie es funktioniert!
Die Transformationsmatrix ist 3x3 und kombiniert Translations-, Skalierungs-, Rotations- und Schrägtransformationen. Hier ist, was jedes Element darstellt:
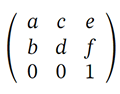
a – es kann sich um einen Skalierungsfaktor in x-Richtung handeln, der normalerweise als sx oder als Kosinuswert cos(α) des zu drehenden Winkels bezeichnet wird
b – es kann sich um den Neigungsfaktor tan(α) in der y-Richtung oder um den Sinuswert sin(α) des zu drehenden Winkels handeln
c – es kann sich um den Versatzfaktor tan(α) in der x-Richtung oder um den Sinuswert -sin(α) des zu drehenden Winkels handeln
d – es kann sich um einen Skalierungsfaktor in y-Richtung handeln, der normalerweise als sy oder als Kosinuswert cos(α) des zu drehenden Winkels bezeichnet wird
e – Translation entlang der x-Richtung wird normalerweise als tx bezeichnet
f – die Verschiebung entlang der y-Richtung wird normalerweise als ty bezeichnet
Mit der Transformationsmatrix können Sie während der Transformation neue Koordinaten der Punkte des Objekts (x new, y new) erhalten, indem Sie diese mit den Werten der vorherigen Koordinaten (x prev, y prev) multiplizieren:
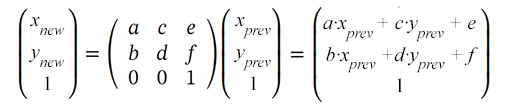
SVG-Objekte können mithilfe der Matrixeigenschaft des Transformationsattributs geändert werden: transform=“matrix(a,b,c,d,e,f)”. Es können nur die ersten 6 Werte angegeben werden. Sie stellen der Matrixtransformationsfunktion also sechs Werte zur Verfügung, um die Verschiebung, Skalierung, Drehung und Neigung festzulegen.
Die translation ist eine Transformation in SVG, die alle Punkte eines Objekts im gleichen Abstand entlang paralleler Linien verschiebt. Diese Transformation verschiebt den Ursprung des Koordinatensystems des Elements. Die Übersetzungsmatrix sieht folgendermaßen aus:
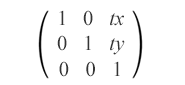
matrix(1,0,0,1,tx,ty)
Die Übersetzungsmatrix kombiniert die Werte tx und ty, um ein Element horizontal und vertikal zu verschieben. Es verschiebt das Objekt um tx entlang der x-Achse und um ty entlang der y-Achse.
Schauen Sie sich das Beispiel mit dem ursprünglichen blauen Rechteck an, das sich entlang der x-Achse (rot), der y-Achse (orange) und beiden (grün) verschiebt:
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation by tx=30 -->
6 <circle cx="15" cy="15" r="10" stroke="red" transform="matrix(1 0 0 1 30 0)" />
7 <!-- vertical translation by by ty=25 -->
8 <circle cx="15" cy="15" r="10" stroke="orange" transform="matrix(1 0 0 1 0 25)" />
9 <!-- both horizontal and vertical translation by tx=30 and by ty=25 -->
10 <circle cx="15" cy="15" r="10" stroke="green" transform="matrix(1 0 0 1 30 25)" />
11 </g>
12</svg>Die Aktion des Attributs transform=“matrix(1,0,0,1,tx,ty)” bedeutet die Änderung der Objektkoordinaten gemäß der Formel:
x(new) = a·x(prev) + b·y(prev) +e = x(prev) + tx
y(new) = b·x(prev) + d·y(prev) +f = y(prev) + ty
Im Codebeispiel wird das Element <g> verwendet, um Kreise zu gruppieren. Das fill-Attribut gilt innerhalb von <g> einmal für alle Formen. Hier ist das resultierende Bild:

Skalierung ist eine SVG-Transformation, die ein Objekt mithilfe eines Skalierungsfaktors vergrößert oder verkleinert. Eine Skalierungsmatrix wird verwendet, um Objekte gleichmäßig oder ungleichmäßig entlang der Koordinatenachsen zu skalieren. sx und sy sind die Skalierungsfaktoren für die x- und y-Achsen. Wenn sx und sy größer als 1 sind, wird das Objekt vergrößert; liegen sie zwischen 0 und 1, wird das Objekt verkleinert. Wenn die Skalierungsfaktoren auf unterschiedliche Werte eingestellt sind, ist die Skalierung des Objekts ungleichmäßig, was zu einem Streckungs- oder Schrumpfungseffekt führt.
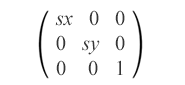
matrix(sx,0,0,sy,0,0)
Schauen Sie sich das Beispiel mit dem ursprünglichen blauen Rechteck an, das relativ zum Ursprung (0, 0) gleichmäßig und ungleichmäßig skaliert – Bilder a und b – und relativ zum Punkt (10, 10) gleichmäßig skaliert – Bild c:
1<svg viewBox="0 0 400 300" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale is shown in fig.a -->
3 <g fill="none">
4 <rect x="10" y="10" width="20" height="20" stroke="blue" />
5 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, 0, 0)" />
6 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, 0, 0)" />
7 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 0, 0)" />
8 </g>
9 <!-- non-uniform scale is shown in fig.b -->
10 <g transform="translate(70)">
11 <rect x="10" y="10" width="20" height="20" fill="blue" />
12 <rect x="10" y="10" width="20" height="20" fill="red" transform="matrix(1.5, 0, 0, 2, 0, 0)" />
13 <rect x="10" y="10" width="20" height="20" fill="orange" transform="matrix(3, 0, 0, 2.5, 0, 0)" />
14 <rect x="10" y="10" width="20" height="20" fill="green" transform="matrix(0.7, 0, 0, 0.5, 0, 0)" />
15 </g>
16 <!-- uniform scale relative to point (10, 10) is shown in fig.c -->
17 <g fill="none" transform="translate(170)">
18 <rect x="10" y="10" width="20" height="20" stroke="blue" />
19 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, -5, -5)" />
20 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, -10, -10)" />
21 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 3, 3)" />
22 </g>
23</svg>Hier ist das resultierende Bild:
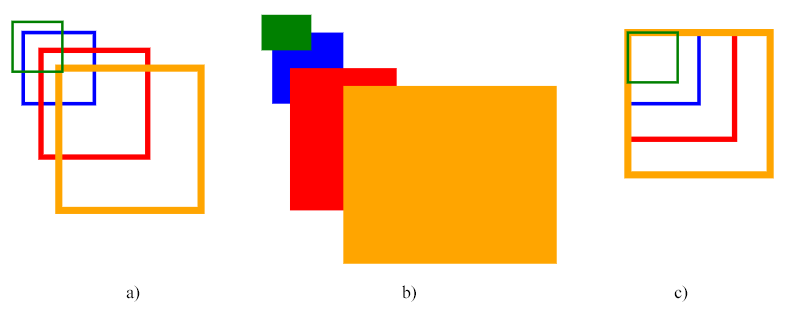
Der obige Code verwendet die Skalenmatrix. Die erste Gruppe von Rechtecken in der Abbildung zeigt ein Beispiel für eine gleichmäßige Skalierung (Abb. a), die zweite Gruppe zeigt die ungleichmäßige Skalierung (Abb. b) und die dritte Gruppe von Rechtecken zeigt die gleichmäßige Skalierung relativ zum Punkt (10, 10) – die obere linke Ecke für das blaue (Quellen-)Rechteck.
Hinweis: Die Skalierung erfolgt relativ zum Ursprung (0, 0) des Koordinatensystems. Wenn der Punkt (cx, cy) des SVG-Objekts (zu dem es relativ gezeichnet wird) nicht am Ursprung liegt, verschiebt die Anwendung einer Skalierungstransformation die Position des Objekts, was den Eindruck einer Übersetzung erwecken kann. Wir sehen den Effekt der Verschiebung der Rechtecke in den Abbildungen a und b.
Um um einen bestimmten Drehpunkt (сx, сy) herum zu skalieren, müssen Sie eine zusätzliche Bewegung auf die skalierte Form anwenden, um sie zum Drehpunkt zu verschieben (Abb. c). Vollständige Transformationsmatrix, die Übersetzung und Skalierung kombiniert:
matrix(sx,0,0,sy,cx·(1-sx),cy·(1-sy))
Diese Matrix skaliert das Objekt korrekt um den Drehpunkt (cx, cy) ohne jegliche Verschiebung. Die Koeffizienten cx·(1-sx) und cy·(1-sy) übernehmen die notwendige Übersetzung, um sicherzustellen, dass das Objekt nach der Skalierung an seiner ursprünglichen Position bleibt. Berechnen wir diese Werte für das rote Rechteck (Abb. c). Der Drehpunkt (cx, cy) in diesem Beispiel ist (10, 10) – die obere linke Ecke des blauen (anfänglichen) Rechtecks:
cx·(1-sx)=10·(1-1,5)=10·(-0,5)=-5
cy·(1-sy)=10·(1-1,5)=10·(-0,5)=-5
Sie können die Größe von SVG in C# mithilfe der Aspose.SVG for .NET-API ändern. Der Artikel
SVG-Skalierung – C#-Beispiele behandelt C#-Beispiele für die SVG-Skalierung. Sie finden Fälle der Verwendung der Funktion scale() im Attribut transform sowie einer Transformationsmatrix – matrix(a,b,c,d,e,f).
Wenn Sie die Berechnung von Sinus und Cosinus üben möchten, sind Sie hier genau richtig! Die Rotationsmatrix sieht so aus:
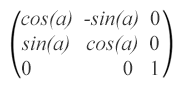
matrix(cos(α),sin(α),-sin(α),cos(α),0,0), wobei α der Winkel um den Punkt mit Koordinaten ist (0, 0) des anfänglichen Koordinatensystems.
Schauen Sie sich das Beispiel mit dem anfänglichen blauen Rechteck an, das um 90° (grün), 180° (grau), 270° (blaugrün), -45° (rot) und 135° (orange) gedreht ist:
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- rotation around point with coordinates (0, 0) is shown in fig.a -->
3 <g>
4 <rect x="0" y="0" width="20" height="20" fill="blue" />
5 <rect x="0" y="0" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
6 <rect x="0" y="0" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
7 <rect x="0" y="0" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
8 <rect x="0" y="0" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
9 <rect x="0" y="0" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
10 <!-- rotation around point with coordinates (0, 0) is shown in fig.b -->
11 </g>
12 <g transform="translate(70)">
13 <rect x="5" y="5" width="20" height="20" fill="blue" />
14 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
15 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
16 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
17 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
18 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
19 </g>
20 <!-- rotation around point with coordinates (5, 5) is shown in fig.c -->
21 <g transform="translate(140)">
22 <rect x="5" y="5" width="20" height="20" fill="blue" />
23 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 10, 0)" />
24 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 10, 10)" />
25 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 10)" />
26 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, -2, 5)" />
27 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 12, 5)" />
28 </g>
29</svg>Hinweis: Wenn wir einen positiven Winkelwert verwenden, erfolgt die Drehung im Uhrzeigersinn, und umgekehrt gibt uns ein negativer Winkelwert eine Drehung gegen den Uhrzeigersinn.
Das Ergebnis der SVG-Rotation ist in der Abbildung zu sehen:
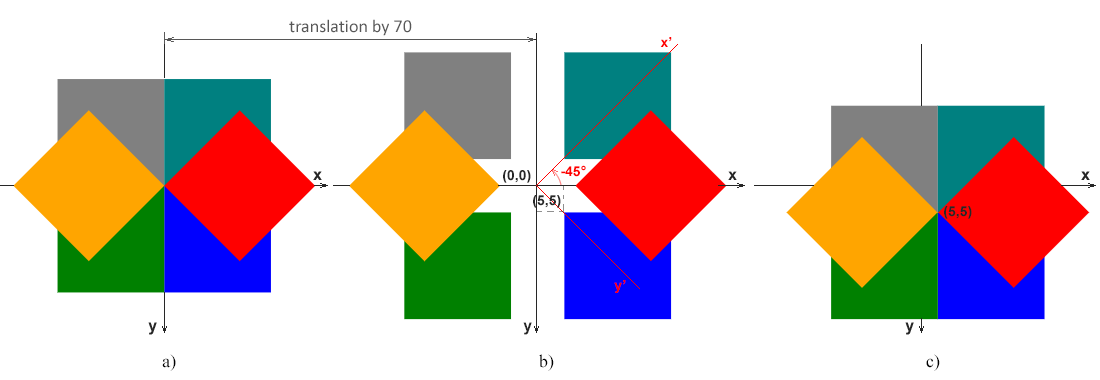
Auf Abb. a zeigt den Fall, wenn die obere linke Ecke des blauen (anfänglichen) Rechtecks (0, 0) mit dem Ursprungspunkt des Koordinatensystems (0, 0) übereinstimmt.
Auf Abb. b veranschaulicht den Fall, dass die obere linke Ecke des blauen (anfänglichen) Rechtecks (5, 5) nicht mit dem Ursprungspunkt (0, 0) übereinstimmt. Diese Abbildung zeigt die x-y-Achsen des ursprünglichen Koordinatensystems, die für alle a-, b- und c-Figuren gelten. Darüber hinaus werden die x’-y’-Achsen des Koordinatensystems für das rote Rechteck, das um 45 Grad gegen den Uhrzeigersinn (α=-45°) gedreht ist, rot angezeigt. Dies zeigt deutlich, dass die Drehung des Rechtecks auf die Drehung des Koordinatensystems reduziert wird.
Auf Abb. c zeigt den Fall, wenn die obere linke Ecke des blauen (anfänglichen) Rechtecks (5, 5) nicht mit dem Anfangspunkt des Koordinatensystems (0, 0) übereinstimmt, die Drehung jedoch um den Punkt (5, 5) erfolgt.
Hinweis: Die folgende Matrix dreht das Objekt um den Drehpunkt (cx, cy):
matrix(cos(α), sin(α), -sin(α), cos(α), cx·(1-cos(α))+cy·sin(α), cy·(1-cos (α))-cx·sin(α))
Die Koeffizienten cx·(1-cos(α))+cy·sin(α) und cy·(1-cos(α))-cx·sin(α) behandeln die notwendige Verschiebung, um sicherzustellen, dass das Objekt nach der Drehung an seiner ursprünglichen Position bleibt. Berechnen wir diese Werte für das rote Rechteck (Abb. c). Der Drehpunkt (cx, cy) in diesem Beispiel ist (5, 5) – die obere linke Ecke des blauen (anfänglichen) Rechtecks, und der Winkel für rotes Rechteck beträgt -45°:
cos(-45°)=0,7071, sin(-45°)=-0,7071
cx·(1-cos(α))+cy·sin(α)=5·(1-0,7071)+5·(-0,7071)=-2
cy·(1-cos(α))-cx·sin(α)=5·(1-0,7071)-5·(-0,7071)=5
Sie können SVG in C# mithilfe der Aspose.SVG für die .NET-API drehen. Der Artikel
SVG drehen – C#-Beispiele behandelt C#-Beispiele für die SVG-Rotation. Es werden Fälle der Verwendung der Funktion rotate() im Attribut transform und der Transformationsmatrix matrix(a,b,c,d,e,f) betrachtet.
Schrägstellung ist eine Transformation, die eine der Achsen des Koordinatensystems des Elements um einen bestimmten Winkel α im oder gegen den Uhrzeigersinn dreht. SVG-Elemente können mithilfe der Verzerrungsmatrix, die wie folgt aussieht, verzerrt werden:
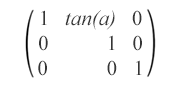
matrix(1,0,tan(α),1,0,0) – Diese Skew-Matrix gibt eine Skew-Transformation entlang der x-Achse um α Grad an.
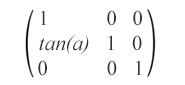
matrix(1,tan(α),0,1,0,0) – Diese Skew-Matrix gibt eine Skew-Transformation entlang der y-Achse um α Grad an.
Hier ist ein Beispiel für den Kreis mit Schrägtransformationen dargestellt:
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <circle cx="20" cy="20" r="10" stroke="blue" />
4 <!-- skew transformation along the x-axis by α=45° -->
5 <circle cx="20" cy="20" r="10" stroke="red" transform="matrix(1,0,1,1,0,0)" />
6 </g>
7 <g fill="none" transform="translate(70)">
8 <circle cx="20" cy="20" r="10" stroke="blue" />
9 <!-- skew transformation along the y-axis by α=45° -->
10 <circle cx="20" cy="20" r="10" stroke="orange" transform="matrix(1,1,0,1,0,0)" />
11 </g>
12</svg>Das gerenderte Beispiel sieht so aus:
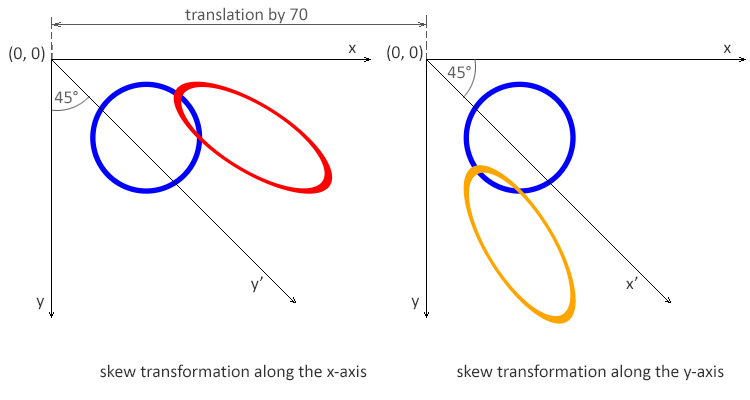
Hinweis: Der Winkelwert α stellt eine schräge SVG-Transformation in Grad entlang der entsprechenden Achse dar. Bei der Schrägtransformation entlang der x-Achse ändert sich nur die x-Koordinate der Punkte der Form, die y-Koordinate bleibt jedoch unverändert. Durch die Schrägtransformation entlang der x-Achse sehen die vertikalen Linien so aus, als wären sie um einen bestimmten Winkel gedreht worden. Die x-Koordinate jedes Punkts ändert sich auf einen Wert, der proportional zum angegebenen Winkel und Abstand zum Ursprung ist.
Die SVG-Transformationsmatrix ist ein leistungsstarkes Werkzeug zum Bearbeiten und Animieren von Objekten in SVG. Es bietet eine vielseitige Möglichkeit, Formen und Elemente zu verschieben, zu drehen, zu skalieren und zu neigen, sodass Sie visuell dynamische und interaktive Grafiken erstellen können. Die Matrix ermöglicht sowohl individuelle als auch kombinierte Transformationen und bietet die Flexibilität, komplexe und komplexe visuelle Effekte zu erzielen. Wir haben in diesem Artikel nur einzelne Transformationen behandelt, aber wir werden versuchen, unseren SVG-Zeichnungsleitfaden bald um neue Artikel mit komplexeren Beispielen zu erweitern.
Um mehr zu erfahren und SVG-Codebeispiele zum Drehen, Skalieren, Verschieben und Neigen von SVG-Grafiken mithilfe des SVG-Transformationsattributs zu erhalten, lesen Sie bitte den Artikel
SVG-Transformation.
Lesen Sie den Artikel
SVG-Transformationen – C#-Beispiele, um C#-Codebeispiele zum Drehen, Skalieren, Übersetzen und Verzerren von SVG-Grafiken mithilfe der Aspose.SVG for .NET-Bibliothek zu erhalten.
Aspose.SVG bietet SVG-kostenlose Webanwendungen zum Konvertieren von SVG- oder Bilddateien, Zusammenführen von SVG-Dateien, Bildvektorisierung, SVG-Sprite-Generierung, SVG-zu-Base64-Datenkodierung und mehr. Diese Online-Anwendungen funktionieren auf jedem Betriebssystem mit einem Webbrowser und erfordern keine zusätzliche Softwareinstallation. Es ist eine schnelle und einfache Möglichkeit, Ihre SVG-bezogenen Aufgaben effizient und effektiv zu lösen!
Analyzing your prompt, please hold on...
An error occurred while retrieving the results. Please refresh the page and try again.