Transformation Matrix – SVG Code Examples
Scalable Vector Graphics (SVG) is an XML language for creating two-dimensional vector and mixed vector/raster graphics. And a transformation matrix is a matrix that transforms one vector into another vector in the process of matrix multiplication. So, it is a convenient tool for applying SVG transformations like translation, rotation, scaling, and skewing. Transformation matrices are based on linear algebra, which offers a mathematically elegant way to express complex transformations. This math foundation makes it easier for developers and designers with math backgrounds to work with SVG transformations.
Let’s take a closer look at how it works!
Transformation Matrix
The transformation matrix is 3x3, combining translation, scale, rotation, and skew transformations. Here’s what each element represents:
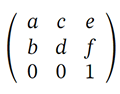
a – it can be a scaling factor in the x-direction, usually denoted as sx or the cosine value cos(α) of the angle to rotate
b – it can be tan(α) skewing factor in the y-direction or the sinus value sin(α) of the angle to rotate
c – it can be tan(α) skewing factor in the x-direction or the sinus value -sin(α) of the angle to rotate
d – it can be scaling factor in the y-direction is usually denoted as sy or the cosine value cos(α) of the angle to rotate
e – translation along the x-direction is usually denoted as tx
f – translation along the y-direction is usually denoted as ty
The transformation matrix allows you to get new coordinates of the object’s points (x new, y new) during the transformation by multiplying it by the values of the previous coordinates (x prev, y prev):
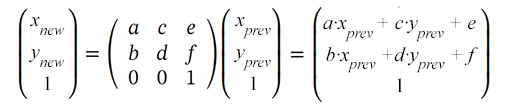
SVG objects can be altered using the matrix property of the transform attribute: transform=“matrix(a,b,c,d,e,f)”. Only the first 6 values can be specified. So you provide 6 values to the matrix transformation function to set translation, scaling, rotation, and skewing.
Translation Matrix
The translation is a transformation in SVG that moves all the points of an object at the same distance along parallel lines. This transformation shifts the origin of the element’s coordinate system. The translation matrix looks like this:
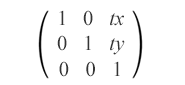
matrix(1,0,0,1,tx,ty)
The translate matrix combines both tx and ty values to move an element horizontally and vertically. It shifts the object by tx along the x-axis and by ty along the y-axis.
Look at the example with the original blue rectangle that translates along the x-axis (red), y-axis (orange), and both (green):
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation by tx=30 -->
6 <circle cx="15" cy="15" r="10" stroke="red" transform="matrix(1 0 0 1 30 0)" />
7 <!-- vertical translation by by ty=25 -->
8 <circle cx="15" cy="15" r="10" stroke="orange" transform="matrix(1 0 0 1 0 25)" />
9 <!-- both horizontal and vertical translation by tx=30 and by ty=25 -->
10 <circle cx="15" cy="15" r="10" stroke="green" transform="matrix(1 0 0 1 30 25)" />
11 </g>
12</svg>The action of attribute transform=“matrix(1,0,0,1,tx,ty)” means the changing of object coordinates according to the formula:
x(new) = a·x(prev) + b·y(prev) +e = x(prev) + tx
y(new) = b·x(prev) + d·y(prev) +f = y(prev) + ty
In the code example, <g> element is used to group circles together. The fill attribute applies inside <g> to all shapes once. Here is the resulting image:

Scaling Matrix
Scaling is an SVG transformation that enlarges or reduces an object using a scaling factor. A scaling matrix is used to scale objects uniformly or non-uniformly along the coordinate axes. sx and sy are the scaling factors for the x and y axes. If sx and sy are greater than 1, the object will be scaled up; if they are between 0 and 1, the object will be scaled down. If the scale factors are set to different values, the scale of the object will be uneven, resulting in a stretching or shrinking effect. The scaling matrix looks like this:
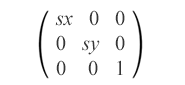
matrix(sx,0,0,sy,0,0)
Look at the example with the original blue rectangle that scales uniformly and non-uniformly, relative to the origin (0, 0) – pictures a and b, and scales uniformly relative to the point (10, 10) – picture c:
1<svg viewBox="0 0 400 300" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale is shown in fig.a -->
3 <g fill="none">
4 <rect x="10" y="10" width="20" height="20" stroke="blue" />
5 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, 0, 0)" />
6 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, 0, 0)" />
7 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 0, 0)" />
8 </g>
9 <!-- non-uniform scale is shown in fig.b -->
10 <g transform="translate(70)">
11 <rect x="10" y="10" width="20" height="20" fill="blue" />
12 <rect x="10" y="10" width="20" height="20" fill="red" transform="matrix(1.5, 0, 0, 2, 0, 0)" />
13 <rect x="10" y="10" width="20" height="20" fill="orange" transform="matrix(3, 0, 0, 2.5, 0, 0)" />
14 <rect x="10" y="10" width="20" height="20" fill="green" transform="matrix(0.7, 0, 0, 0.5, 0, 0)" />
15 </g>
16 <!-- uniform scale relative to point (10, 10) is shown in fig.c -->
17 <g fill="none" transform="translate(170)">
18 <rect x="10" y="10" width="20" height="20" stroke="blue" />
19 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, -5, -5)" />
20 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, -10, -10)" />
21 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 3, 3)" />
22 </g>
23</svg>Here is the resulting image:
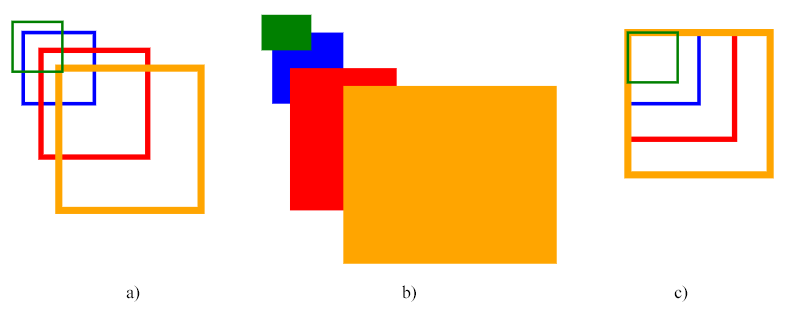
The code above uses the scale matrix. The first group of rectangles on the figure displays an example of uniform scaling (fig. a), the second group illustrates the non-uniform scaling (fig. b), and the third group of rectangles shows the uniform scaling relative to point (10, 10) – the top-left corner for the blue (source) rectangle.
Note: The scaling is performed relative to the origin (0, 0) of the coordinate system. If the point (cx, cy) of the SVG object( it is drawn relative to) is not at the origin, applying a scaling transform will shift the position of the object, which can give the impression of translation. We see the effect of the rectangles’ translation in figures a and b.
In order to scale around a specific pivot point (сx, сy), you need to apply an additional move to the scaled shape to move it to the pivot point (fig. c). Full transformation matrix combining translation and scaling:
matrix(sx,0,0,sy,cx·(1-sx),cy·(1-sy))
This matrix will correctly scale the object around the pivot point (cx, cy) without any translation. The cx·(1-sx) and cy·(1-sy) coefficients handle the necessary translation to ensure the object remains at its original position after scaling. Let’s calculate these values for the red rectangle (fig. c). The pivot point (cx, cy) in this example is (10, 10) – the top-left corner of the blue (initial) rectangle:
cx·(1-sx)=10·(1-1.5)=10·(-0.5)=-5
cy·(1-sy)=10·(1-1.5)=10·(-0.5)=-5
You can resize SVG in C# using Aspose.SVG for .NET API. The
SVG Scaling – C# Examples article covers C# examples for SVG scaling. You will find cases of using the scale() function in the transform attribute as well as a transformation matrix – matrix(a,b,c,d,e,f).
Rotation Matrix
If you like to practice calculating sines and cosines, you are here! The rotation matrix looks like this:
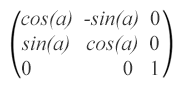
matrix(cos(α),sin(α),-sin(α),cos(α),0,0), where α is the angle around the point with coordinates (0, 0) of the initial coordinate system.
Look at the example with initial blue rectangle, wich is rotated on 90° (green), 180° (grey), 270° (teal), -45° (red), and 135° (orange):
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- rotation around point with coordinates (0, 0) is shown in fig.a -->
3 <g>
4 <rect x="0" y="0" width="20" height="20" fill="blue" />
5 <rect x="0" y="0" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
6 <rect x="0" y="0" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
7 <rect x="0" y="0" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
8 <rect x="0" y="0" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
9 <rect x="0" y="0" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
10 <!-- rotation around point with coordinates (0, 0) is shown in fig.b -->
11 </g>
12 <g transform="translate(70)">
13 <rect x="5" y="5" width="20" height="20" fill="blue" />
14 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
15 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
16 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
17 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
18 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
19 </g>
20 <!-- rotation around point with coordinates (5, 5) is shown in fig.c -->
21 <g transform="translate(140)">
22 <rect x="5" y="5" width="20" height="20" fill="blue" />
23 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 10, 0)" />
24 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 10, 10)" />
25 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 10)" />
26 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, -2, 5)" />
27 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 12, 5)" />
28 </g>
29</svg>Note: If we use a positive angle value, then the rotation will be clockwise, and conversely, a negative angle value gives us counterclockwise spin.
The result of SVG rotation can be seen on the figure:
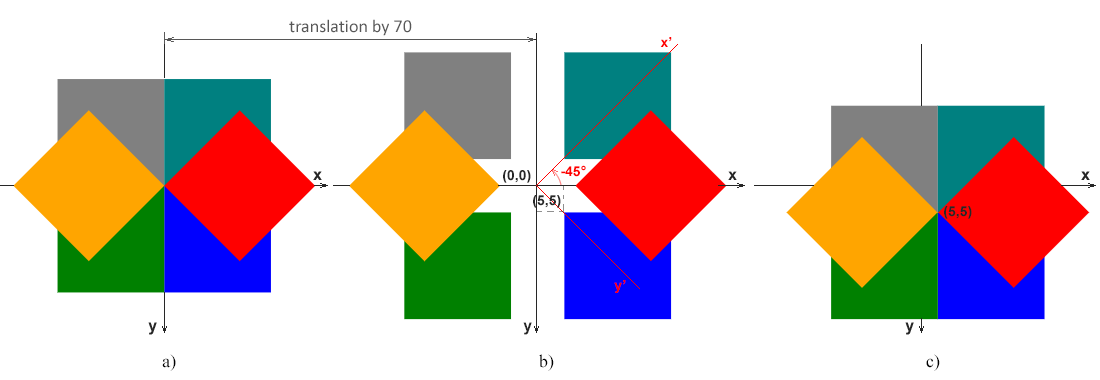
On fig. a shows the case when the top-left corner of the blue (initial) rectangle (0, 0) matches the origin point of the coordinate system (0, 0).
On fig. b illustrates the case when the top-left corner of the blue (initial) rectangle (5, 5) does not match with the point of origin (0, 0). This figure shows the x-y axes of the original coordinate system, which are valid for all a, b, and c figures. In addition, the x’-y’ axes of the coordinate system for the red rectangle, which is rotated 45 degrees counterclockwise α=-45°, are shown in red. This clearly displays that the rotation of the rectangle is reduced to the rotation of the coordinate system.
On fig. c shows the case when the top-left corner of the blue (initial) rectangle (5, 5) does not match the initial point of the coordinate system (0, 0), but the rotation occurs around the point (5, 5).
Note: The following matrix will rotate the object around the pivot point (cx, cy):
matrix(cos(α), sin(α), -sin(α), cos(α), cx·(1-cos(α))+cy·sin(α), cy·(1-cos(α))-cx·sin(α))
The cx·(1-cos(α))+cy·sin(α) and cy·(1-cos(α))-cx·sin(α) coefficients handle the necessary translation to ensure the object remains at its original position after rotation. Let’s calculate these values for the red rectangle (fig. c). The pivot point (cx, cy) in this example is (5, 5) – the top-left corner of the blue (initial) rectangle, and the angle for red rectangle is -45°:
cos(-45°)=0.7071, sin(-45°)=-0.7071
cx·(1-cos(α))+cy·sin(α)=5·(1-0.7071)+5·(-0.7071)=-2
cy·(1-cos(α))-cx·sin(α)=5·(1-0.7071)-5·(-0.7071)=5
You can rotate SVG in C# using Aspose.SVG for .NET API. The
Rotate SVG – C# Examples article covers C# examples for SVG rotation. It considers cases of using the rotate() function in the transform attribute and the transformation matrix – matrix(a,b,c,d,e,f).
Skewing Matrix
Skewing is a transformation that rotates one of the axes of the element’s coordinate system by a certain angle α clockwise or counterclockwise. SVG elements can be skewed through the use of the skewing matrix that looks like this:
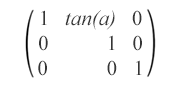
matrix(1,0,tan(α),1,0,0) – This skew matrix specifies a skew transformation along the x-axis by α degrees.
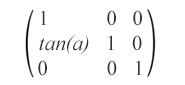
matrix(1,tan(α),0,1,0,0) – This skew matrix specifies a skew transformation along the y-axis by α degrees.
Here is shown an example of the circle with skew transformations:
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <circle cx="20" cy="20" r="10" stroke="blue" />
4 <!-- skew transformation along the x-axis by α=45° -->
5 <circle cx="20" cy="20" r="10" stroke="red" transform="matrix(1,0,1,1,0,0)" />
6 </g>
7 <g fill="none" transform="translate(70)">
8 <circle cx="20" cy="20" r="10" stroke="blue" />
9 <!-- skew transformation along the y-axis by α=45° -->
10 <circle cx="20" cy="20" r="10" stroke="orange" transform="matrix(1,1,0,1,0,0)" />
11 </g>
12</svg>The rendered example look like:
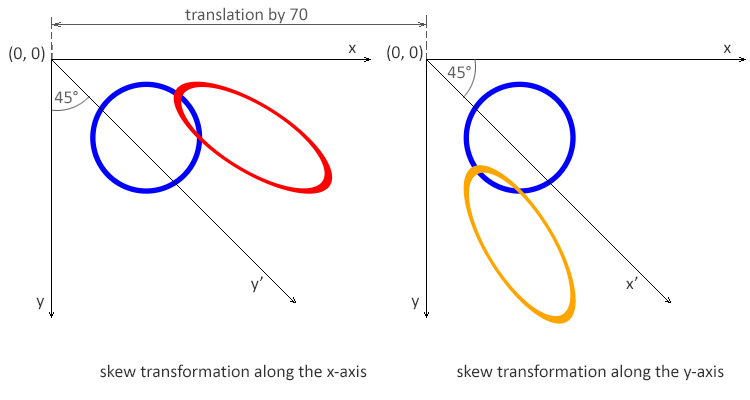
Note: The angle value α represents a skew SVG transformation in degrees along the appropriate axis. The using skew transformation along the x-axis, only the x coordinate of the points of the shape changes, but the y coordinate remains unchanged. The skew transformation along the x-axis makes the vertical lines look like they have been rotated by a given angle. The x coordinate of each point changes on a value proportional to the specified angle and distance to the origin.
Conclusion
The SVG transformation matrix is a powerful tool for manipulating and animating objects in SVG. It provides a versatile way to apply translation, rotation, scaling, and skew to shapes and elements, allowing you to create visually dynamic and interactive graphics. The matrix allows for both individual and combined transformations, offering the flexibility to achieve complex and intricate visual effects. We’ve only covered individual transformations in this article, but we’ll try to expand our SVG Drawing guide soon with new articles with more complex examples.
To learn more and get SVG code examples for rotating, scaling, moving, and skewing SVG graphics using the SVG transform attribute, please go to the SVG Transformation article.
Read the SVG Transformations – C# Examples article to get C# code examples for rotating, scaling, translating, and skewing SVG graphics using Aspose.SVG for .NET library.
Aspose.SVG offers SVG Free Web Applications for converting SVG or image files, merging SVG files, image vectorizing, SVG sprite generating, SVG to base64 data encoding, and more. These online applications work on any operating system with a web browser and don’t require additional software installation. It’s a fast and easy way to efficiently and effectively solve your SVG-related tasks!