Матрица Трансформации – примеры кода SVG
Масштабируемая векторная графика (SVG) – это язык XML для создания двумерной векторной и смешанной векторно-растровой графики. А матрица трансформации – это матрица, преобразующая один вектор в другой вектор в процессе умножения матрицы. Таким образом, это удобный инструмент для применения преобразований SVG, таких как трансляция, поворот, масштабирование и наклон. Матрицы трансформации основаны на линейной алгебре, которая предлагает математически элегантный способ выражения сложных преобразований. Эта математическая основа упрощает работу с трансформациями SVG для разработчиков и дизайнеров с математическим образованием.
Давайте подробнее посмотрим, как это работает!
Матрица трансформации
Матрица трансформации имеет размер 3x3 и объединяет преобразования перемещения, масштабирования, вращения и наклона. Вот что представляет собой каждый элемент:
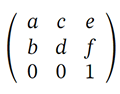
a – это может быть коэффициент масштабирования в направлении x, обычно обозначаемый как sx, или значение косинуса cos(α) угла поворота
b – это может быть tan(α) skewing factor в направлении y или синусоидальное значение sin(α) угла поворота
c – это может быть tan(α) skewing factor в направлении x или синусоидальное значение -sin(α) угла поворота
d – это может быть коэффициент масштабирования в направлении y, обычно обозначаемый как sy, или значение косинуса cos(α) угла поворота
e – сдвиг (трансляция) по оси x обычно обозначается как tx
f – сдвиг по оси Y обычно обозначается как ty
Матрица трансформации позволяет получить новые координаты точек объекта (x new, y new) в ходе преобразования путем умножения их на значения предыдущих координат (x prev, y prev):
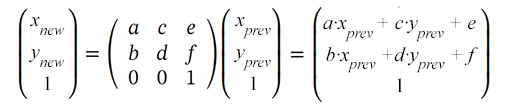
Объекты SVG можно изменить, используя свойство матрицы в transform атрибуте: transform=“matrix(a,b,c,d,e,f)”. Можно указать только первые 6 значений. Таким образом, вы предоставляете 6 значений функции матричного преобразования для установки трансляции, масштабирования, вращения и наклона.
Матрица трансляции – Translation Matrix
translation – это трансформация в SVG, которая перемещает все точки объекта на одинаковое расстояние по параллельным линиям. Это преобразование смещает начало системы координат элемента. Матрица трансляции (переноса, сдвига) выглядит следующим образом:
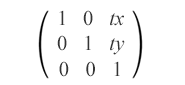
matrix(1,0,0,1,tx,ty)
Матрица трансляции объединяет значения tx и ty для перемещения элемента по горизонтали и вертикали. Она смещает объект на tx по оси X и на ty по оси Y.
Посмотрите на пример с исходным синим прямоугольником, который перемещается вдоль оси X (красный), оси Y (оранжевый) и обеих (зеленый):
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation by tx=30 -->
6 <circle cx="15" cy="15" r="10" stroke="red" transform="matrix(1 0 0 1 30 0)" />
7 <!-- vertical translation by by ty=25 -->
8 <circle cx="15" cy="15" r="10" stroke="orange" transform="matrix(1 0 0 1 0 25)" />
9 <!-- both horizontal and vertical translation by tx=30 and by ty=25 -->
10 <circle cx="15" cy="15" r="10" stroke="green" transform="matrix(1 0 0 1 30 25)" />
11 </g>
12</svg>Действие атрибута transform=“matrix(1,0,0,1,tx,ty)” означает изменение координат объекта по формуле:
x(new) = a·x(prev) + b·y(prev) +e = x(prev) + tx
y(new) = b·x(prev) + d·y(prev) +f = y(prev) + ty
В примере кода элемент <g> используется для группировки окружностей. Атрибут fill применяется внутри <g> ко всем фигурам один раз. Вот полученное изображение:

Матрица масштабирования – Scaling Matrix
Масштабирование – это преобразование SVG, которое увеличивает или уменьшает объект с использованием коэффициента масштабирования. Матрица масштабирования используется для равномерного или неравномерного масштабирования объектов по осям координат. sx и sy – коэффициенты масштабирования для осей x и y. Если sx и sy больше 1, объект будет увеличен; если они находятся между 0 и 1, объект будет уменьшен. Если для масштабных коэффициентов установлены разные значения, масштаб объекта будет неравномерным, что приведет к эффекту растяжения или сжатия.
Матрица масштабирования выглядит следующим образом:
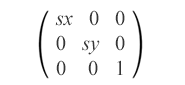
matrix(sx,0,0,sy,0,0)
Посмотрите на пример с исходным синим прямоугольником, который масштабируется равномерно и неравномерно относительно начала координат (0, 0) – рисунки a и b, и масштабируется равномерно относительно точки (10, 10) – рисунок c:
1<svg viewBox="0 0 400 300" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale is shown in fig.a -->
3 <g fill="none">
4 <rect x="10" y="10" width="20" height="20" stroke="blue" />
5 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, 0, 0)" />
6 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, 0, 0)" />
7 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 0, 0)" />
8 </g>
9 <!-- non-uniform scale is shown in fig.b -->
10 <g transform="translate(70)">
11 <rect x="10" y="10" width="20" height="20" fill="blue" />
12 <rect x="10" y="10" width="20" height="20" fill="red" transform="matrix(1.5, 0, 0, 2, 0, 0)" />
13 <rect x="10" y="10" width="20" height="20" fill="orange" transform="matrix(3, 0, 0, 2.5, 0, 0)" />
14 <rect x="10" y="10" width="20" height="20" fill="green" transform="matrix(0.7, 0, 0, 0.5, 0, 0)" />
15 </g>
16 <!-- uniform scale relative to point (10, 10) is shown in fig.c -->
17 <g fill="none" transform="translate(170)">
18 <rect x="10" y="10" width="20" height="20" stroke="blue" />
19 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, -5, -5)" />
20 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, -10, -10)" />
21 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 3, 3)" />
22 </g>
23</svg>Вот полученное изображение:
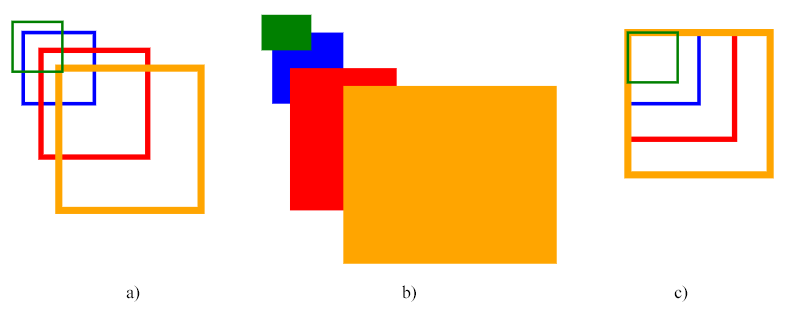
В приведенном выше коде используется матрица масштабирования. Первая группа прямоугольников на рисунке отображает пример равномерного масштабирования (рис. а), вторая группа иллюстрирует неравномерное масштабирование (рис. b), а третья группа прямоугольников (рис. c) показывает равномерное масштабирование относительно точки (10 , 10) – левый верхний угол синего (исходного) прямоугольника.
Примечание: Масштабирование выполняется относительно начала координат (0, 0) системы координат. Если точка (cx, cy) объекта SVG (относительно которого он нарисован) не находится в начале координат, применение трансформации масштабирования сместит положение объекта, что может создать впечатление перемещения. Эффект смещения прямоугольников мы видим на рисунках а и b.
Чтобы масштабироваться вокруг определенной точки (сx, сy), необходимо применить к масштабируемой фигуре дополнительное перемещение, чтобы поместить ее в эту точку (рис. c). Полная матрица трансформации, сочетающая перевод и масштабирование:
matrix(sx,0,0,sy,cx·(1-sx),cy·(1-sy))
Эта матрица будет правильно масштабировать объект вокруг точки поворота (cx, cy) без какого-либо перемещения. Коэффициенты cx·(1-sx) и cy·(1-sy) обеспечивают необходимое перемещение, чтобы гарантировать, что объект останется в исходном положении после масштабирования. Рассчитаем эти значения для красного прямоугольника (рис. c). Точкой поворота (cx, cy) в этом примере является (10, 10) – верхний левый угол синего (начального) прямоугольника:
cx·(1-sx)=10·(1-1,5)=10·(-0,5)=-5
cy·(1-sy)=10·(1-1,5)=10·(-0,5)=-5
Вы можете изменить размер SVG на C#, используя Aspose.SVG для .NET API. В статье
Масштабирование SVG — Примеры C# рассматриваются примеры C# для масштабирования SVG. Вы найдете случаи использования функции scale() в атрибуте transform, а также матрицы преобразования – matrix(a,b,c,d,e,f).
Матрица поворота – Rotation Matrix
Если вам нравится практиковаться в вычислении синусов и косинусов, вам сюда! Матрица вращения (поворота) выглядит следующим образом:
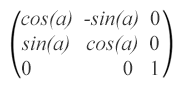
matrix(cos(α),sin(α),-sin(α),cos(α),0,0), где α – угол вокруг точки с координатами (0, 0) исходной системы координат.
Посмотрите на пример с исходным синим прямоугольником, который повернут на 90° (зеленый), 180° (серый), 270° (бирюзовый), -45° (красный) и 135° (оранжевый):
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- rotation around point with coordinates (0, 0) is shown in fig.a -->
3 <g>
4 <rect x="0" y="0" width="20" height="20" fill="blue" />
5 <rect x="0" y="0" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
6 <rect x="0" y="0" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
7 <rect x="0" y="0" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
8 <rect x="0" y="0" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
9 <rect x="0" y="0" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
10 <!-- rotation around point with coordinates (0, 0) is shown in fig.b -->
11 </g>
12 <g transform="translate(70)">
13 <rect x="5" y="5" width="20" height="20" fill="blue" />
14 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
15 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
16 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
17 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
18 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
19 </g>
20 <!-- rotation around point with coordinates (5, 5) is shown in fig.c -->
21 <g transform="translate(140)">
22 <rect x="5" y="5" width="20" height="20" fill="blue" />
23 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 10, 0)" />
24 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 10, 10)" />
25 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 10)" />
26 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, -2, 5)" />
27 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 12, 5)" />
28 </g>
29</svg>Примечание. Если мы используем положительное значение угла, то вращение будет по часовой стрелке, и наоборот, отрицательное значение угла дает нам вращение против часовой стрелки.
Результат вращения SVG можно увидеть на рисунке:
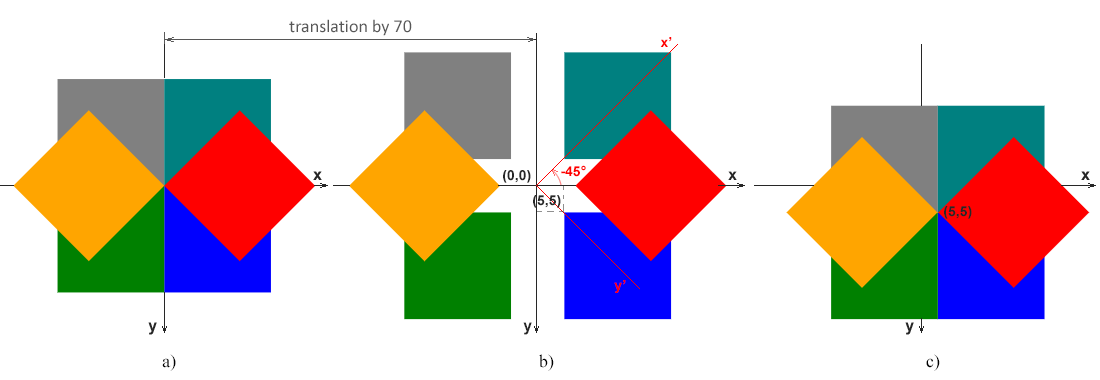
На рис. a показывает случай, когда верхний левый угол синего (начального) прямоугольника (0, 0) соответствует исходной точке системы координат (0, 0).
На рис. b иллюстрирует случай, когда верхний левый угол синего (начального) прямоугольника (5, 5) не совпадает с начальной точкой (0, 0). На этом рисунке показаны оси xy исходной системы координат, которые действительны для всех фигур a, b и c. Кроме того, красным показаны оси x’-y’ системы координат красного прямоугольника, который повернут на 45 градусов против часовой стрелки α=-45°. Отсюда ясно видно, что вращение прямоугольника сводится к вращению системы координат.
На рис. c показан случай, когда левый верхний угол синего (начального) прямоугольника (5, 5) не совпадает с начальной точкой системы координат (0, 0), но вращение происходит вокруг точки (5, 5).
Примечание. Следующая матрица будет вращать объект вокруг точки поворота (cx, cy):
matrix(cos(α), sin(α), -sin(α), cos(α), cx·(1-cos(α))+cy·sin(α), cy·(1-cos (α))-cx·sin(α))
Коэффициенты cx·(1-cos(α))+cy·sin(α) и cy·(1-cos(α))-cx·sin(α) обрабатывают необходимый перевод, чтобы гарантировать, что объект останется в исходном положении после вращения. Рассчитаем эти значения для красного прямоугольника (рис. c). Точкой поворота (cx, cy) в этом примере является (5, 5) – верхний левый угол синего (начального) прямоугольника, а угол красного прямоугольника равен -45°:
cos(-45°)=0,7071, sin(-45°)=-0,7071
cx·(1-cos(α))+cy·sin(α)=5·(1-0,7071)+5·(-0,7071)=-2
cy·(1-cos(α))-cx·sin(α)=5·(1-0,7071)-5·(-0,7071)=5
Вы можете поворачивать (вращать) SVG на C#, используя Aspose.SVG для .NET API. В статье
Поворот SVG — Примеры C# рассматриваются примеры C# для поворота SVG. Рассмотрены случаи использования функции rotate() в атрибуте transform и матрицы преобразования — matrix(a,b,c,d,e,f).
Матрица наклона – Skewing Matrix
Наклон (перекос) – это преобразование, которое поворачивает одну из осей системы координат элемента на определенный угол α по или против часовой стрелки. Элементы SVG можно искажать с помощью матрицы наклона, которая выглядит следующим образом:
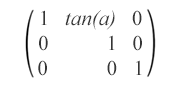
matrix(1,0,tan(α),1,0,0) – эта матрица наклона задает преобразование наклона вдоль оси x на α градусов.
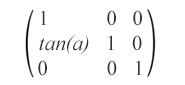
matrix(1,tan(α),0,1,0,0) – эта матрица наклона задает преобразование наклона вдоль оси Y на α градусов.
Вот пример круга с трансформацией наклона (перекоса):
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <circle cx="20" cy="20" r="10" stroke="blue" />
4 <!-- skew transformation along the x-axis by α=45° -->
5 <circle cx="20" cy="20" r="10" stroke="red" transform="matrix(1,0,1,1,0,0)" />
6 </g>
7 <g fill="none" transform="translate(70)">
8 <circle cx="20" cy="20" r="10" stroke="blue" />
9 <!-- skew transformation along the y-axis by α=45° -->
10 <circle cx="20" cy="20" r="10" stroke="orange" transform="matrix(1,1,0,1,0,0)" />
11 </g>
12</svg>Отрисованный пример выглядит так:

Примечание. Значение угла α указывает наклон SVG в градусах вдоль соответствующей оси. При использовании трансформации наклона вдоль оси x изменяется только координата x точек фигуры, но координата y остается неизменной. Преобразование наклона вдоль оси X придает вертикальным линиям вид, будто они повернуты на заданный угол. Координата x каждой точки изменяется на значение, пропорциональное заданному углу и расстоянию до начала координат.
Заключение
Матрица трансформации SVG – мощный инструмент для управления и анимации объектов в SVG. Она предоставляет универсальный способ применения перемещения, вращения, масштабирования и наклона к формам и элементам, позволяя создавать визуально динамичную и интерактивную графику. Матрица позволяет выполнять как отдельные, так и комбинированные трансформации, обеспечивая гибкость для достижения сложных и замысловатых визуальных эффектов. В этой статье мы рассмотрели только отдельные преобразования, но вскоре постараемся расширить наше руководство по рисованию SVG новыми статьями с более сложными примерами.
- Чтобы узнать больше и получить примеры кода SVG для вращения, масштабирования, перемещения и наклона графики SVG с использованием transform атрибута SVG, перейдите к статье
SVG Трансформации.
- Прочтите статью
Трансформации SVG – примеры C#, чтобы получить примеры кода C# для поворота, масштабирования, трансляции и наклона графики SVG с использованием библиотеки Aspose.SVG для .NET.
- Aspose.SVG предлагает бесплатные веб-приложения SVG для конвертации файлов SVG или изображений, объединения файлов SVG, векторизации изображений, генерации спрайтов SVG, кодирования данных SVG в base64 и многого другого. Эти онлайн-приложения работают в любой операционной системе с веб-браузером и не требуют установки дополнительного программного обеспечения. Это быстрый и простой способ эффективно и результативно решить ваши задачи, связанные с SVG!
