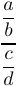5. Brüche, Binomialkoeffizienten und Mathematikstile
Ein weiteres häufiges Element in mathematischen Formeln sind Brüche und andere Konstruktionen, bei denen so etwas wie ein Zähler auf etwas wie einen Nenner gesetzt wird. Ein Beispiel für Letzteres sind Binomialkoeffizienten.
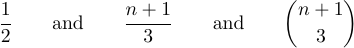
Sie können diese drei Formeln als angezeigte Gleichungen erhalten, indem Sie „$$1\over2$$“ und „$$n+1\over3$$ und $$\n+1\choose3$$“ eingeben.
Der Befehl „\over“ gilt für alles in der Formel, es sei denn, Sie schließen ihn in geschweifte Klammern in eine bestimmte Unterformel ein. In diesem Fall gilt „\over“ für alles in dieser Unterformel.

Sie können „\over“ nicht zweimal in derselben Unterformel verwenden, d. h. „a\over b\over 2“ eingeben. Stattdessen sollten Sie explizit angeben, was über was geht:

Es scheint, dass beide Formeln nicht sehr schön aussehen. In solchen Fällen ist es normalerweise am besten, Brüche in eine „Schrägstrichform“ umzuwandeln. Die letzten beiden Formeln sollten beispielsweise wie folgt eingegeben werden:
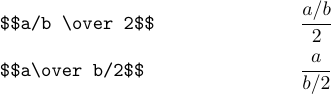
Hier sind komplexere Beispiele:
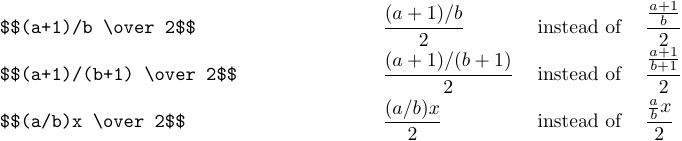
Wenn Sie sich die obigen Beispiele ansehen, ist Ihnen vielleicht aufgefallen, dass Buchstaben und andere Symbole manchmal kleiner werden, wenn sie in Brüchen stehen, genauso wie sie kleiner werden, wenn sie tiefgestellt oder hochgestellt sind. Lassen Sie uns nun über die Art und Weise sprechen, wie TeX die Größe von Symbolen auswählt. TeX verfügt über acht Stile, in denen Formeln behandelt werden können:
- Anzeigestil (für Formeln, die in einzelnen Zeilen angezeigt werden)
- Textstil (für in Text eingebettete Formeln)
- Skriptstil (für hochgestellte oder tiefgestellte Unterformeln)
- Skriptstil (für hochgestellte oder tiefgestellte Zeichen zweiter Ordnung) und vier „enge“ Stile, die fast gleich sind, außer dass tiefgestellte und hochgestellte Zeichen nicht so stark erhöht sind. Wir bezeichnen die acht Stile als D, D’, T, T’, S, S’, SS, SS’, wobei D für die Anzeige steht D’ ist ein enger Anzeigestil, T ist ein Textstil usw. TeX verwendet außerdem drei Größen zum Eingeben mathematischer Formeln: Textgröße, Skriptgröße und Skriptgröße.
Um eine Formel in Fließtext zu setzen, schließen Sie sie in „$…$“ ein; Dadurch entsteht die Formel im Stil T. Oder Sie können es in „$$…$$“ einschließen, um eine angezeigte Formel zu erhalten; Dadurch wird die Formel im Stil D angezeigt. Die Unterformeln einer Formel können unterschiedliche Stile haben. Sobald Sie den Stil kennen, können Sie die Schriftgröße bestimmen, die TeX verwenden wird:

Es gibt keinen „SSS“-Stil, da solche winzigen Symbole noch schlechter lesbar wären als die Scriptscript-Symbole.

Wenn beispielsweise „x^{a_b}“ im Stil D gesetzt werden soll, wird „a_b“ im Stil S und b im Stil SS gesetzt; Das Ergebnis ist
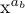
Wir haben bisher keinen Unterschied zwischen den Stilen D und T gesehen. Es gibt tatsächlich einen kleinen Unterschied in der Positionierung der Exponenten, obwohl in jedem Fall die Skriptgröße verwendet wird. Bei Brüchen gibt es jedoch einen großen Unterschied zwischen den Stilen D und T:

Wenn Sie also „$1\over2$“ (in einem Text) eingeben, erhalten Sie den Stil S über dem Stil S’. Wenn Sie jedoch „$$1\over2$$“ eingeben, wird in einer angezeigten Formel der Stil T über dem Stil T‘ angezeigt.
Schließlich ändert „\underline“ den Stil nicht. Mathe-Akzente und die Befehle \sqrt und \overline ändern nicht-cramped-Stile in ihre cramped-Gegenstücke, wobei cramped-Stile beibehalten werden.
Es kann vorkommen, dass Ihnen der Stil, den TeX nach seinen eigenen Regeln auswählt, nicht gefällt. Sie können den gewünschten Stil angeben, indem Sie \displaystyle oder \textstyle oder \scriptstyle oder \scriptscriptstyle eingeben; Der ausgewählte Stil gilt bis zum Ende der Formel oder Unterformel oder bis Sie einen anderen Stil auswählen. Beispielsweise ergibt „$$n+\scriptstyle n+\scriptscriptstyle n.$$“ die folgende Anzeige:
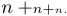
Es zeigt, dass auch das Pluszeichen kleiner wird, wenn sich der Stil ändert, und dass TeX in Skriptstilen kein Leerzeichen um + setzt.
Schauen wir uns ein anderes Beispiel an – einen Kettenbruch.
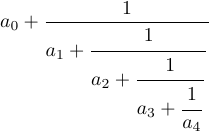
Sie können es durch Eingabe erhalten
1$$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$$Ohne „\strut“ und \displaystyle in dieser Formel wäre das Ergebnis anders:
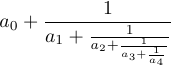
LaTeX definiert das Makro \frac, mit dem Sie Brüche mit einer anderen Syntax angeben können: „\frac{a}{b}“ entspricht „a\over b“ und „\frac12“ entspricht „1\over2“. `.
Es gibt eine weitere Operation „\atop“ in TeX, die wie „\over“ ist, außer dass sie die Bruchlinie nicht zeichnet:

Das LaTeX-Format definiert auch „\choose“, was wie „\atop“ ist, das Ergebnis jedoch in Klammern einschließt:
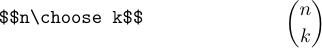
Es wird „\choose“ genannt, weil es eine übliche Schreibweise für den Binomialkoeffizienten ist, der angibt, wie viele Möglichkeiten es gibt, k Dinge aus n Dingen auszuwählen.
Die Befehle „\over“, „\atop“ und „\choose“ können nicht miteinander gemischt werden. Beispielsweise ist „$$n\choose k\over 2$$“ illegal. Sie müssen die Gruppierung verwenden, um entweder „$${n\choose k}\over2$$“ oder „$$n\choose{k\over2}$$“ zu erhalten.
TeX verfügt über den Befehl „\above“, der eine verallgemeinerte Version von „\over“ und „\atop“ ist. In diesem Befehl geben Sie die genaue Dicke der Linienlinie an, indem Sie „\above
1$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$erzeugt einen zusammengesetzten Bruch mit einer 1pt dicken Linie zwischen den Brüchen im Zähler und Nenner: