2. Anzeige und Ausrichtung für LaTeX-Gleichungen | LaTeX ausrichten

Das amsmath-Paket enthält eine Reihe von Umgebungsdefinitionen für die Eingabe angezeigter mathematischer Formeln. Sie können nach der Anzahl der Materiallinien (einzeln oder mehrfach) und nach der Anzahl der Ausrichtungspunkte klassifiziert werden.

In diesem Abschnitt verwenden wir den Begriff Gleichung folgendermaßen: um auf einen logisch eindeutigen Teil einer mathematischen Anzeige zu verweisen, der oft zur Referenz nummeriert und auch beschriftet ist (z. B. durch seine Nummer in Klammern). Solche Beschriftungen werden auch Tags genannt.

Die folgende Liste enthält die beliebtesten Anzeigeumgebungen. Gegebenenfalls haben sie Formen mit Sternchen versehen, in denen die Gleichungen nicht markiert sind.

„Gleichung“	Gleichung*	Eine Linie, eine Gleichung
mehrzeilig	multiline*	Eine nicht ausgerichtete mehrzeilige Gleichung, eine Gleichungsnummer
„sammeln“	sammeln*	Mehrere Gleichungen ohne Ausrichtung
ausrichten	align*	Mehrere Gleichungen mit mehreren Ausrichtungen
flalign	flalign*	Mehrere Gleichungen: horizontal gespreizte Form von „align“
„gespalten“		Eine einfache Ausrichtung innerhalb einer mehrzeiligen Gleichung

Alle Beispiele in diesem Kapitel sind so gesetzt, dass das Mathematikmaterial zentriert ist und die Gleichungsnummern (Tags) rechts stehen. Um die Positionierung zu visualisieren, stellen wir in der Ausgabe blaue vertikale Linien dar, die den linken und rechten Rand sowie die Mittellinie darstellen. Im LaTeX-Quellcode verwenden wir den Kommentar „% —–…“, um Zeilen, die in der Präambel des Dokuments platziert werden sollen, von denen zu trennen, die im Textkörper platziert werden sollen.

\usepackage[leqno]{amsmath}
% -------------------------------------------------------------------------------
\begin{equation} (a-b)^2 = a^2-2ab+b^2 \end{equation}
\[ \cos2\eta = \cos^2\eta-\sin^2\eta \]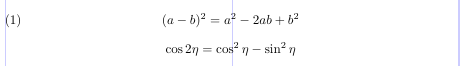

Wenn Sie die Mathematik in einem festen Einzug vom linken Rand und nicht zentriert in der Textspalte positionieren möchten, ist die Option „fleqn“ verfügbar. Sie können die Größe des Einzugs in der Präambel festlegen, indem Sie den Wert der Gummilänge „\mathindent“ festlegen. Sein Standardwert ist derselbe wie der Einzug einer Liste der ersten Ebene. Wenn Sie mit diesem Wert zufrieden sind, können Sie die Einstellung der „\mathindent“-Länge überspringen.

\usepackage[fleqn,reqno]{amsmath}
\setlength\mathindent{0.2in}
% -------------------------------------------------------------------------------
\begin{equation} (a-b)^2 = a^2-2ab+b^2 \end{equation}
\[ \cos2\eta = \cos^2\eta-\sin^2\eta \]

Hier muss die Option „reqno“ nicht übergeben werden (da dies die Standardeinstellung ist), aber sie überschreibt die Einstellungen der Dokumentklasse, sodass die Gleichungsnummer in jedem Fall nach rechts verschoben wird.

In Standard-LaTeX werden „&“ und „\“ für die Spalten- und Zeilentrennung innerhalb der angezeigten Ausrichtungen verwendet. Die Einzelheiten ihrer Verwendung ändern sich in den amsmath-Umgebungen.

2.1. Vergleich mit Standard-LaTeX

In einigen mehrzeiligen Anzeigeumgebungen können Sie Teile der Formel ausrichten. Im Vergleich zu den Standard-LaTeX-Umgebungen „eqnarray“ und „eqnarray*“ bieten die im Paket amsmath definierten Strukturen eine etwas andere und einfachere Möglichkeit, die Ausrichtungspunkte zu markieren. In Standard-LaTeX ähnelt „eqnarray*“ einer array-Umgebung mit „{rcl}“ als Präambel, was bedeutet, dass zwei „&“-Zeichen erforderlich sind, um die beiden Ausrichtungspunkte anzugeben. Im amsmath-Paket haben äquivalente Strukturen nur einen einzigen Ausrichtungspunkt (als ob array eine „{rl}“-Präambel hätte), sodass Sie links vom Symbol nur ein „&“-Zeichen einfügen müssen (normalerweise). eine Relation), die ausgerichtet werden soll.

Die „eqnarray“-Umgebung erzeugt abhängig von den Parametereinstellungen für array zusätzlichen Platz an den Ausrichtungspunkten. Die amsmath-Strukturen geben gleichzeitig feste Abstände vor. Der Unterschied wird am nächsten Beispiel deutlich. Dieselbe Gleichung wird mithilfe der Umgebungen „equation“, „align“ und „eqnarray“ gesetzt.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
x^2 + y^2 = z^2
\end{equation}
\begin{align}
x^2 + y^2 &= z^2 \\
x^3 + y^3 &< z^3
\end{align}
\begin{eqnarray}
x^2 + y^2 &=& z^2 \\
x^3 + y^3 &<& z^3
\end{eqnarray}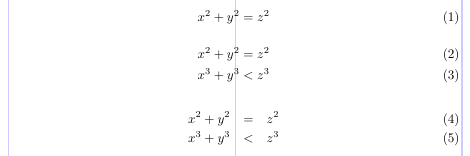

Beachten Sie, dass die Leerzeichen in der Umgebung „eqnarray“ für herkömmliche Standards des mathematischen Schriftsatzes zu groß sind. Wie in Standard-LATEX werden Zeilen in einer amsmath-Anzeige mit „\“ (oder dem Ende der Umgebung) markiert. Da der Zeilenumbruch in einer mathematischen Anzeige normalerweise ein tiefes Verständnis der Struktur der Formel erfordert, wird allgemein davon ausgegangen, dass er die Fähigkeiten heutiger Software übersteigt.

2.2. Eine einzelne Gleichung in einer Zeile

Eine einzelne Gleichung kann von der „Equation“-Umgebung erstellt werden. Ein Tag wird automatisch generiert und je nach verwendeter Option ganz links oder rechts platziert. Die Umgebung „equation*“ erzeugt dieselbe Gleichung ohne Tag. Standard-LaTeX verfügt ebenfalls über „Gleichung“, jedoch nicht über „Gleichung*“, da Letzteres der standardmäßig angezeigten Mathematikumgebung ähnelt.

Bemerkenswert ist, dass das Vorhandensein des Tags keinen Einfluss auf die Positionierung des Inhalts hat. Das Tag wird nach oben oder unten verschoben, falls in der einen Zeile nicht genügend Platz dafür ist: in die vorherige Zeile, wenn sich die Gleichungs-Tags links befinden, und in die nächste Zeile, wenn sich die Tags rechts befinden.

\usepackage[leqno]{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
n^2 + m^2 = k^2
\end{equation*}
\begin{equation}
n^p + m^p \neq k^p \qquad p > 2
\end{equation}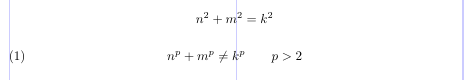

2.3. Eine einzelne Gleichung auf mehreren Zeilen ohne Ausrichtung

Eine Variante der „Equation“-Umgebung ist die „Multiline“-Umgebung. Es wird nur für Gleichungen verwendet, die nicht auf eine einzelne Zeile passen. Zur Markierung der Zeilenumbrüche muss das Zeichen „\“ verwendet werden, da diese nicht automatisch gefunden werden.

Die erste Zeile der „Mehrzeile“ wird an einer Einrückung vom linken Rand ausgerichtet und die letzte Zeile an derselben Einrückung vom rechten Rand. Der Wert der „\multlinegap“-Länge definiert die Größe dieser Einrückung.

Jede Zeile außer der ersten und letzten wird einzeln innerhalb der Anzeigebreite zentriert (es sei denn, die Option „fleqn“ wird verwendet). Wenn Sie jedoch den Befehl „\shoveleft“ oder „\shoveright“ innerhalb einer Zeile hinzufügen, wird diese Zeile zwangsweise nach links oder rechts verschoben.

Eine „mehrzeilige“ Umgebung hat ein einzelnes Tag, da es sich logischerweise um eine einzelne Gleichung handelt. Daher kann keine der einzelnen Zeilen durch die Verwendung von „\tag“ oder „\notag“ geändert werden. Das Tag wird, sofern vorhanden, rechts/links bündig in der letzten/ersten Zeile platziert, wenn die Option „reqno“/„leqno“ verwendet wird.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{multline}
\text{First line of a multline} \\
\text{Centered Middle line} \\
\shoveright{\text{A right Middle}} \\
\text{Another centered Middle} \\
\text{Yet another centered Middle} \\
\shoveleft{\text{A left Middle}} \\
\text{Last line of the multline}
\end{multline}

Das nächste Beispiel zeigt, wie sich „\multlinegap“ auf das Ergebnis auswirkt. Im ersten Fall reihen sich die „dy“s aneinander, was aussieht, als ob in der ersten Zeile der Gleichung ein Tag fehlt. Wenn „\multlinegap“ auf „0“ gesetzt ist, ändert sich der Abstand links von der zweiten Zeile aufgrund des Tags nicht, während die erste Zeile an den linken Rand verschoben wird, wodurch deutlich wird, dass es sich um eine einzelne Gleichung handelt .

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{multline} \tag{2}
\sum_{t \in \mathbf{T}} \int_a^t \biggl\lbrace \int_a^t f(t - x)^2 \, g(y)^2 \,dx \biggr\rbrace \,dy \\
= \sum_{t \notin \mathbf{T}} \int_t^a \biggl\lbrace g(y)^2 \int_t^a f(x)^2 \,dx \biggr\rbrace \,dy
\end{multline}
\setlength\multlinegap{0pt}
\begin{multline} \tag{2}
\sum_{t \in \mathbf{T}} \int_a^t \biggl\lbrace \int_a^t f(t - x)^2 \, g(y)^2 \,dx \biggr\rbrace \,dy \\
= \sum_{t \notin \mathbf{T}} \int_t^a \biggl\lbrace g(y)^2 \int_t^a f(x)^2 \,dx \biggr\rbrace \,dy
\end{multline}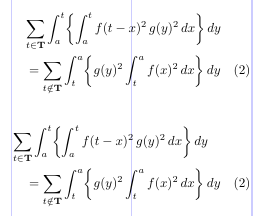

2.4. Eine einzelne Gleichung auf mehreren Zeilen mit Ausrichtung

Wenn Sie eine einzelne mehrzeilige Gleichung ausrichten müssen, steht Ihnen die „Split“-Umgebung zur Verfügung. Verwenden Sie einfach ein einzelnes „&“-Zeichen in jeder Zeile, um die Ausrichtungspunkte zu markieren.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
\begin{split}
(a + b)^4 &= (a + b)^2 (a + b)^2 \\
          &= (a^2 + 2ab + b^2)(a^2 + 2ab + b^2) \\
          &= a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
\end{split}
\end{equation}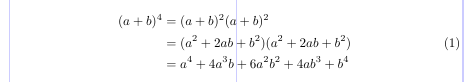

Eine „Aufteilung“ erzeugt selbst kein Gleichungs-Tag (die markierte Variante wird also nicht benötigt), da sie immer als Inhalt einer einzelnen Gleichung verwendet wird. Zu diesem Zweck können Sie es in eine äußere Umgebung bringen.

Standardmäßig ist das Tag (sowie jeder Teil der Gleichung außerhalb der „Teilung“) vertikal auf der Gesamthöhe des „geteilten“ Umgebungsmaterials zentriert. Dieses Verhalten entspricht der Option „centertags“. Wenn Sie die Option „tbtags“ angeben, wird das Tag in der letzten Zeile des „Split“ platziert, wenn sich das Tag rechts befindet, und in der ersten Zeile, wenn sich das Tag links befindet.

\usepackage[tbtags]{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
\begin{split}
(a - b)^3 &= (a - b) (a - b)^2 \\
          &= (a - b)(a^2 - 2ab + b^2) \\
          &= a^3 - 3a^2b + 3ab^2 - b^3
\end{split}
\end{equation}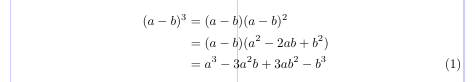

2.5. Gleichungsgruppen ohne Ausrichtung

Wenn Sie zwei oder mehr Gleichungen ohne Ausrichtung zwischen den Gleichungen in einer einzigen Anzeige zusammenfassen müssen, können Sie die Umgebung „gather“ verwenden. Es zentriert außerdem jede Gleichung separat innerhalb der Anzeigebreite und versieht sie bei Bedarf mit einem individuellen Tag. Jede Zeile einer „Sammlung“ ist logischerweise eine einzelne Gleichung.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather}
(a + b)^2 = a^2 + 2ab + b^2 \\
(a + b) \cdot (a - b) = a^2 - b^2
\end{gather}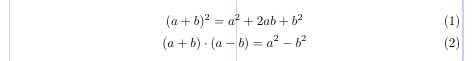

Möglicherweise müssen Sie die Gleichungsnummer für eine bestimmte Zeile unterdrücken. Der Befehl „\notag“, der in die logische Zeile eingefügt wird, ist die Antwort. Die „gather*“-Umgebung markiert Gleichungen überhaupt nicht.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather}
D(a,r) \equiv \{ z \in \mathbf{C} \colon |z - a| < r \} \notag \\
\operatorname{seg} (a, r) \equiv \{ z \in \mathbf{C} \colon \Im z < \Im a, \ |z - a| < r \} \\
C (E, \theta, r) \equiv \bigcup_{e \in E} c (e, \theta, r)
\end{gather}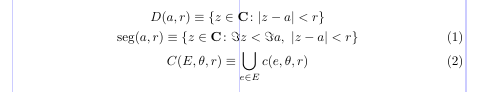

2.6. Gleichungsgruppen mit einfacher Ausrichtung

Wenn Sie mehr als eine Gleichung in einer einzigen Anzeige setzen und vertikal ausrichten müssen, kommt die „Align“-Umgebung zur Hilfe. Im einfachsten Fall verwenden Sie in jeder Zeile ein einzelnes „&“, um den Ausrichtungspunkt zu markieren.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align}
(a - b)^3 &= (a - b) (a - b)^2 \\
          &= (a - b)(a^2 - 2ab + b^2) \\
          &= a^3 - 3a^2b + 3ab^2 - b^3
\end{align}
\begin{align}
x^2 + y^2 &= 1 \\
        y &= \sqrt{1-x^2}
\end{align}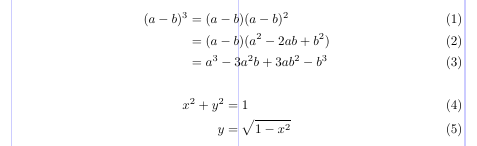

2.7. Mehrere Ausrichtungen

Eine „align“-Umgebung kann mehrere Ausrichtungspunkte definieren. Das Layout enthält so viele Spaltenpaare wie nötig und ähnelt einem array mit der „{rlrl…}“-ähnlichen Präambel. Unter der Annahme, dass es aus n solcher „rl“-Spaltenpaare besteht, beträgt die Anzahl der „&“ pro Zeile 2n - 1: eines für die Ausrichtung innerhalb jedes Spaltenpaares, was n ergibt; und n - 1 „&“ zum Trennen der Spaltenpaare.

Die „Align“-Umgebung verteilt das Material gleichmäßig über die Anzeigebreite. Wenn zusätzlicher Platz vorhanden ist, wird dieser gleichmäßig auf benachbarte Spaltenpaare und die beiden Anzeigeränder verteilt.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
This example has two column-pairs.
\begin{align} \text{Compare }
x^2 + y^2 &= 1 &                      x^3 + y^3 &= 1 \\
x              &= \sqrt {1-y^2}   &           x &= \sqrt[3]{1-y^3}
\end{align}
This example has three column-pairs.
\begin{align}
     x &= y        &        X &= Y      &   a &= b+c \\
    x' &= y'       &       X' &= Y'     &  a' &= b \\
x + x' &= y + y'   &   X + X' &= Y + Y' & a'b &= c'b
\end{align}

Das Layout des „flalign“ ist ähnlich, es gibt jedoch keinen Platz an den Rändern. Im nächsten Beispiel können Sie sehen, dass Gleichung (3) aufgrund dieser Tatsache auf eine einzelne Zeile passt (während Gleichung (2) immer noch nicht passt).

\usepackage{amsmath}
% -------------------------------------------------------------------------------
This example has two column-pairs.
\begin{flalign} \text{Compare }
x^2 + y^2 &= 1               &   x^3 + y^3 &= 1 \\
        x &= \sqrt {1-y^2}   &           x &= \sqrt[3]{1-y^3}
\end{flalign}
This example has three column-pairs.
\begin{flalign}
     x &= y        &        X  &= Y        &     a &= b+c \\
    x' &= y'       &       X'  &= Y'       &    a' &= b \\
x + x' &= y + y'   &   X + X'  &= Y + Y'   &   a'b &= c'b
\end{flalign}

In beiden Fällen kann der Mindestabstand zwischen Spaltenpaaren durch Ändern von „\minalignsep“ festgelegt werden. Der Standardwert ist „10pt“ und kann mit „\renewcommand“ geändert werden, da es sich um einen Makrobefehl und nicht um einen Längenparameter handelt. Das nächste Beispiel zeigt die Auswirkung der Änderung von „\minalignsep“.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
This example has two column-pairs.
\renewcommand\minalignsep{0pt}
\begin{align} \text{Compare }
x^2 + y^2 &= 1               &   x^3 + y^3 &= 1 \\
        x &= \sqrt {1-y^2}   &           x &= \sqrt[3]{1-y^3}
\end{align}
This example has three column-pairs.
\renewcommand\minalignsep{15pt}
\begin{flalign}
     x &= y        &        X  &= Y        &     a &= b+c \\
    x' &= y'       &       X'  &= Y'       &    a' &= b \\
x + x' &= y + y'   &   X + X'  &= Y + Y'   &   a'b &= c'b
\end{flalign}

Das nächste Beispiel veranschaulicht eine sehr häufige Verwendung von „align“. Beachten Sie die Verwendung von „\text“, um normalen Text innerhalb des mathematischen Materials zu erzeugen.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align}
     x &= y        &&   \text{by hypothesis} \\
    x' &= y'       &&   \text{by definition} \\
x + x' &= y + y'   &&   \text{by Axiom 1}
\end{align}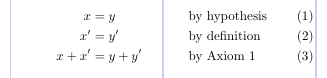

2.8. Unterbrechende Anzeigen: \intertext

Möglicherweise möchten Sie einen kleinen Textabschnitt zwischen die Zeilen einer Anzeigeausrichtung einfügen. Dies geschieht mit dem Befehl „\intertext“. Es ist sehr wichtig, dass alle Ausrichtungseigenschaften vom Text unberührt bleiben, während der Text selbst als normaler Absatz mit der Anzeigebreite gesetzt wird. Die Ausrichtung funktioniert nicht, wenn Sie die Anzeige einfach beenden und nach dem Text eine neue beginnen. Dieser Befehl muss immer unmittelbar auf einen „\“- oder „\*“-Befehl folgen.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align}
A_1 &= N_O (\lambda ; \Omega') - \phi ( \lambda ; \Omega') \\
A_2 &= \phi (\lambda ; \Omega') \phi (\lambda ; \Omega) \\
\intertext{and finally}
A_3 &= \mathcal{N} (\lambda ; \omega)
\end{align}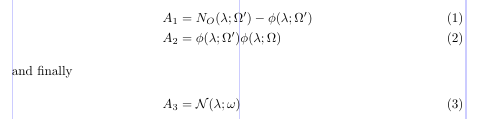

Die Wörter „und schließlich“ stehen außerhalb der Ausrichtung am linken Rand, aber alle drei Gleichungen sind ausgerichtet.

2.9. Gleichungsnummerierung und Tags

In LaTeX werden die Tags für Gleichungen normalerweise automatisch generiert und sind im Wesentlichen eine gedruckte Darstellung der LaTeX-Zähler-„Gleichung“. Dies erledigt LaTeX in drei Schritten: Festlegen des Werts des „Gleichungs“-Zählers; Formatieren des Tags; und an der richtigen Position ausdrucken.

Die ersten beiden Schritte sind eng miteinander verbunden, da der Zählerwert „Gleichung“ nur dann erhöht wird, wenn das entsprechende Tag automatisch gedruckt wird. Werfen wir einen Blick auf eine Anzeigeumgebung, die sowohl markierte als auch nicht markierte Formen hat. Nur die nicht markierte Form ändert den Wert des „Gleichungszählers“, da jede logische Gleichung automatisch markiert wird, während dies bei der markierten Form nicht der Fall ist. Wenn Sie das Setzen eines Tags für eine bestimmte logische Gleichung in der nicht markierten Form unterdrücken müssen, setzen Sie „\notag“ (oder „\nonumber“) vor dem „\“. Sie können die Standard-Tags auch durch solche Ihres eigenen Designs ersetzen, indem Sie den Befehl „\tag“ vor dem „\“ verwenden. Das Argument dieses Befehls kann ein beliebiger normaler Text sein, der in Klammern als Tag für diese Gleichung gesetzt wird.

Beachten Sie, dass das Erhöhen des Zählerwerts auch bei Verwendung von „\tag“ unterdrückt wird. Das bedeutet, dass die Standard-Tag-Einstellung nur optisch mit „\tag{\theequation}“ übereinstimmt; sie sind nicht gleichwertig. Die Sternform „\tag*“ setzt den Text in seinem Argument ohne die Klammern (und ohne andere Dinge, die sonst mit einer bestimmten Dokumentklasse hinzugefügt werden könnten).

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align}
x^2+y^2 &= z^2 \label{eq:A} \\
x^3+y^3 &= z^3 \notag \\
x^4+y^4 &= r^4 \tag{$*$} \\
x^5+y^5 &= r^5 \tag*{$*$} \\
x^6+y^6 &= r^6 \tag{\ref{eq:A}$'$} \\
A_1 &= N_0 (\lambda ; \Omega') - \phi ( \lambda ; \Omega') \\
A_2 &= \phi (\lambda ; \Omega') \, \phi (\lambda ; \Omega) \tag*{ALSO (\theequation)} \\
A_3 &= \mathcal{N} (\lambda ; \omega)
\end{align}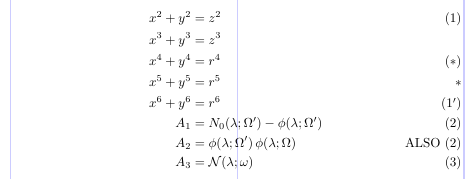

Beachten Sie, wie die Befehle \label und \ref verwendet werden, um eine Art „relative Nummerierung“ für Gleichungen bereitzustellen.

2.10. Untergeordnete Nummerierungssequenzen

Das amsmath-Paket unterstützt auch die sogenannte „Gleichungsunternummerierung“. Die Umgebung „subequations“ erzeugt Tags der Form (2a), (2b), (2c) usw. Dieses Nummerierungsschema basiert auf zwei normalen LaTeX-Zählern: „parentequation“ und „equation“. Alle getaggten Gleichungen innerhalb einer „subequations“-Umgebung verwenden dieses Schema.

Das folgende Beispiel zeigt, dass das Tag bis zu einem gewissen Grad neu definiert werden kann. Beachten Sie jedoch, dass die Neudefinition für „\theequation“ in der Umgebung „subequations“ platziert werden muss.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{subequations} \label{eq:1}
\begin{align}
           f &= g \label{eq:1A} \\
          f' &= g' \label{eq:1B} \\
\mathcal{L}f &= \mathcal{L}g \label{eq:1C}
\end{align}
\end{subequations}

\begin{subequations} \label{eq:2}
\renewcommand\theequation{\theparentequation\roman{equation}}
\begin{align}
           f &= g \label{eq:2A} \\
          f' &= g' \label{eq:2B} \\
\mathcal{L}f &= \mathcal{L}g + K \label{eq:2C}
\end{align}
\end{subequations}
Note the relationship between~\eqref{eq:1}
and~\eqref{eq:2}: only~\ref{eq:1C} and~\ref{eq:2C} differ.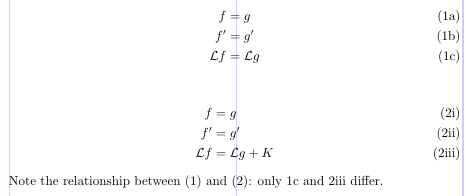

Die subequations-Umgebung muss außerhalb der von ihr betroffenen Anzeigen erscheinen. Sie sollte auch nicht in sich selbst verschachtelt sein. Der „Haupt“-Gleichungszähler wird bei jeder Verwendung dieser Umgebung erhöht. Ein \label-Befehl innerhalb der subequations-Umgebung, aber außerhalb einer einzelnen (logischen) Gleichung erzeugt ein \ref zur übergeordneten Nummer (z. B. zu 2 statt 2i).

2.11. Zurücksetzen des Gleichungszählers

Es ist üblich, Gleichungen innerhalb von Abschnitten oder Kapiteln mit Tags der Form (1.1), (1.2), …, (2.1), (2.2), … zu nummerieren. Das Paket amsmath bietet eine einfache Möglichkeit, dies mit der Deklaration „\numberwithin“ einzurichten.

Um beispielsweise Gleichungs-Tags einschließlich der Abschnittsnummer zu erhalten, wobei der Gleichungszähler für jeden Abschnitt automatisch zurückgesetzt wird, fügen Sie diese Deklaration in die Präambel ein: „\numberwithin{equation}{section}“.

Anhang A. Rendern von LaTeX-Gleichungen mit der Aspose.TeX-API

Jetzt schauen wir uns an, wie Sie mit der Aspose.TeX-API LaTeX-Gleichungen als eigenständige Zahlen erhalten.

Nehmen wir an, Sie benötigen eine Gleichung als Rasterbild, damit Sie sie in einer Nicht-TeX-Publikation (z. B. einer Webseite) verwenden können. Mit der Aspose.TeX-API können Sie dies wie folgt tun:

string equation = @"\begin{equation} (a-b)^2 = a^2-2ab+b^2 \end{equation}
\[ \cos2\eta = \cos^2\eta-\sin^2\eta \]";
Aspose.TeX.Features.PngMathRendererOptions options = new Aspose.TeX.Features.PngMathRendererOptions();
using (Stream stream = File.Open("your-file-name-and-path", FileMode.Create))
{
    new Aspose.TeX.Features.PngMathRenderer().Render(equation, stream, options, out System.Drawing.SizeF size);
    // Below is the short version for rendering with SVG
    // new Aspose.TeX.Features.SvgMathRenderer().Render(equation, stream, new Aspose.TeX.Features.SvgMathRendererOptions(), out System.Drawing.SizeF size);
}

Wie Sie sehen, ist die API auch in der Lage, eine LaTeX-Gleichung in eine SVG-Datei zu konvertieren. Und das war ein Beispiel für die Verwendung von Aspose.TeX für .NET. Unten finden Sie den entsprechenden Code für die Java-Version.

String equation = "\\begin{equation} (a-b)^2 = a^2-2ab+b^2 \\end{equation}\r\n" +
		"\\[ \\cos2\\eta = \\cos^2\\eta-\\sin^2\\eta \\]";
Size2D size = new Size2D.Float();
com.aspose.tex.PngMathRendererOptions options = new com.aspose.tex.PngMathRendererOptions();
final OutputStream stream = new FileOutputStream(Helper.getOutputFile(Path.combine(getCurrentPath(), "doc.png")));
try
{
    new com.aspose.tex.PngMathRenderer().render(equation, stream, options, size);
}
finally {
    stream.close();
}

Einzelheiten zur Verwendung von Renderer-Optionen finden Sie im Artikel zum Rendern von LaTeX-Matheformeln mit Aspose.TeX für .NET oder Aspose.TeX für Java. Aber einer davon ist für uns hier wichtig. Mit dieser Option können Sie die Präambel des LaTeX-Dokuments angeben, die Sie benötigen, um das gewünschte Ergebnis zu erhalten. (Im Folgenden präsentieren wir nur die C#-Version des Quellcodes.)

// The preamble for the very first example on this page
options.Preamble = @"\usepackage[leqno]{amsmath}";

Sie können diese Option auch verwenden, wenn Sie eine Gleichung in einem engeren Bereich anordnen müssen, als LaTeX „\textwidth“ standardmäßig definiert. Um dieses Ziel zu erreichen, haben Sie zwei Möglichkeiten:

// The preamble for the 2.7 examples
options.Preamble = @"\usepackage[textwidth=232pt]{geometry}
\usepackage{amsmath}";
// or
options.Preamble = @"\usepackage{amsmath}
\setlength{\textwidth}{232pt}";

In der Aspose.TeX-API wird standardmäßig die folgende Präambel verwendet. Wenn Sie also keine Optionen an das Paket amsmath übergeben oder die Standardeinstellung „\textwidth“ oder etwas anderes ändern müssen, müssen Sie die Präambel nicht in den Optionen des Renderers angeben :

\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}

Anhang B. Rendern von LaTeX-Gleichungen mit der Aspose LaTeX Equation-Web-App

Es gibt auch die LaTeX Equation Editor-Web-App, mit der Sie LaTeX-Gleichungen bearbeiten und anzeigen können. Sie können Ihre Gleichung in das Textfeld eingeben und auf die Schaltfläche Anzeigen klicken, um das Ergebnis anzuzeigen. Oder Sie können das Bedienfeld über dem Feld verwenden, um die Gleichung zu erstellen, indem Sie eine Unterausdruckskategorie und dann einen Unterausdruck auswählen und dann ggf. das Argument bearbeiten. Die Präambel und weitere Optionen finden Sie unterhalb des Feldes Formel.