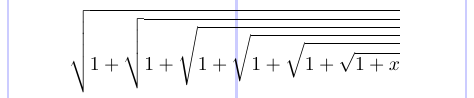5. Símbolos extensibles y ajustables
En LaTeX, existen ciertas características que permiten producir estructuras que pueden crecer hasta cualquier tamaño requerido. La composición tipográfica matemática necesita urgentemente dicha variabilidad. Discutiremos algunos aspectos del mismo en este artículo. Todos los comandos cubiertos en esta sección (a menos que se indique lo contrario) se proporcionan en LaTeX estándar.
5.1. Elipsis…
El paquete amsmath reemplaza (en casi todos los casos) todos esos \ldots, cdots, etc. del LaTeX estándar con el único comando \dots. Tanto la posición vertical de los puntos suspensivos como el espacio a su alrededor se seleccionan automáticamente dependiendo del tipo de símbolo que sigue a \puntos. Si el siguiente símbolo es, digamos, un signo más, los puntos aparecerán centrados; si es una coma, caerán en la línea de base. Siempre son tres puntos pero el espaciado es variable.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3A series $H_1, H_2, \dots, H_n$, a sum
4$H_1 + H_2 + \dots + H_n$, an orthogonal product
5$H_1 \times H_2 \times \dots \times H_n$.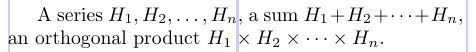
Sin embargo, cuando los puntos aparecen al final de una fórmula, el siguiente objeto será algo como \end o \) o $, y no le da a LaTeX ninguna pista sobre la posición de los puntos. En tal caso, debe ayudar usando \dotsc para puntos seguidos de comas, \dotsb para puntos seguidos de operador binario o símbolo de relación, \dotsm para puntos seguidos de puntos de multiplicación, \dotsi para puntos seguidos de integrales, o \dotso en cualquier otro caso.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3A series $H_1, H_2, \dotsc\,$, a sum
4$H_1 + H_2 + \dotsb\,$, an orthogonal product
5$H_1 \times H_2 \times \dotsm\,$, and an infinite
6integral: \[ \int_{H_1} \int_{H_2} \dotsi \;
7{-\Gamma}\, d\Theta \]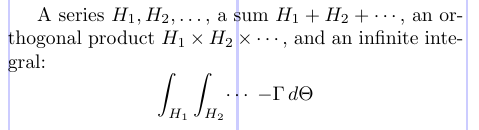
5.2. Símbolos que son extensibles horizontalmente.
Básicamente, LaTeX permite configurar cualquier comando de acento matemático para producir el glifo apropiado a partir de un rango de anchos siempre que las fuentes disponibles lo proporcionen. Sin embargo, en LaTeX estándar sólo existen dos de estos comandos: \widehat y \widetilde.
En el siguiente ejemplo, demostramos el uso de algunos comandos que producen construcciones similares a los acentos extensibles antes mencionados. Todos producen símbolos compuestos de la clase de matemáticas Ordinaria.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{align*}
4\widehat {\psi_\delta(t) E_t h}
5&= \widetilde {\psi_\delta(t) E_t h} \\
6\overline {\psi_\delta(t) E_t h}
7&= \underline {\psi_\delta(t) E_t h} \\
8\overbrace {\psi_\delta(t) E_t h}
9&= \underbrace {\psi_\delta(t) E_t h}
10& & \text{Do not change style} \\
11\overrightarrow {\psi_\delta(t) E_t h}
12&= \overleftarrow {\psi_\delta(t) E_t h}
13& & \text{Do not change style} \\[-3pt]
14& & & \text{without \textsf{amsmath}} \\
15\underrightarrow {\psi_\delta(t) E_t h}
16&= \underleftarrow {\psi_\delta(t) E_t h}
17& & \text{Do need \textsf{amsmath}} \\
18\overleftrightarrow {\psi_\delta(t) E_t h}
19&=\underleftrightarrow{\psi_\delta(t) E_t h}
20& & \text{Do need \textsf{amsmath}}
21\end{align*}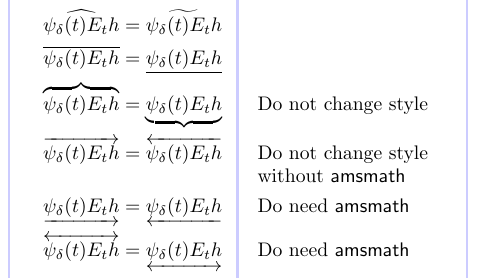
Aquí, “cambiar estilo” significa que el símbolo empleado se ve afectado por el estilo matemático en uso para que se vea bien cuando se use, por ejemplo, en fracciones o subíndice/superíndice. Aquellos que no cambien de estilo aparecerán correctamente sólo en el nivel superior de las fórmulas mostradas.
5.3. Símbolos que son extensibles verticalmente.
La extensibilidad vertical es mucho más amplia. La siguiente tabla enumera todos los símbolos que son extensibles verticalmente.
Símbolos verticalmente extensibles
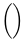 | ( ) | 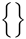 | \{ \} |  | \lVert \rVert |
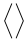 | \langle \rangle | 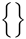 | \lbrace \rbrace |  | \lvert \rvert |
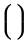 | \lgroup \rgroup |  | [ ] | 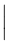 | ` |
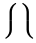 | \lmoustache \rmoustache |  | \lbrack \rbrack | 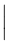 | \vert |
 | \Downarrow | 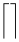 | \lceil \rceil | 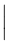 | \arrowvert |
 | \Uparrow | 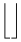 | \lfloor \rfloor | 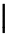 | \bracevert |
 | \Updownarrow | 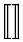 | \llbracket \rrbracket | 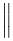 | \Arrowvert |
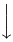 | \downarrow |  | / | 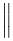 | | |
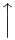 | \uparrow |  | \backslash | 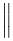 | \Vert |
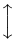 | \updownarrow | . | 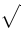 | \sqrtsign |
Los símbolos en cursiva requieren el paquete
amsmatho, si se escriben además en negrita, el paquetestmaryrd. Un punto (.) no es en sí mismo un símbolo extensible, pero se puede utilizar para producir un delimitador “invisible”. El símbolo\sqrtsignno se puede utilizar con\left,\righto\middle.
Sinónimos: [ -
\lbrack,[; ] -\rbrack,]; { -\lbrace,\{; } -\rbrace,\}; | -\vert,|; || -\Vert,\|.
Estos símbolos se vuelven extensibles sólo en ciertos usos. Deberán basarse en la siguiente construcción:
1\left <ext-Open> <sub-formula> \right <ext-Close>Si LaTeX utiliza el programa eTeX, también puede utilizar estos símbolos extensibles con
\middle.
Aquí <ext-Open> y <ext-Close> pueden ser cualquiera de los símbolos (excepto \sqrtsign) enumerados en la tabla anterior. Deben ser símbolos que se hayan configurado para ser extensibles como se describe en
fntguide. Por lo tanto, debe estar disponible un símbolo que represente la ausencia de un glifo real. Sucedió que este símbolo, también conocido como delimitador nulo, es el punto (.). Los tamaños de los glifos reales para componer un símbolo extensible se eligen para que se ajusten a la altura y profundidad de la subfórmula que se encuentra entre ellos.
El símbolo radical \sqrtsign crece tanto vertical como horizontalmente para adaptarse al tamaño de su argumento. En LaTeX, preferirías usar el comando \sqrt para obtener este símbolo.
1\[
2 \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 +
3 \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 + x}}}}}}
4\]