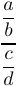5. Fracciones, coeficientes binomiales y estilos matemáticos.
Otra cosa común que puedes encontrar en las fórmulas matemáticas son las fracciones y otras construcciones en las que algo como un numerador se coloca encima de algo como un denominador. Un ejemplo de esto último son los coeficientes binomiales.
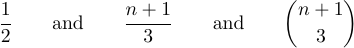
Puede obtener estas tres fórmulas como ecuaciones mostradas escribiendo $$1\over2$$ y $$n+1\over3$$ y $$\n+1\choose3$$.
El comando \over se aplica a todo lo que está en la fórmula a menos que lo incluya entre llaves en una subfórmula específica, en cuyo caso \over se aplica a todo lo que está en esa subfórmula.

No puede usar \over dos veces en la misma subfórmula, es decir, escriba a\over b\over 2. En su lugar, deberías especificar explícitamente qué incluye qué:

Parece que ambas fórmulas no pintan muy bien. En tales casos, suele ser mejor convertir las fracciones a una “forma barrada”. Por ejemplo, las dos últimas fórmulas deben escribirse de la siguiente manera:
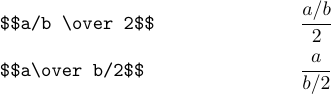
Aquí hay ejemplos más complejos:
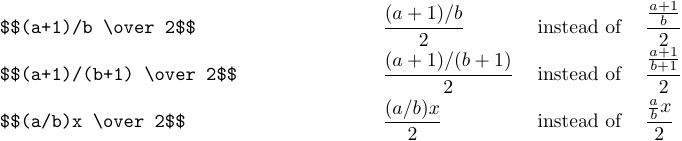
Al observar los ejemplos anteriores, es posible que hayas notado que las letras y otros símbolos a veces se hacen más pequeños cuando aparecen en fracciones, del mismo modo que se hacen más pequeños cuando están en subíndices o superíndices. Hablemos ahora de la forma en que TeX elige los tamaños de los símbolos. TeX tiene ocho estilos en los que puede tratar fórmulas:
- estilo de visualización (para fórmulas que se muestran solas en líneas)
- estilo de texto (para fórmulas incrustadas en texto)
- estilo de escritura (para subfórmulas utilizadas como superíndices o subíndices)
- estilo scriptscript (para superíndices o subíndices de segundo orden) y cuatro estilos “estrechos” que son casi iguales excepto que los subíndices y superíndices no se elevan tanto. Nos referiremos a los ocho estilos como D, D’, T, T’, S, S’, SS, SS’, donde D es visualización estilo, D’ es un estilo de visualización reducido, T es un estilo de texto, etc. TeX también usa tres tamaños para escribir fórmulas matemáticas: tamaño de texto, tamaño de escritura y tamaño de escritura.
Para componer una fórmula en texto en ejecución, encierrela en $...$; esto produce la fórmula en estilo T. O puede encerrarlo entre $$...$$ para obtener una fórmula mostrada; esto muestra la fórmula en estilo D. Las subfórmulas de una fórmula pueden tener diferentes estilos. Una vez que conozca el estilo, podrá determinar el tamaño de letra que utilizará TeX:

No existe el estilo “SSS” ya que símbolos tan pequeños serían incluso menos legibles que los de scriptscript.

Por ejemplo, si x^{a_b} se va a escribir con el estilo D, a_b se escribirá con el estilo S y b con el estilo SS; el resultado es
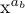
No hemos visto ninguna diferencia entre los estilos D y T todavía. En realidad, existe una ligera diferencia en la posición de los exponentes, aunque en cada caso se utiliza el tamaño de escritura. Pero hay una gran distinción entre los estilos D y T en el caso de fracciones:

Entonces, si escribe $1\over2$ (en un texto) obtendrá el estilo S sobre el estilo S’. Pero si escribe $$1\over2$$ obtendrá el estilo T sobre el estilo T’ en una fórmula mostrada.
Finalmente, \underline no cambia el estilo. Los acentos matemáticos y los comandos \sqrt y \overline cambian los estilos libres a sus contrapartes apretados que conservan los estilos apretados.
Puede suceder que no te guste el estilo que TeX selecciona según sus propias reglas. Usted es libre de especificar el estilo deseado escribiendo \displaystyle o \textstyle o \scriptstyle o \scriptscriptstyle; el estilo seleccionado se aplicará hasta el final de la fórmula o subfórmula, o hasta que seleccione otro estilo. Por ejemplo, $$n+\scriptstyle n+\scriptscriptstyle n.$$ produce la siguiente visualización:
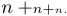
Muestra que el signo más también se hace más pequeño a medida que cambia el estilo, y que TeX no coloca espacios alrededor de + en los estilos de escritura.
Veamos otro ejemplo: una fracción continua.
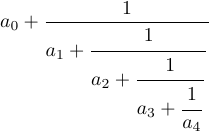
Puedes obtenerlo escribiendo
1$$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$$Sin \strut y \displaystyle en esta fórmula, el resultado sería diferente:
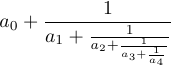
LaTeX define la macro \frac que le permite especificar fracciones usando otra sintaxis: \frac{a}{b} es equivalente a a\over b y \frac12 es equivalente a 1\over2 .
Hay otra operación \atop en TeX, que es como \over excepto que no dibuja la línea de fracción:

El formato LaTeX también define \choose, que es como \atop pero encierra el resultado entre paréntesis:
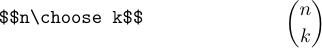
Se llama \choose porque es una notación común para el coeficiente binomial que indica cuántas maneras hay de elegir k cosas entre n cosas.
Los comandos \over, \atop y \choose no se pueden mezclar entre sí. Por ejemplo, $$n\choose k\over 2$$ es ilegal. Debe utilizar la agrupación para obtener $${n\choose k}\over2$$ o $$n\choose{k\over2}$$.
TeX tiene el comando \above que es una versión generalizada de \over y \atop. En este comando, usted especifica el grosor exacto de la regla de línea escribiendo \above<dimen>. Por ejemplo,
1$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$producirá una fracción compuesta con una regla de 1 punto de espesor entre las fracciones en el numerador y el denominador: