9. Símbolos en fórmulas matemáticas
Las tablas de este artículo enumeran la amplia gama de símbolos matemáticos proporcionados por los paquetes AMS-LATEX, incluidos comandos para acceder a cada símbolo. También incluyen los símbolos complementarios de la fuente St Mary Road diseñada por Allan Jeffrey y Jeremy Gibbons. Este paquete amplía las colecciones de fuentes de símbolos Computer Modern y AMS y normalmente debe cargarse además de amssymb, pero siempre después de él. Proporciona símbolos adicionales para campos como programación funcional, álgebra de procesos, teoría de dominios, lógica lineal y muchos más.
Las tablas indican qué paquetes adicionales deben cargarse para usar cada comando de símbolo. Los símbolos con nombres de comandos en negro están disponibles en LaTeX estándar. Los símbolos con nombres de comandos en azul requieren cargar amsmath, amssymb o stmaryrd. Si es necesario, se proporciona una clasificación adicional mediante marcas: (StM) significa un símbolo de stmaryrd cuando la tabla también contiene símbolos de otros paquetes; (kernel) marca símbolos que están disponibles en LaTeX estándar pero solo combinando dos o más glifos, mientras que existe un solo glifo en el paquete indicado; y (var) marca “Símbolos alfabéticos” (de tipo \mathalpha) que cambian de apariencia cuando se usan dentro del alcance de un
identificador del alfabeto matemático.
9.1. Clases de matemáticos símbolos LaTeX
La clasificación principal de los símbolos matemáticos está relacionada con su significado en el uso técnico. En tipografía matemática, esta clasificación define el diseño de la fórmula. En particular, el formateador matemático de TeX ajusta el espacio horizontal a cada lado de cada símbolo según su clase matemática. Esta clasificación también hace algunas distinciones más finas, por ejemplo, entre acentos y símbolos simples y al dividir la enorme lista de símbolos de Relación en varias tablas.
La configuración para matemáticas coloca cada símbolo en una de estas clases: Ordinario (Ord), Operador (Op), Binario (Bin), Relación (Rel), Apertura (Abrir), Cierre (Cerrar), o Puntuación (Punct). La clase del símbolo se puede cambiar explícitamente usando los comandos \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathopen y \mathpunct. En el siguiente ejemplo, \# y \top (ambos Ord por defecto) se cambian a Rel y Op.
1\usepackage[fleqn]{amsmath}
2\[ a \# \top _x^\alpha x^\alpha_b \]
3\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]
Además de las clases anteriores, ciertas subfórmulas (principalmente fracciones y aquellas producidas por \left y \right) forman una clase llamada Inner, que está disponible explícitamente a través del comando \mathinner.
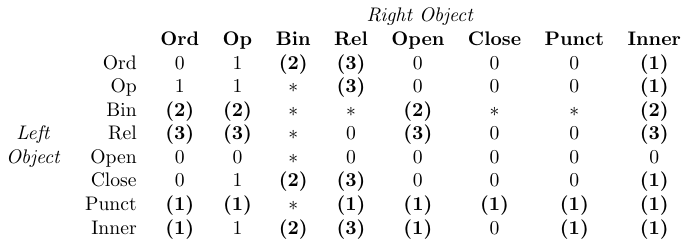
En la tabla, “0” significa “sin espacio”, “1” significa
\thinmuspace, “2” significa\medmuskip, “3” significa\thickmuskip, “*” significa “imposible”. Las entradas en negrita significan que no se agrega el espaciado correspondiente en los estilos de escritura matemática.
TeX maneja el espaciado dentro de las fórmulas simplemente identificando la clase de cada objeto en una fórmula y luego agregando espacio entre cada par de objetos adyacentes como se define en la tabla anterior. Esta tabla está codificada en las rutinas de composición tipográfica matemática de TeX y, por lo tanto, los paquetes de macros no pueden modificarla.
Un símbolo Binario se convierte en un símbolo Ordinario siempre que no esté precedido ni seguido por símbolos de naturaleza compatible con una operación binaria. Por eso algunas entradas de la tabla están marcadas como imposibles. Por ejemplo, $+x$ da +x (un más unario) y no + x. Este último puede ser producido por ${}+x$.
Considere la siguiente fórmula (los valores predeterminados se cambian para mostrar los espacios agregados con mayor claridad):
1thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[
4a - b = -\max \{ x , y \}
5\]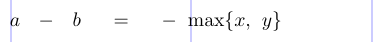
TeX identifica los objetos como Ord, Bin, Ord, etc., y luego inserta espacios de la siguiente manera:
1 A - b = - \max \{ x , y \}
2Ord \: Bin \: Ord \; Rel \; Ord \, Op Open Ord Punct \, Ord CloseEl signo menos delante de \max se convierte en Ordinario porque un Binario no puede seguir una Relación.
En una construcción “\left...\right”, toda la subfórmula delimitada por la construcción se convierte en un único objeto de clase Inner. Por el contrario, comandos como \Bigl y \Bigr producen símbolos individuales de las clases Apertura y Cierre, respectivamente. La diferencia entre ellos se revela en la tabla de espaciado anterior. Aunque pueden dar como resultado delimitadores de igual tamaño vertical, pueden surgir diferencias de espaciado dependiendo de los objetos adyacentes en la fórmula. Por ejemplo, Ordinario seguido de Apertura no tiene espacio, mientras que Ordinario seguido de Interior está separado por un espacio fino. Los espacios dentro de la subfórmula dentro de una construcción “\left...\right” se crean como se esperaba, comenzando con un símbolo de Apertura y terminando con un símbolo de Cierre.
1\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]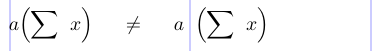
En resumen, es mejor comprobar que un símbolo pertenece a la clase deseada, en lugar de simplemente buscarlo en las tablas siguientes.
9.2. Letras, números y otros símbolos ordinarios
Las letras latinas ASCII sin acentos y los dígitos de los números arábigos se denominan “símbolos alfabéticos”. La fuente en la que están escritos puede variar. En las fórmulas matemáticas, la fuente predeterminada para las letras latinas es cursiva, mientras que para los dígitos árabes es vertical/romana. Los símbolos alfabéticos son todos de la clase Ordinario.
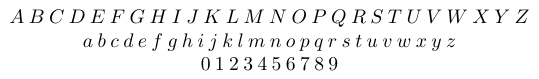
A diferencia de las letras latinas, las letras matemáticas griegas ya no están estrechamente relacionadas con los glifos utilizados para componer texto griego normal. Debido a una curiosa casualidad del siglo XVIII, en la principal tradición europea de tipografía matemática, la fuente predeterminada para las letras griegas minúsculas en las fórmulas matemáticas es cursiva, mientras que para las letras griegas mayúsculas es vertical/romana. (En física y química, por ejemplo, las tradiciones tipográficas son ligeramente diferentes).
Las letras mayúsculas griegas en las primeras filas de la siguiente tabla también son símbolos alfabéticos cuya fuente varía, siendo la predeterminada vertical/romana. Hay letras griegas mayúsculas, cada una de las cuales tiene la misma apariencia que alguna letra latina (por ejemplo, A y Alpha, B y Beta, K y Kappa, O y *Omicron *). Estas letras no están presentes en la tabla. Por la misma razón, no hay ómicrón en minúsculas. En la práctica, las letras griegas que parecen letras latinas no se utilizan en fórmulas matemáticas.

Los símbolos en azul requieren el paquete
amssymb. (var) indica un símbolo alfabético variable.
La siguiente tabla enumera otros símbolos en forma de letras de la clase Ordinario. Las primeras cuatro son letras hebreas.

Los símbolos en azul requieren el paquete
amssymb.
La siguiente tabla enumera los símbolos restantes de la clase Ordinario, incluyendo algunos signos de puntuación comunes. Se comportan como letras y dígitos, por lo que nunca tienen espacio adicional a su alrededor.

Los símbolos en azul requieren el paquete
amssymbo, si están marcados con (StM), el paquetestmaryrd.
Tenga en cuenta que el signo de exclamación, el punto y el signo de interrogación no se tratan como signos de puntuación en las fórmulas.
Sinónimos: negación lógica -
\lnot,\neg;|-\vert,|;||-\Vert,\|.
Un error común es utilizar estos símbolos directamente como operadores binarios o símbolos de relación, sin utilizar un comando de símbolo matemático correctamente definido para ese tipo. Por lo tanto, si usa comandos como \#, \square o \&, verifique cuidadosamente que obtenga los espacios entre símbolos correctos o, mejor aún, defina su propio comando de símbolo.
1\usepackage[fleqn]{amsmath} \usepackage{amssymb}
2\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
3\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
4% -------------------------------------------------------------------------------
5\[ a \neg b \qquad x \square y + z \]
6\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
7\[ a \bneg b \qquad x \rsquare y + z \]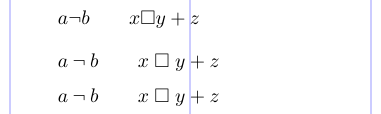
El comando \DeclareMathSymbol se utiliza para declarar su propio nombre de símbolo.
1\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}El primer argumento es el nombre del comando elegido. El segundo argumento es uno de los comandos correspondientes a la clase de símbolo. El tercer argumento identifica la fuente del símbolo de la que se debe obtener el símbolo. El cuarto argumento proporciona la posición del símbolo en la codificación de fuente, ya sea un valor decimal, octal o hexadecimal. Los valores correctos para los argumentos se pueden encontrar más fácilmente mirando las definiciones en el archivo amssymb.sty o fontmath.ltx (para los símbolos principales). Por ejemplo, buscamos \neq y \square, reemplazamos \mathord en cada caso y finalmente le dimos un nuevo nombre al símbolo resultante.
9.3. Acentos matemáticos
La siguiente tabla enumera los comandos de acento disponibles en las fórmulas. La mayoría de ellos están definidos en TeX estándar. Consulte aquí para obtener información sobre acentos extensibles. Cuando agrega un acento matemático a un símbolo, el resultado es un símbolo de clase Ordinario.
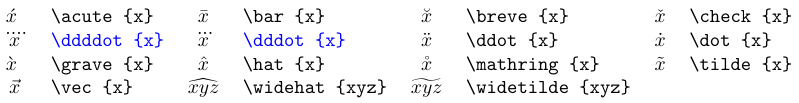
Los acentos en azul requieren el paquete
amsmath.
Los dos últimos acentos están disponibles en una variedad de anchos, y se utiliza automáticamente el más grande que sea adecuado.
1\usepackage{amstext}
2% -------------------------------------------------------------------------------
3\[ a = b \text{ but } a \tilde{=} b
4\text{ which is not } a \mathrel{\tilde{=}} b \]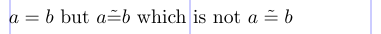
Otras formas de colocar símbolos sobre símbolos de Relación se muestran
aquí. Al agregar un acento a i o j en fórmulas matemáticas, es mejor usar las variantes sin puntos \imath y \jmath.
9.4. Símbolos del operador binario
Hay más de 100 símbolos de clase Binario entre los que elegir. La mayoría de ellos se enumeran en la siguiente tabla. Algunos de ellos también están disponibles como símbolos de Relación, aunque con nombres diferentes.

Los símbolos en azul requieren el paquete
amssymbo, si están marcados con (StM), el paquetestmaryrd.
Los triángulos izquierdo y derecho también están disponibles como símbolos de Relación.
El paquete
stmaryrdcambia de manera confusa los símbolos Binarios\bigtriangleupy\bigtriangledownen Operadores, dejando solo los sinónimos\varbigtriangleupy\varbigtriangledownpara las formas de operador Binario.
El paquete amssymb ofrece algunos símbolos de cuadro para usar como operadores binarios; stmaryrd agrega muchos más. Vea la siguiente tabla.

Todos los símbolos requieren el paquete
amssymbo, si está marcado con (StM), el paquetestmaryrd.
Puede cargar el paquete stmaryrd con la opción heavycircles. Como resultado, cada comando de símbolo de círculo de la siguiente tabla que comienza con \var intercambia su definición con el comando correspondiente sin “var”; por ejemplo, el símbolo \varodot se convierte en \odot y viceversa.

Los símbolos en azul requieren el paquete
amssymbo, si están marcados con (StM), el paquetestmaryrd.
La opción
heavycirclesdel paquetestmaryrdafecta a todos los comandos que comienzan con\vary sus variantes normales.
9.5. Símbolos de relación
La clase de símbolos binarios Relación es incluso mayor que la de los operadores Binarios. La siguiente tabla enumera los símbolos de igualdad y orden. Se puede colocar una barra diagonal en cualquier símbolo de Relación precediéndolo con el comando \not. El símbolo negado representa el complemento (o negación) de las relaciones.
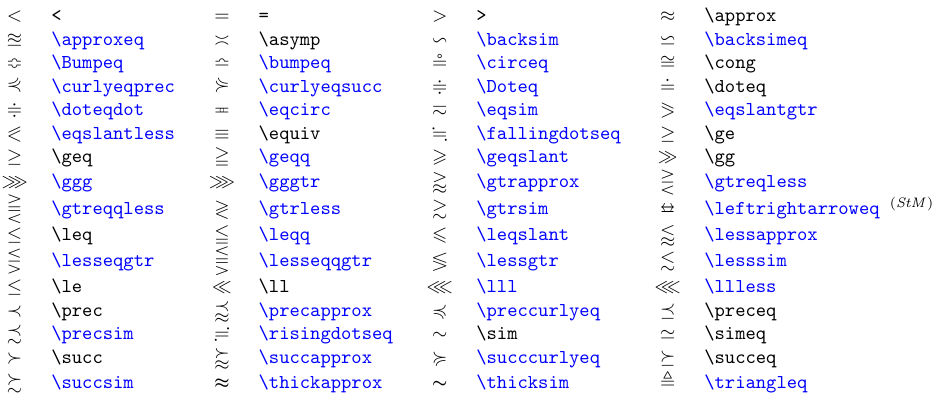
Los símbolos en azul requieren el paquete
amssymbo, si está marcado (StM), el paquetestmaryrd.
1$ u \not< v$ or $a \not\in \mathbf{A} $
Este método genérico de negar un símbolo de Relación no siempre da buenos resultados, especialmente con símbolos más grandes, porque la barra siempre tendrá el mismo tamaño, posición e inclinación. Debido a este hecho, también están disponibles algunos “símbolos negados” especialmente diseñados. Vea la lista en la siguiente tabla.

Los símbolos en azul requieren el paquete
amssymb.
Si hay una opción disponible, normalmente es preferible utilizar los glifos especialmente diseñados. Para ver por qué, compare los símbolos en el siguiente ejemplo.
1\usepackage{amssymb}
2% -------------------------------------------------------------------------------
3$ \not\leq \ \not\succeq \ \not\sim $ \par
4$ \nleq \ \nsucceq \ \nsim $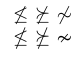
La siguiente tabla enumera los símbolos de Relación para conjuntos e inclusiones.

Los símbolos en azul requieren el paquete
amssymbo, si están marcados con (StM), el paquetestmaryrd.
Y ahora negaciones de los símbolos de Relación para conjuntos e inclusión.

Los símbolos en azul requieren el paquete
amssymb.
La siguiente tabla enumera los símbolos de Relación en forma de flecha. Algunas construcciones de flechas extensibles que producen símbolos compuestos de Relación se describen aquí.

Los símbolos en azul requieren el paquete
amssymbo, si están marcados con (StM), el paquetestmaryrd.
Y aquí están los símbolos de Relación negados en forma de flecha.

Los símbolos en azul requieren el paquete
amssymb.
Hay otros elementos (además de \not usado para negar símbolos generales de Relación) que fueron especialmente diseñados para negar o extender símbolos tipo flecha. Vea la siguiente tabla.
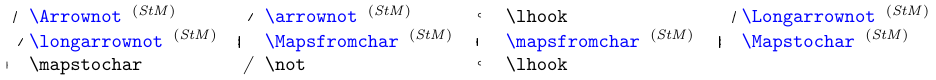
Los símbolos en azul requieren el paquete
stmaryrd.
Estos símbolos se utilizan para combinar, principalmente con flechas; por ejemplo,
\longarrownot\longleftarrow.
Utilice
\joinrelpara “pegar” símbolos relacionales, por ejemplo,\lhook\joinrel\longrightarrow.
Las dimensiones de estos símbolos los hacen inadecuados para otros usos.
1\usepackage{stmaryrd}
2% -------------------------------------------------------------------------------
3$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$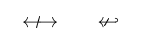
Finalmente, a continuación se muestran otros símbolos diversos de Relación.

Los símbolos de Relación en azul requieren el paquete
amssymb.
\thereforees un símbolo de Relación, por lo que su espaciado puede no ser el esperado en usos comunes.