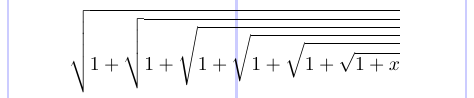5. Symboles extensibles et réglables | Manuel LaTeX

Dans LaTeX, certaines fonctionnalités permettent de produire des structures pouvant atteindre n’importe quelle taille requise. La composition mathématique a cruellement besoin d’une telle variabilité. Nous en aborderons certains aspects dans cet article. Toutes les commandes couvertes dans cette section (sauf indication contraire) sont fournies par LaTeX standard.

5.1. Ellipse…

Le package amsmath remplace (dans presque tous les cas) tous ces \ldots, cdots, etc. de LaTeX standard par la seule commande \dots. La position verticale des points de suspension et l’espace qui l’entoure sont automatiquement sélectionnés en fonction du type de symbole suivant \dots. Si le symbole suivant est, par exemple, un signe plus, les points apparaîtront centrés ; s’il s’agit d’une virgule, ils tomberont sur la ligne de base. Il s’agit toujours de trois points mais l’espacement est variable.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3A series $H_1, H_2, \dots, H_n$, a sum
4$H_1 + H_2 + \dots + H_n$, an orthogonal product
5$H_1 \times H_2 \times \dots \times H_n$.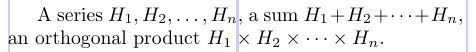

$Ellipse avec espacement déterminé automatiquement$

Cependant, lorsque les points apparaissent à la fin d’une formule, l’objet suivant sera quelque chose comme \end ou \) ou $, et cela ne donne à LaTeX aucune idée sur le positionnement des points. Dans un tel cas, vous devez aider en utilisant \dotsc pour les points suivis de virgules, \dotsb pour les points suivis de Opérateur binaire ou Symbole de relation, \dotsm pour les points suivis de points de multiplication, \dotsi pour les points suivis d’intégrales, ou \dotso dans tout autre cas.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3A series $H_1, H_2, \dotsc\,$, a sum
4$H_1 + H_2 + \dotsb\,$, an orthogonal product
5$H_1 \times H_2 \times \dotsm\,$, and an infinite
6integral: \[ \int_{H_1} \int_{H_2} \dotsi \;
7{-\Gamma}\, d\Theta \]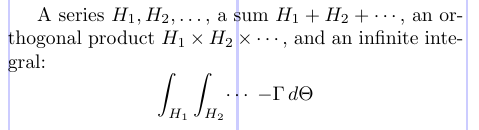

$Points de suspension à la fin d’une formule$

5.2. Symboles extensibles horizontalement

Fondamentalement, LaTeX permet de configurer n’importe quelle commande d’accent mathématique pour produire le glyphe approprié à partir d’une plage de largeurs lorsque celles-ci sont fournies par les polices disponibles. Cependant, dans LaTeX standard, il n’existe que deux commandes de ce type : \widehat et \widetilde.

Dans l’exemple suivant, nous démontrons l’utilisation de quelques commandes qui produisent des constructions similaires aux accents extensibles susmentionnés. Ils produisent tous des symboles composés du cours de mathématiques Ordinaire.

 1\usepackage{amsmath}
 2% -------------------------------------------------------------------------------
 3\begin{align*}
 4\widehat {\psi_\delta(t) E_t h}
 5&= \widetilde {\psi_\delta(t) E_t h} \\
 6\overline {\psi_\delta(t) E_t h}
 7&= \underline {\psi_\delta(t) E_t h} \\
 8\overbrace {\psi_\delta(t) E_t h}
 9&= \underbrace {\psi_\delta(t) E_t h}
10& & \text{Do not change style} \\
11\overrightarrow {\psi_\delta(t) E_t h} 
12&= \overleftarrow {\psi_\delta(t) E_t h}
13& & \text{Do not change style} \\[-3pt]
14& & & \text{without \textsf{amsmath}} \\
15\underrightarrow {\psi_\delta(t) E_t h}
16&= \underleftarrow {\psi_\delta(t) E_t h}
17& & \text{Do need \textsf{amsmath}} \\
18\overleftrightarrow {\psi_\delta(t) E_t h}
19&=\underleftrightarrow{\psi_\delta(t) E_t h}
20& & \text{Do need \textsf{amsmath}}
21\end{align*}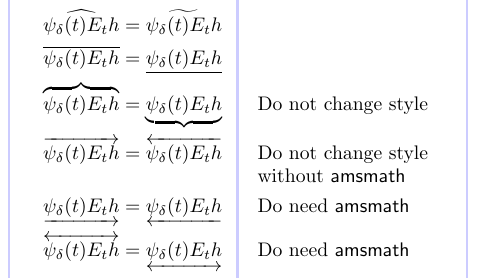

$Accents extensibles$

Ici, « changer de style » signifie que le symbole utilisé est affecté par le style mathématique utilisé afin qu’il ait un aspect correct lorsqu’il est utilisé, par exemple, en fractions ou en indice/exposant. Ceux qui ne changent pas de style n’apparaîtront qu’au niveau supérieur des formules affichées.

5.3. Symboles extensibles verticalement

L’extensibilité verticale est beaucoup plus large. Le tableau suivant répertorie tous les symboles extensibles verticalement.

Symboles extensibles verticalement


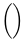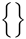$“Parenthèses”$	`(` `)`	$“Accoudoirs ouverts”$	`\{` `\}`	$“Doubles barres verticales”$	`\lVert` `\rVert`
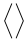$“Crochets angulaires”$	`\langle` `\rangle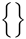`	$“Accoudoirs fermés”$	`\lbrace` `\rbrace`	$“Barres verticales simples”$	`\lvert` `\rvert`
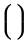$“Lgroup et Rgroup”$	`\lgroup` `\rgroup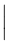`	$“Crochets ouverts”$	`[` `]`	$“Barre verticale”$	`
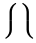$“Moustaches”$	`\lmoustache` `\rmoustache`	$“Crochets fermants”$	`\lbrack` `\rbrack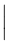`	$“Barre verticale”$	`\vert`
$“Flèche vers le bas”$	`\Downarrow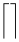`	$“Supports de plafond ouverts”$	`\lceil` `\rceil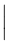`	$“Barre de flèche verticale”$	`\arrowvert`
$“Flèche vers le haut”$	`\Uparrow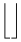`	$“Fermeture des crochets de plancher”$	`\lfloor` `\rfloor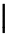`	$“Barre verticale d’accolade”$	`\bracevert`
$“Flèche haut bas”$	`\Updownarrow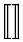`	$“Doubles crochets ouverts”$	`\llbracket` `\rrbracket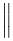`	$“Double barre verticale”$	`\Arrowvert`
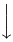$“Flèche simple vers le bas”$	`\downarrow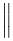`	$“Barre oblique”$	`/`	$“Double ligne verticale”$	`\|`
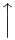$“Flèche simple vers le haut”$	`\uparrow`	$“Barre oblique inverse”$	`\backslash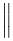`	$“Double ligne verticale”$	`\Vert`
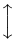$“Flèche simple vers le haut et vers le bas”$	`\updownarrow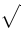`		`.`	$“Signe de racine carrée”$	`\sqrtsign`

Les symboles en italique nécessitent soit le package amsmath, soit, s’ils sont en plus saisis en gras, le package stmaryrd. Un point (.) n’est pas en soi un symbole extensible, mais il peut être utilisé pour produire un délimiteur « invisible ». Le symbole \sqrtsign ne peut pas être utilisé avec \left, \right ou \middle.

Synonymes : [ - \lbrack, [; ] - \rbrack, ]; { - \lbrace, \{; } - \rbrace, \}; | - \vert, |; || - \Vert, \|.

Ces symboles ne deviennent extensibles que dans certains usages. Ils doivent reposer sur la construction suivante :

1\left <ext-Open> <sub-formula> \right <ext-Close>

Si LaTeX utilise le programme eTeX, vous pouvez également utiliser ces symboles extensibles avec \middle.

Ici, <ext-Open> et <ext-Close> peuvent être n’importe lequel des symboles (sauf \sqrtsign) répertoriés dans le tableau ci-dessus. Il doit s’agir de symboles configurés pour être extensibles comme décrit dans le fntguide. Ainsi, un symbole représentant l’absence de glyphe réel doit être disponible. Il se trouve que ce symbole, également connu sous le nom de délimiteur nul, est le point (.). Les tailles des glyphes réels pour la composition d’un symbole extensible sont choisies pour s’adapter à la hauteur et à la profondeur de la sous-formule qui se situe entre eux.

Le symbole radical \sqrtsign s’agrandit à la fois verticalement et horizontalement pour s’adapter à la taille de son argument. Dans LaTeX, vous préférez utiliser la commande \sqrt pour obtenir ce symbole.

1\[
2  \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 +
3    \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 + x}}}}}}
4\]

$Radicaux étendus$

Symboles décorés et structures composées Texte dans les formules mathématiques