9. Symboles dans les formules mathématiques | Manuel LaTeX

Les tableaux de cet article répertorient la large gamme de symboles mathématiques fournis par les packages AMS-LATEX, y compris les commandes pour accéder à chaque symbole. Ils incluent également les symboles supplémentaires de la police St Mary Road conçue par Allan Jeffrey et Jeremy Gibbons. Ce package étend les collections de polices de symboles Computer Modern et AMS et doit normalement être chargé en plus de « amssymb », mais toujours après celui-ci. Il fournit des symboles supplémentaires pour des domaines tels que la programmation fonctionnelle, l’algèbre des processus, la théorie des domaines, la logique linéaire et bien d’autres.

Les tableaux indiquent quels packages supplémentaires doivent être chargés pour utiliser chaque commande symbol. Les symboles avec les noms de commandes en noir sont disponibles dans LaTeX standard. Les symboles avec des noms de commande en bleu nécessitent le chargement de « amsmath », « amssymb » ou « stmaryrd ». Si nécessaire, une classification plus approfondie est donnée par des marquages : ^(StM) signifie un symbole de stmaryrd lorsque le tableau contient également des symboles d’autres packages ; ^(kernel) marque les symboles disponibles dans LaTeX standard mais uniquement en combinant deux ou plusieurs glyphes, alors qu’un seul glyphe existe dans le package indiqué ; et ^(var) marque les “Symboles alphabétiques” (de type \mathalpha) qui changent d’apparence lorsqu’ils sont utilisés dans le cadre d’un identifiant d’alphabet mathématique.

9.1. Cours de symboles mathématiques

La classification principale des symboles mathématiques est liée à leur signification dans l’usage technique. En typographie mathématique, cette classification définit la disposition des formules. En particulier, le formateur mathématique de TeX ajuste l’espace horizontal de chaque côté de chaque symbole en fonction de sa classe mathématique. Cette classification fait également des distinctions plus fines, par exemple entre les accents et les symboles simples et en divisant l’énorme liste de symboles Relation en plusieurs tableaux.

La configuration mathématique place chaque symbole dans l’une de ces classes : Ordinaire (Ord), Opérateur (Op), Binaire (Bin), Relation (Rel), Ouverture (Ouvert), Closing (Fermer) ou Punctuation (Punct). La classe du symbole peut être explicitement modifiée en utilisant les commandes \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathopen et \mathpunct. Dans l’exemple suivant, \# et \top (tous deux Ord par défaut) sont transformés en Rel et Op.

1\usepackage[fleqn]{amsmath}
2\[ a \# \top _x^\alpha x^\alpha_b \]
3\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]

$Changement explicite de la classe de symboles$

En plus des classes ci-dessus, certaines sous-formules - principalement les fractions et celles produites par \left et \right - forment une classe appelée Inner, qui est explicitement disponible via la commande \mathinner.

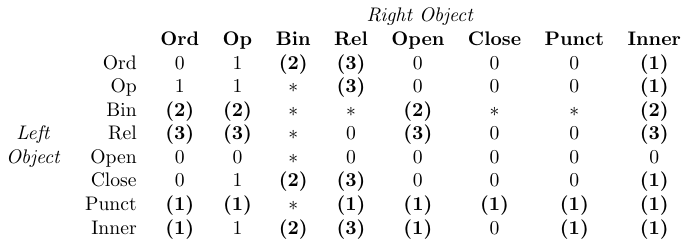
$Classes de symboles et espacement$

Dans le tableau, “0” signifie “pas d’espace”, “1” signifie \ Thinmuspace, “2” signifie \medmuskip, “3” signifie \thickmuskip, “*” signifie “impossible”. Les entrées en gras signifient que l’espacement correspondant n’est pas ajouté dans les styles d’écriture mathématique.

TeX gère l’espacement dans les formules simplement en identifiant la classe de chaque objet dans une formule, puis en ajoutant un espace entre chaque paire d’objets adjacents comme défini par le tableau précédent. Ce tableau est codé en dur dans les routines de composition mathématique de TeX et ne peut donc pas être modifié par les packages de macros.

Un symbole Binaire est transformé en symbole Ordinaire dès lors qu’il n’est pas précédé et suivi de symboles de nature compatible avec une opération binaire. C’est pourquoi certaines entrées du tableau sont marquées comme impossibles. Par exemple, $+x$ donne +x (un plus unaire) et non + x. Ce dernier peut être produit par ${}+x$ .

Considérez la formule suivante (les valeurs par défaut sont modifiées pour afficher plus clairement les espaces ajoutés) :

1thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[
4a - b = -\max \{ x , y \}
5\]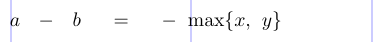

$\thinmuskip, \medmuskip et \thickmuskip$

TeX identifie les objets comme Ord, Bin, Ord, etc., puis insère des espaces comme suit :

1 A      -      b      =      -    \max   \{   x    ,       y   \}
2Ord \: Bin \: Ord \; Rel \; Ord \, Op   Open Ord Punct \, Ord Close

Le moins devant \max est transformé en Ordinaire car un Binaire ne peut pas suivre une Relation.

Dans une construction “\left...\right”, la sous-formule entière délimitée par la construction devient un objet unique de classe Inner. En revanche, les commandes comme \Bigl et \Bigr produisent respectivement des symboles individuels des classes Opening et Closing. La différence entre eux est révélée dans le tableau d’espacement ci-dessus. Bien qu’ils puissent donner lieu à des délimiteurs de taille verticale égale, des différences d’espacement peuvent survenir en fonction des objets adjacents dans la formule. Par exemple, Ordinary suivi de Opening n’obtient aucun espace, tandis que Ordinary suivi de Inner est séparé par un espace fin. Les espaces à l’intérieur de la sous-formule dans une construction “\left...\right” sont créés comme prévu, commençant par un symbole Opening et se terminant par un symbole Closing.

1\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]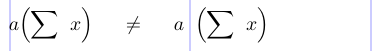

$\left…\right et \Bigl…\Bigr$

En résumé, mieux vaut vérifier qu’un symbole appartient à la classe souhaitée, plutôt que de simplement le rechercher dans les tableaux qui suivent.

9.2. Lettres, chiffres et autres symboles ordinaires

Les lettres latines ASCII non accentuées et les chiffres arabes sont tous appelés « symboles alphabétiques ». La police dans laquelle ils sont saisis peut varier. Dans les formules mathématiques, la police par défaut pour les lettres latines est italique, tandis que pour les chiffres arabes, elle est droite/romaine. Les symboles alphabétiques sont tous de classe Ordinaire.

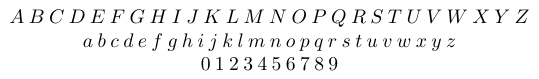
$Symboles de la classe \mathord (grec)$

Contrairement aux lettres latines, les lettres mathématiques grecques ne sont plus étroitement liées aux glyphes utilisés pour composer le texte grec normal. En raison d’un curieux hasard du XVIIIe siècle, dans la grande tradition européenne de la typographie mathématique, la police par défaut des lettres grecques minuscules dans les formules mathématiques est italique, tandis que pour les lettres grecques majuscules, elle est droite/romaine. (En physique et en chimie, par exemple, les traditions typographiques sont légèrement différentes.)

Les lettres grecques majuscules dans les premières lignes du tableau suivant sont également des symboles alphabétiques dont la police varie, la valeur par défaut étant verticale/romaine. Il existe des lettres majuscules grecques, dont chacune a la même apparence qu’une lettre latine (par exemple, A et Alpha, B et Beta, K et Kappa, O et *Omicron. *). Ces lettres ne sont pas présentes dans le tableau. Pour la même raison, il n’y a pas d’omicron minuscule. En pratique, les lettres grecques qui ressemblent aux lettres latines ne sont pas utilisées dans les formules mathématiques.

$Lettres grecques$

Les symboles en bleu nécessitent le package amssymb. ^(var) indique un symbole alphabétique variable.

Le tableau suivant répertorie d’autres symboles en forme de lettre de la classe Ordinaire. Les quatre premiers sont des lettres hébraïques.

$Symboles de la classe \mathord (en forme de lettre)$

Les symboles en bleu nécessitent le package amssymb.

Le tableau suivant répertorie les symboles restants de la classe Ordinaire, y compris certains signes de ponctuation courants. Ceux-ci se comportent comme des lettres et des chiffres, de sorte qu’il n’y a jamais d’espace supplémentaire autour d’eux.

$Symboles de la classe \mathord (divers)$

Les symboles en bleu nécessitent soit le package amssymb, soit, s’ils sont signalés par ^(StM), le package stmaryrd.

Notez que le signe d’exclamation, le point et le point d’interrogation ne sont pas traités comme des signes de ponctuation dans les formules.

Synonymes : négation logique - \lnot, \neg ; | - \vert, | ; || - \Vert, \|.

Une erreur courante consiste à utiliser ces symboles directement comme opérateurs binaires ou symboles Relation, sans utiliser une commande de symbole mathématique correctement définie pour ce type. Ainsi, si vous utilisez des commandes telles que \#, \square ou \&, vérifiez soigneusement que vous obtenez les bons espaces inter-symboles ou, mieux encore, définissez votre propre commande de symbole.

1\usepackage[fleqn]{amsmath} \usepackage{amssymb}
2\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
3\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
4% -------------------------------------------------------------------------------
5\[ a \neg b \qquad x \square y + z \]
6\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
7\[ a \bneg b \qquad x \rsquare y + z \]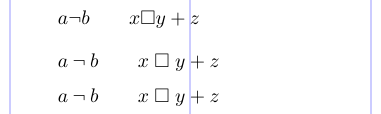

$Déclarer des symboles mathématiques$

La commande \DeclareMathSymbol est utilisée pour déclarer votre propre nom de symbole.

1\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}

Le premier argument est le nom de la commande que vous avez choisie. Le deuxième argument est l’une des commandes correspondant à la classe de symboles. Le troisième argument identifie la police de symbole à partir de laquelle le symbole doit être récupéré. Le quatrième argument donne la position du symbole dans l’encodage de la police, soit une valeur décimale, octale ou hexadécimale. Les valeurs correctes pour les arguments peuvent être trouvées plus facilement en consultant les définitions dans le fichier « amssymb.sty » ou « fontmath.ltx » (pour les symboles principaux). Par exemple, nous avons recherché \neq et \square, remplacé le \mathord dans chaque cas et finalement donné un nouveau nom au symbole résultant.

9.3. Accents mathématiques

Le tableau ci-dessous répertorie les commandes d’accent disponibles dans les formules. La plupart d’entre eux sont définis dans le standard TeX. Voir ici pour plus d’informations sur les accents extensibles. Lorsque vous ajoutez un accent mathématique à un symbole, le résultat est un symbole de classe Ordinaire.

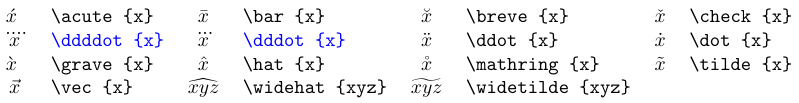
$Accents mathématiques, donnant des sous-formules de classe \mathord$

Les accents en bleu nécessitent le package amsmath.

Les deux derniers accents sont disponibles dans une gamme de largeurs, la plus grande étant automatiquement utilisée.

1\usepackage{amstext}
2% -------------------------------------------------------------------------------
3\[ a = b \text{ but } a \tilde{=} b
4\text{ which is not } a \mathrel{\tilde{=}} b \]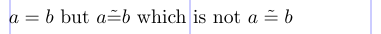

$Créer un symbole de relation à partir d’un symbole accentué$

D’autres façons de placer des symboles sur les symboles Relation sont présentées ici. Lorsque vous ajoutez un accent à un i ou un j dans des formules mathématiques, il est préférable d’utiliser les variantes sans point \imath et \jmath.

9.4. Symboles d’opérateur binaire

Il existe plus de 100 symboles de classe Binaire parmi lesquels choisir. La plupart d’entre eux sont répertoriés dans le tableau suivant. Certains d’entre eux sont également disponibles sous forme de symboles Relation, bien que sous des noms différents.

$Symboles de la classe \mathbin (divers)$

Les symboles en bleu nécessitent soit le package amssymb, soit, s’ils sont signalés par ^(StM), le package stmaryrd.

Les triangles gauche et droit sont également disponibles sous forme de symboles Relation.

Le package stmaryrd transforme de manière déroutante les symboles Binaires \bigtriangleup et \bigtriangledown en Opérateurs, ne laissant que les synonymes \varbigtriangleup et \varbigtriangledown pour les formes d’opérateurs Binaires.

Le package amssymb propose quelques symboles de boîte à utiliser comme opérateurs binaires ; beaucoup d’autres sont ajoutés par stmaryrd. Voir le tableau suivant.

$Symboles de la classe \mathbin (boxes)$

Tous les symboles nécessitent soit le package amssymb ou, s’ils sont signalés par ^(StM), le package stmaryrd.

Vous pouvez charger le package stmaryrd avec l’option heavycircles. En conséquence, chaque commande de symbole de cercle du tableau suivant qui commence par \var échange sa définition avec la commande correspondante sans le “var” ; par exemple, le symbole \varodot devient \odot, et vice versa.

$Symboles de la classe \mathbin (cercles)$

Les symboles en bleu nécessitent soit le paquet amssymb, soit, s’ils sont signalés par ^(StM), le paquet stmaryrd.

L’option heavycircles du paquet stmaryrd affecte toutes les commandes commençant par \var et leurs variantes normales.

9.5. Symboles de relation

La classe des symboles binaires Relation est encore plus grande que celle des opérateurs Binary. Le tableau suivant répertorie les symboles d’égalité et d’ordre. Une barre oblique peut être insérée dans n’importe quel symbole Relation en la faisant précéder de la commande \not. Le symbole nié représente le complément (ou la négation) des relations.

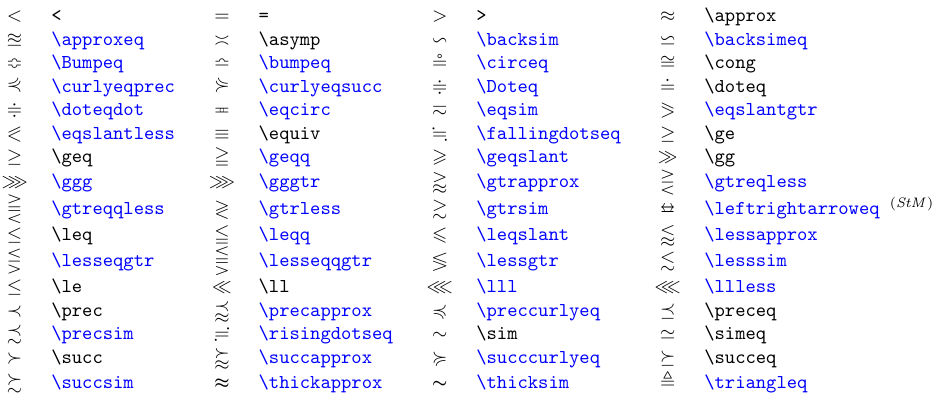
$Symboles de la classe \mathrel (égalité et ordre)$

Les symboles en bleu nécessitent soit le paquet amssymb ou, s’il est signalé ^(StM), le paquet stmaryrd.

1$ u \not< v$ or $a \not\in \mathbf{A} $

$Nier une relation$

Cette méthode générique de négation d’un symbole Relation ne donne pas toujours de bons résultats, surtout avec des symboles plus grands, car la barre oblique aura toujours la même taille, la même position et la même pente. De ce fait, certains « symboles niés » spécialement conçus sont également disponibles. Voir la liste dans le tableau suivant.

$Symboles de classe \mathrel (égalité et ordre�négués)$

Les symboles en bleu nécessitent le package amssymb.

Si un choix est disponible, il est généralement préférable d’utiliser les glyphes spécialement conçus. Pour comprendre pourquoi, comparez les symboles de l’exemple suivant.

1\usepackage{amssymb}
2% -------------------------------------------------------------------------------
3$ \not\leq \ \not\succeq \ \not\sim $ \par
4$ \nleq \ \nsucceq \ \nsim $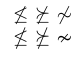

$Symboles de relation niés composés et spécialement conçus$

Le tableau suivant répertorie les symboles Relation pour les ensembles et les inclusions.

$Symboles de la classe \mathrel (ensembles et inclusion)$

Les symboles en bleu nécessitent soit le paquet amssymb ou, s’ils sont signalés par ^(StM), le paquet stmaryrd.

Et maintenant les négations des symboles Relation pour les ensembles et l’inclusion.

$Symboles de la classe \mathrel (ensembles et inclusion-négation)$

Les symboles en bleu nécessitent le package amssymb.

Le tableau suivant répertorie les symboles Relation en forme de flèche. Certaines constructions de flèches extensibles qui produisent des symboles composés Relation sont décrites ici.

$Symboles de la classe \mathrel (flèches)$

Les symboles en bleu nécessitent soit le paquet amssymb ou, s’ils sont signalés par ^(StM), le paquet stmaryrd.

Et voici les symboles Relation en forme de flèche niés.

$Symboles de la classe \mathrel (flèches-négées)$

Les symboles en bleu nécessitent le package amssymb.

Il existe d’autres éléments (en plus de \not utilisé pour annuler les symboles généraux Relation) qui ont été spécialement conçus pour annuler ou étendre les symboles en forme de flèche. Voir le tableau suivant.

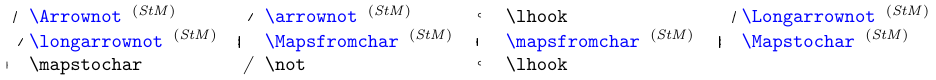
$Symboles de la classe \mathrel (négation et extensions de flèches))$

Les symboles en bleu nécessitent le package stmaryrd.

Ces symboles sont destinés à être combinés, principalement avec des flèches ; par exemple, \longarrownot\longleftarrow.

Utilisez \joinrel pour « coller » des symboles relationnels ensemble, par exemple, \lhook\joinrel\longrightarrow.

Les dimensions de ces symboles les rendent inadaptés à d’autres utilisations.

1\usepackage{stmaryrd}
2% -------------------------------------------------------------------------------
3$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$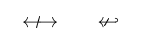

$Flèche négations$

Enfin, vous trouverez ci-dessous d’autres symboles Relation divers.

$Symboles de la classe \mathrel (divers)))$

Les symboles Relation en bleu nécessitent le package amssymb.

\therefore est un symbole Relation, son espacement peut donc ne pas être celui attendu dans les utilisations courantes.

Polices dans les formules mathématiques Symboles mathématiques LaTeX et leurs compagnons