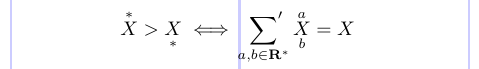4. Simboli decorati e strutture composte

Il pacchetto amsmath fornisce alcuni comandi per produrre strutture come oggetti simili alla frazione e simboli decorati. Questo discute su alcuni di loro.

4.1. Frazioni generali

Il pacchetto amsmath definisce il comando \genfrac, che produce una frazione generalizzata.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

I primi due argomenti definiscono rispettivamente delimitatori sinistro e destro. Usando il terzo argomento, spesso, è possibile sovrascrivere lo spessore predefinito della regola della frazione. Ad esempio, i coefficienti binominali (vedi sotto) usano il valore 0pt per questo argomento per rendere invisibile la linea. Il valore predefinito (quando lasciato vuoto) dello spessore della linea è determinato dalla configurazione del carattere corrente per la composizione matematica. Il seguente elenco contiene impostazioni predefinite utilizzate negli esempi di questo articolo.

Style	Default Thickness
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

Il quarto argomento, *stile *, sostituisce (se non lasciato vuoto) lo stile matematico per il layout e le dimensioni del carattere utilizzate. Il valore deve essere nell’intervallo 0-3: 0 - \displaystyle, 1 -\textstyle, 2 - \scriptstyle, 3 -\scriptscriptstyle. Se questo argomento viene lasciato vuoto, lo stile viene selezionato in base alle normali regole per le frazioni. Gli ultimi due argomenti sono il numeratore e il denominatore.

I vecchi comandi di frazione \over, \overwithdelims, \atop, \atopwithdelims, \above e \abovewithdelims, che il LaTeX standard eredita da TeX, generano avvisi quando vengono utilizzati con il pacchetto amsmath.

4.1.1. Frazioni semplici

Avendo il comando \genfrac, il pacchetto amsmath definisce anche tre comandi come comode stendi: \frac,\dfrac e \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

L’esempio seguente dimostra l’uso di questi comandi:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.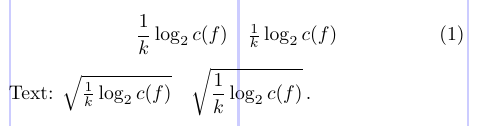

4.1.2. Coefficienti binomiali

Un’altra struttura a forma di frazione sono i coefficienti binomiali. Per aiutarti a comprometterli, il pacchetto amsmath fornisce comandi simili \binom, \dbinom e \tbinom.

Ecco come abbreviano il comando \genfrac:

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

Ed ecco l’esempio:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.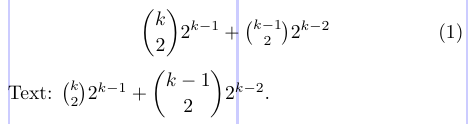

4.1.3. Frazioni continue

Se è necessario compromettere un array di frazione, che è essenzialmente una frazione infinita, nota anche come “frazione continua”, c’è il comando \cFrac nel pacchetto amsmath. Passa l’argomento opzionale [l] o [r] per allineare un numeratore a sinistra o a destra, che è centrato per impostazione predefinita.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}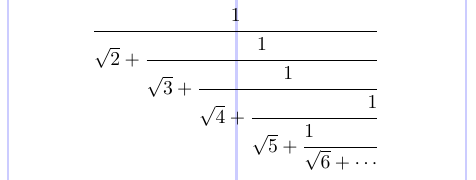

4.2. Matematica in scatola

Il pacchetto amsmath fornisce il comando \boxed simile a \fbox per mettere il contenuto della modalità matematica in una scatola.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}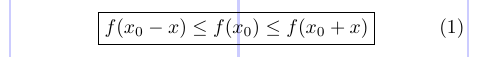

4.3. Posizionando i limiti

Abbonamenti e apice su integrali, somme, prodotti o altri operatori possono essere posizionati sopra e sotto l’operatore di matematica (la “posizione limite”) o nella posizione del pedice/apice sulla destra dell’operatore. In genere, i limiti non vengono utilizzati nel testo (altrimenti le righe possono diffondersi). In una formula visualizzata, il posizionamento dipende dall’operatore. L’esempio seguente mostra il posizionamento predefinito in LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.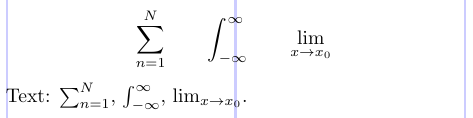

Il pacchetto amsmath ‘offre opzioni per il controllo del posizionamento. Sono elencati di seguito, dove predefinito segna il comportamento nel caso in cui il pacchetto amsmath ‘sia utilizzato con una classe di documenti in LaTeX standard ma senza nessuna di queste opzioni.

intlimits, nointlimits	Posiziona gli apici/pedici dei simboli di integrazione rispettivamente sopra e sotto o lateralmente (impostazione predefinita). Utilizzato solo nelle formule visualizzate.
sumlimits, nosumlimits	Posiziona gli apici/pedici degli operatori di grandi dimensioni (somma, prodotto, ecc.) rispettivamente sopra e sotto (impostazione predefinita) o lateralmente. Utilizzato solo nelle formule visualizzate.
namelimits, nonamelimits	Simile a sumlimits o nosumlimits, ma per alcuni operatori, o “nomi di operatore”, come inf, sup, lim, min, max, che tradizionalmente sono composti con pedici sottostanti, almeno quando compaiono in una formula visualizzata.

Tex ha tre comandi primitivi che, sono apparsi immediatamente dopo il simbolo o il nome dell’operatore, controllano il posizionamento di abbonamenti/apice: \limiti,\nolimits e \Displaylimits. Il comando \Displaylimits ‘produce abbonamenti/apice in posizione limite quando l’attuale stile matematico è uno stile di visualizzazione. Questo è il comportamento predefinito ogni volta che appare un simbolo dell’operatore di classe * o viene utilizzato un comando \mathop. Se è necessario compromettere un operatore con abbonamenti/apice in posizione limite al di fuori di un display, è necessario dichiararlo individualmente utilizzando il comando \Limits.

Confronta il seguente esempio con quello precedente.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.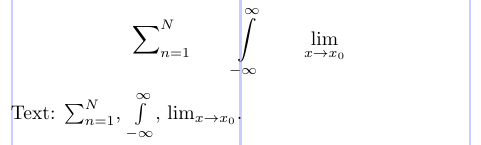

4.3. Integrali multipli

Per scrivere più segni integrali con spazi ben adattati tra loro sia nel testo che nei display, utilizzare i comandi \iint,\iiint e \iiiint. \IDotsint produce due segni integrali con punti Ellipsis tra loro.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}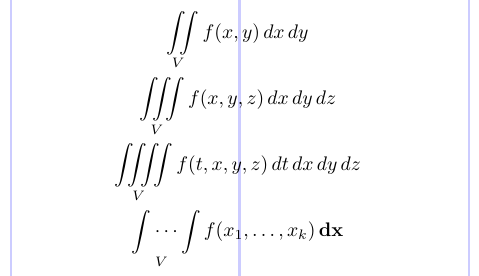

4.4. Relazioni modulari

La notazione “mod” per le classi di equivalenza di numeri interi è governata dalle convenzioni di spaziatura speciali. Per affrontarlo, il pacchetto amsmath offre comandi \mod, \bmod,\pmod e \pod. Il seguente esempio mostra l’uso di questi comandi.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}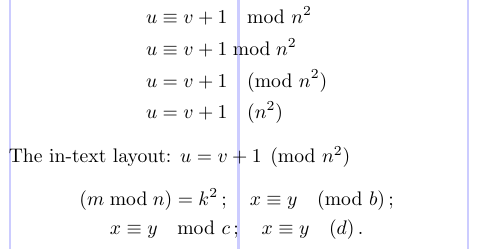

Con amsmath, la spaziatura di \pmod viene ridotta all’interno di una formula non visualizzata.

4.5. Accenti matematici a punti

Oltre agli accenti matematici \dot e \ddot, il pacchetto amsmath fornisce i comandi \dddot e \ddddot, che producono rispettivamente accenti a dot tripli e quadrupli.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Creazione di aprile dagli accenti: il pacchetto amsxtra

Il pacchetto Amsxtra offre una funzione utile, una raccolta di semplici comandi per posizionare accenti come apripisti per la subformance:

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$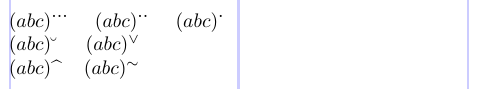

4.7. Altre decorazioni

Il LaTeX standard ha il comando \stackrel che pone un apice sopra un simbolo relazione. Inoltre, il pacchetto amsmath definisce i comandi\overset e \underserset. Usalo per posizionare il materiale sopra o sotto qualsiasi simbolo Ordinary o Relation* o Operatore binario.

Il comando \sideet aggiunge decorazioni a qualsiasi simbolo operatore (somma, prodotto, ecc.) Oltre ai limiti normali. Questi sono inseriti nelle posizioni del pedice e appescript a sinistra e a destra dell’operatore *.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]