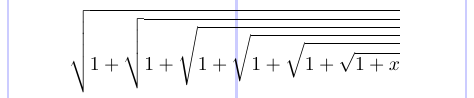5. Simboli estensibili e regolabili

Nel LaTeX, ci sono alcune caratteristiche che consentono di produrre strutture che possono crescere fino a qualsiasi dimensione richiesta. La composizione matematica ha un disperato bisogno di tale variabilità. Ne discuteremo alcuni aspetti in questo articolo. Tutti i comandi trattati in questa sezione (se non diversamente indicato) sono forniti dal LaTeX standard.

5.1. Ellipsis …

Il pacchetto amsmath sostituisce (in quasi tutti i casi) tutti quei\ldots, CDOTS, ecc. Dal LaTeX standard con il comando singolo\dots. Sia la posizione verticale dell’ellissi che lo spazio intorno a essa vengono automaticamente selezionati a seconda del tipo di simbolo che segue \dots. Se il simbolo successivo è, diciamo, un segno più, i punti usciranno centrati; Se si tratta di una virgola, cadranno sulla linea di base. Sono sempre tre punti ma la spaziatura è variabile.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
A series $H_1, H_2, \dots, H_n$, a sum
$H_1 + H_2 + \dots + H_n$, an orthogonal product
$H_1 \times H_2 \times \dots \times H_n$.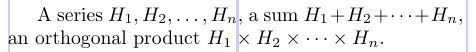

Tuttavia, quando i punti appaiono alla fine di una formula, l’oggetto successivo sarà qualcosa di simile a \end o\)o$, e non dà il LaTeX a non indizio sul posizionamento dei punti. In tal caso, è necessario aiutare usando \dotsc per punti seguiti da virgole,\dotsb per punti seguiti da operatore binario o *simbolo di relazione *, \dotsm per punti seguiti da punti di moltiplicazione,\dotsi per punti seguiti da integrali o \dotso in qualsiasi altro caso.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
A series $H_1, H_2, \dotsc\,$, a sum
$H_1 + H_2 + \dotsb\,$, an orthogonal product
$H_1 \times H_2 \times \dotsm\,$, and an infinite
integral: \[ \int_{H_1} \int_{H_2} \dotsi \;
{-\Gamma}\, d\Theta \]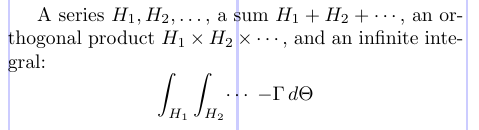

5.2. Simboli che sono orizzontalmente estensibili

Fondamentalmente, il LaTeX consente di impostare qualsiasi comando accento matematico per produrre il glifo appropriato da una serie di larghezze ogni volta che questi sono forniti dai caratteri disponibili. Tuttavia, nel LaTeX standard ci sono solo due di questi comandi: \widehat e \widetilde.

Nel prossimo esempio, dimostriamo l’uso di alcuni comandi che producono costrutti simili agli accenti estensibili di cui sopra. Tutti producono simboli composti della classe matematica *ordinaria *.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
\widehat {\psi_\delta(t) E_t h}
&= \widetilde {\psi_\delta(t) E_t h} \\
\overline {\psi_\delta(t) E_t h}
&= \underline {\psi_\delta(t) E_t h} \\
\overbrace {\psi_\delta(t) E_t h}
&= \underbrace {\psi_\delta(t) E_t h}
& & \text{Do not change style} \\
\overrightarrow {\psi_\delta(t) E_t h} 
&= \overleftarrow {\psi_\delta(t) E_t h}
& & \text{Do not change style} \\[-3pt]
& & & \text{without \textsf{amsmath}} \\
\underrightarrow {\psi_\delta(t) E_t h}
&= \underleftarrow {\psi_\delta(t) E_t h}
& & \text{Do need \textsf{amsmath}} \\
\overleftrightarrow {\psi_\delta(t) E_t h}
&=\underleftrightarrow{\psi_\delta(t) E_t h}
& & \text{Do need \textsf{amsmath}}
\end{align*}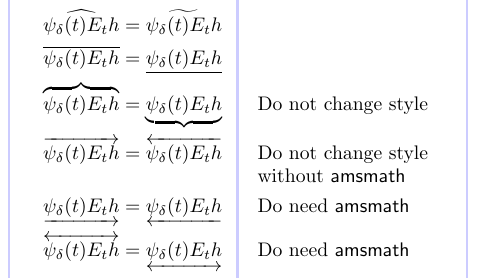

Qui, “stile di cambiamento” significa che il simbolo impiegato è influenzato dallo stile matematico in uso in modo che sembri giusto quando usato, ad esempio, in frazioni o pedice/apice. Quelli che non cambiano lo stile usciranno proprio al livello più alto delle formule visualizzate.

5.3. Simboli che sono verticalmente estensibili

L’estensibilità verticale è molto più ampia. La tabella seguente elenca tutti i simboli che sono verticalmente estensibili.

Simboli verticalmente estensibili

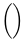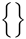	( )		\{ \}		\lVert \rVert
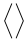	\langle \rangle		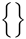\lbrace \rbrace		\lvert \rvert
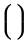	\lgroup \rgroup		[ ]		`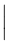
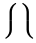	\lmoustache \rmoustache		\lbrack \rbrack		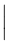\vert
	\Downarrow		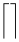\lceil \rceil		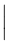\arrowvert
	\Uparrow		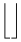\lfloor \rfloor		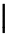\bracevert
	\Updownarrow		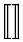\llbracket \rrbracket		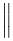\Arrowvert
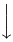	\downarrow		/		|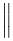
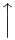	\uparrow		\backslash		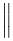\Vert
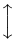	\updownarrow		.		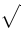\sqrtsign

I simboli in corsivo richiedono il pacchetto amsmath o, se ulteriormente scritti in grassetto, il pacchetto stmaryrd. Un punto (.) non è di per sé un simbolo estensibile, ma può essere utilizzato per creare un delimitatore “invisibile”. Il simbolo \sqrtsign non può essere utilizzato con \left, \right o \middle.

Synonyms: [ - \lbrack, [; ] - \rbrack, ]; { - \lbrace, \{; } - \rbrace, \}; | - \vert, |; || - \Vert, \|.

Questi simboli diventano estensibili solo in determinati usi. Devono essere basati sulla seguente costruzione:

\left <ext-Open> <sub-formula> \right <ext-Close>

Se LaTeX utilizza il programma eTeX, è possibile utilizzare questi simboli estensibili anche con \middle.

Qui <Ext-Open> e <Ext-Close> può essere uno qualsiasi dei simboli (tranne \sqrtsign) elencati nella tabella sopra. Devono essere simboli che sono stati impostati per essere estensibili come descritto nella FntGuide. Pertanto, deve essere disponibile un simbolo che rappresenta l’assenza di un vero glifo. È successo che questo simbolo, noto anche come Null Delimiter, è il periodo (.). Le dimensioni dei glifi effettivi per la composizione di un simbolo estensibile sono scelte per adattarsi all’altezza e alla profondità della sottospettazione che si trova tra di loro.

Il simbolo radicale \sqrtsign cresce sia verticalmente che orizzontalmente per adattarsi alle dimensioni della sua argomentazione. In LaTex, preferiresti usare il comando \sqrt per ottenere questo simbolo.

\[
  \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 +
    \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 + x}}}}}}
\]