8. Formule matematiche di perfezionamento

Abbiamo già discusso la maggior parte delle strutture necessarie per costruire formule di matematica. Ma ci sono ancora alcuni ottimi punti che ti permetteranno di produrre formule davvero belle, le formule che miglioreranno l’aspetto generale e la leggibilità dei libri e dei documenti che digiti.

8.1. Punteggiatura

La regola generale è: quando una formula è seguita da un periodo, virgola, punto e virgola, colon, punto interrogativo, punto esclamativo, ecc., Metti la punteggiatura dopo il $, quando la formula è nel testo; ma metti la punteggiatura prima il $$ quando viene visualizzata la formula. Per esempio,

If $x<0$, we have shown that $$y=f(x).$$

Quindi, non dovresti mai digitare nulla di simile

for $x = a, b$, or $c$.

Dovrebbe essere

for $x = a$, $b$, $c$.

Nel primo caso, Tex cominterà $ x = a, b $ come una singola formula, mettendo così uno spazio sottile tra la virgola e il b. Questo spazio non sarà lo stesso dello spazio tra la virgola e c, poiché gli spazi tra le parole sono sempre più grandi degli spazi sottili. Tale spaziatura sembra cattiva, ma nel secondo caso la spaziatura starà bene.

È anche importante che Tex non romperà mai una linea di paragrafo nello spazio tra la virgola e il b perché le pause dopo le virgole nelle formule sono generalmente sbagliate come nell’equazione$ x = f (x, a) $. Pertanto, viene inibita la possibilità di rompere le linee in un paragrafo, il che porta a un aspetto peggiore del documento di composizione. In altre parole, se un marchio di punteggiatura appartiene linguisticamente alla frase piuttosto che alla formula, lascialo al di fuori delle $.

8.2. Lettere non itaiche

Le funzioni matematiche comuni come “registro” sono sempre impostate in tipo romano. Il modo migliore per includere tali oggetti in una formula è utilizzare i seguenti comandi:

Nei seguenti esempi vengono utilizzati alcuni di questi comandi:

Le ultime due formule visualizzate mostrano che alcuni dei comandi sono trattati da Tex come grandi operatori con limiti come il segno di somma. E il pedice su \max non è trattato come il pedice su\log. Gli abbonamenti e i pignoli diventeranno limiti quando sono allegati a \det,\gcd, \inf,\lim, \liminf,\limsup, \max,\min, \pr e \sup, in stile display.

Se hai bisogno di un tipo romano per una funzione o un operatore di frequente che non è elencato sopra, è possibile definire facilmente il proprio comando. Supponiamo di voler definire un operatore con limiti e chiamarlo \oper. Per fare ciò, è necessario includere la seguente definizione nel preambolo:

\def\oper{\mathop{\rm oper}}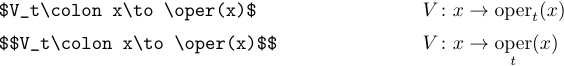

Nel caso in cui il tuo operatore non abbia limiti, usa una definizione come la seguente:

\def\oper{\mathop{\rm oper}\nolimits}

Se hai bisogno di un tipo romano solo per un singolo utilizzo, è più facile passare al tipo \rm come segue:

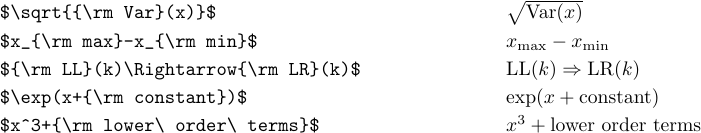
Notare gli usi di \ nell’ultimo caso. Senza di loro, gli spazi vuoti ordinari sarebbero stati ignorati e “termini di ordine inferiore” sarebbero stati composti come “LowerOrderTerms”.

La parola “mod”, che è generalmente ambientata anche in tipo romano in formule, ha bisogno di più cure, perché viene utilizzata in due modi diversi. Latex fornisce il comando \bmod da utilizzare quando" mod “è un’operazione binaria e il comando \pmod deve essere usato quando “mod” si verifica tra parentesi alla fine di una formula.

Si noti che \pmod inserisce le proprie parentesi; La quantità che appare dopo la “mod” in quella parentesi dovrebbe essere racchiusa in parentesi graffe a meno che non sia un singolo simbolo.

Puoi anche ottenere altri stili di tipo allo stesso modo in cui ottieni il tipo romano usando \rm. Ad esempio, \bf dà grassetto:

Puoi notare che ‘+’ e ‘=’ sono ancora di tipo romano. Il LaTeX imposta le cose in modo che comandi come \rm e \bf influenzino solo le lettere maiuscole a a z, le lettere minuscole a a z, le cifre 0 a 9, le lettere greche maiuscole \gamma to\omega e accenti matematiche come \tilde. Per inciso, in questo esempio non sono state usate pareti, poiché $ ‘hanno l’effetto del raggruppamento; \bf cambia il carattere corrente, ma il cambiamento è locale, quindi non influisce sul carattere che era corrente al di fuori della formula.

Puoi anche dire \cal nelle formule per ottenere lettere maiuscole in uno stile” calligrafico “.

This works only with the letters A to Z; you’ll get weird results if you apply \cal to lowercase or Greek letters.

C’è anche \mit, che sta per” matematico corsivo “. Ciò colpisce il greco maiuscolo.

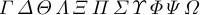
Quando \mit è in vigore, le lettere ordinarie a a z e a a z non sono cambiate; Sono ambientati in corsivo come al solito, perché di solito provengono dal carattere di matematica. Al contrario, lettere greche maiuscole e accenti matematici non sono influenzati da \rm, poiché normalmente provengono dal carattere romana.

Con LaTeX, puoi anche digitare \it o\tt per ottenere lettere di testo o da scrivere nel text nella tua formula. Probabilmente ti chiedi perché siano forniti sia \mit che\\. La risposta è che \mit è” matematica “(che di solito è il migliore per le formule), e\\ it è “text coitalic” (che di solito è meglio per eseguire il testo).

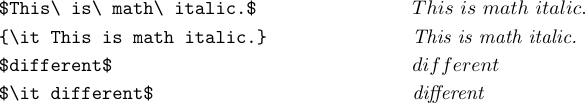
Le lettere di matematica sono più ampie e la spaziatura è diversa. Funziona meglio nella maggior parte delle formule, ma l’aspetto soffre quando si tenta di digitare alcune parole in corsivo come “diverse” in modalità matematica. Un ampio corsivo ‘f’ è generalmente desiderabile nelle formule, ma non nel testo. Pertanto, è meglio usare \\ in una formula che dovrebbe contenere una parola in corsivo reale. Questo di solito non è un caso di matematica classica, ma è un caso comune quando i programmi per computer vengono sottoposti a composizione:

Il secondo esempio mostra l’uso di brevi sottolinei per rompere i nomi degli identificatore.

8.3. Spaziatura tra formule

È un caso comune quando un display contiene più di una formula; Ad esempio, un’equazione può essere accompagnata da una condizione laterale:

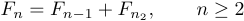
In tali casi è necessario dire a Tex quanto spazio mettere dopo la virgola, perché le normali convenzioni avrebbero raggruppato le cose insieme. Per ottenere questo, puoi digitare

$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.

Qui, \Qquad sta per” Double Quad “, dove” Quad “significa una quantità di spazio comune per le stampanti. Pertanto \quad significa il quad di uno spazio di una stampante nella direzione orizzontale. Ogni volta che si desidera spaziatura che differisce dalle convenzioni normali, è necessario specificarla esplicitamente usando comandi come \quad e \qquad.

Un quad era un pezzo quadrato di tipo vuoto, 1em largo e alto 1EM - approssimativamente le dimensioni di una capitale M; Ma il quad di LaTex non ha altezza.

Nel testo di un paragrafo, le formule sembrano migliori se sono separate da parole, non solo da virgole. Ma se non c’è davvero alcun testo da inserire, dovresti almeno mettere un po ‘di spazio tra le formule. Confrontare

The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.

E

The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.

che danno

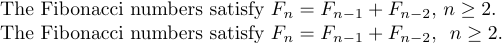
Il ‘' qui fornisce una separazione visiva che compensa in parte il cattivo stile.

8.4. Spaziatura all’interno di formule

Abbiamo già visto che Tex fa una spaziatura automatica di formule di matematica che le fa sembrare giusta nella maggior parte dei casi. Tuttavia, è naturale che sorgano eccezioni, poiché il numero di possibili formule è enorme e le regole di spaziatura di Tex siano abbastanza semplici. Quindi, è desiderabile avere unità di spaziatura raffinate per tali casi, invece dei grandi pezzi che derivano da \, \quad e \qquad.

Gli elementi di base dello spazio che Tex mette in formule sono chiamati *spazi sottili *, *spazi medi * e *spazi spessi *. Tex li inserisce automaticamente in formule, ma puoi aggiungere la tua spaziatura ogni volta che vuoi, usando i comandi

Le formule che coinvolgono il calcolo sembrano migliori quando viene inserito uno spazio extra sottile prima di * dx * o * dy * o d qualunque cosa; Ma Tex non lo fa automaticamente. I seguenti esempi mostrano come raccontare a Tex di queste esigenze:

Si noti che no \, era necessario dopo il ‘/’ nella seconda formula. Non è inoltre necessario \, nell’ultimo esempio, poiché il * dt * appare tutto da solo nel numeratore di una frazione; Questo lo stacca visivamente dal resto della formula.

Le unità fisiche, quando appaiono in una formula, dovrebbero essere impostate in tipo romano e separate dal materiale precedente da uno spazio sottile:

Gli spazi sottili devono anche essere inseriti dopo i punti esclamativi (operazione fattoriale), se il carattere successivo è una lettera o una cifra o un delimitatore di apertura:

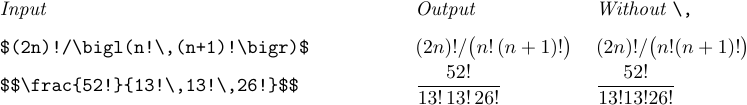
Oltre a questi casi, occasionalmente incontrerai formule in cui i simboli sono raggruppati troppo strettamente o dove appare troppo spazio bianco, a causa di alcune sfortunate combinazioni di forme. Un \, \! Applicato con gusto aprirà le cose o chiuderà le cose in modo che il lettore non sia distratto dal significato matematico della formula. I radicali e gli integrali multipli sono spesso candidati per una sintonizzazione così fine. Ecco alcuni esempi di situazioni da cercare:

Le regole di spaziatura di Tex a volte falliscono quando ‘|’ e ‘\ |’ apparire in una formula, perché questi simboli sono trattati come simboli ordinari anziché come delimitatori. Considera le formule

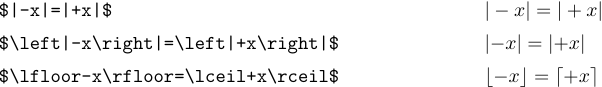
Nel primo caso la spaziatura è sbagliata perché Tex pensa che il segno più stia calcolando la somma di “|” e ‘x’. L’uso di \left e `\a destra “nel secondo esempio mette Tex sulla traccia destra. Il terzo esempio mostra che non sono necessarie tali correzioni con altri delimitatori, perché Tex sa se sono aperture o chiusure.

8.5. Ellissi

Un’ellissi può essere indicata da due diversi tipi di punti, uno superiore all’altro. Le migliori tradizioni distinguono tra queste due possibilità. È generalmente corretto produrre formule come

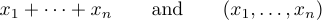
ma sbagliato a produrre formule come

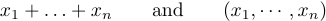
L’idea è di digitare \ldots quando si desidera tre punti bassi e\CDOTS quando si desidera tre punti centrati in verticale. In generale, è meglio usare \CDOTS tra segni+e - e moltiplicazione, e anche tra segni = o segni “meno di o uguali” o segni di sottoinsieme o altre relazioni simili. I punti bassi sono usati tra le virgole e quando le cose vengono giustapposte senza alcun segno tra loro:

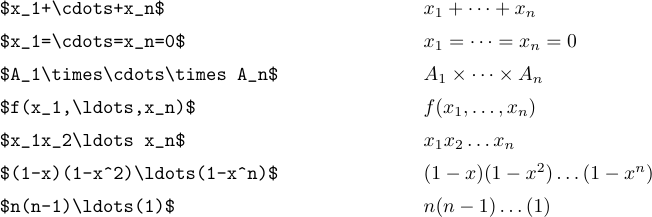
Ma c’è un caso speciale in cui \ldots e \CDOTS non producono la spaziatura giusta. Questo accade quando appaiono alla fine di una formula o poco prima di un delimitatore di chiusura. In tali situazioni è necessario uno spazio extra sottile. Ad esempio, considera le seguenti frasi:

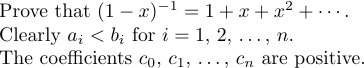
La prima frase viene prodotta dalla digitazione

Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.

Senza \, Il periodo sarebbe stato troppo vicino ai \CDOTS.

La seconda frase è stata digitata come:

Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.

Notare l’uso dei legami (~), che impediscono le cattive pause. Tali ellissi sono molto comuni in alcune forme di scrittura matematica, quindi il LaTeX fornisce la macro \dots come abbreviazione per$ \ ldots \, $da usare nel testo di un paragrafo. La terza frase può quindi essere digitata

The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.

8.6. Rottura della linea

Quando hai formule in un paragrafo, Tex potrebbe doverle spezzarle tra le linee. Romperà una formula solo dopo un simbolo di relazione, o dopo un simbolo di operazione binaria, in cui la relazione o l’operazione binaria sono al livello esterno della formula, il che significa non racchiuso in {...}. Ad esempio, se digiti

$f(x,y) = x^2-y^2 = (x+y)(x-y)$

Nel mezzo del paragrafo, esiste la possibilità che Tex si rompa dopo uno dei segni = (preferiti) o dopo il - o + o - (in caso di emergenza). Ma non ci sarà una pausa dopo la virgola in ogni caso, poiché le virgole dopo le quali sono auspicabili le pause non dovrebbero apparire tra $ ’s.

Non vuoi consentire la rottura in questo esempio tranne dopo i segni, potresti digitare

$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$

Perché queste parenti aggiuntive “congelano” le sottocamere, mettendole in scatole infrangibili. Ma non c’è bisogno di preoccuparsi di tali cose a meno che Tex non rompa effettivamente una formula, dal momento che la possibilità di questo è piuttosto bassa.

Se vuoi consentire la rottura ad un certo punto nel livello esterno di una formula, puoi dire `\consentire ‘. Ad esempio, se la formula

$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$

appare nel testo di un paragrafo, Tex permetterà che venga suddiviso in due pezzi

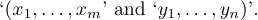
8.7. Bretelle

I simboli ‘{’ e ‘}’ sono usati in diverse notazioni e il LaTeX fornisce alcuni comandi per aiutarti a far fronte a formule che coinvolgono tali cose. Il caso più semplice è quando le parentesi graffe vengono utilizzate per indicare una serie di elementi. Ad esempio, “{a,b,c}” sta per l’insieme di tre elementia,b e c:

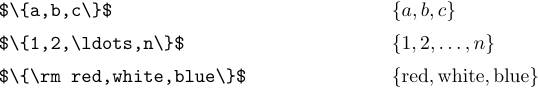
Un set può anche essere indicato dando un elemento generico seguito da una condizione specifica. Ad esempio, l’insieme di tutti gli oggetti x che è maggiore di 5 può essere scritto come segue:

Queste sono due varianti per indicare lo stesso set. Il primo richiede l’utilizzo di \mid per ottenere la barra verticale, mentre il secondo non richiede nulla tranne il colon, che viene trattato come un’operazione binaria.

Quando i delimitatori diventano più grandi, dovrebbero essere chiamati \bigl,\bigm e \bigr:

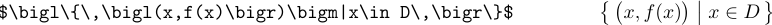
Le formule con delimitatori ancora più grandi userebbero comandi \big o\bigg o addirittura \bigg.

Potresti anche trovare un altro uso delle parentesi graffe nelle formule visualizzate. In realtà è un tutore sinistro che indica una scelta tra una serie di alternative:

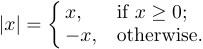
Questa costruzione può essere digitata usando il comando \case:

$$|x|=\case{x,&if $x\ge0$;\cr
            -x,&otherwise.\cr}$$

Ognuno dei casi ha due parti separate dal simbolo &, che svolge un ruolo speciale nella costruzione di strutture tabulari. A sinistra di & è una formula matematica che è implicitamente racchiusa in $ ... $; A destra di & è un testo ordinario. Quindi -x, nella seconda riga sarà composta in modalità matematica, ma il altrimenti sarà composto in modalità orizzontale. Gli spazi vuoti prima e dopo i & vengono ignorati. Ci possono essere un numero qualsiasi di casi, anche se di solito ce ne sono solo due. Ogni caso dovrebbe essere seguito da \cr.

Le parentesi graffe orizzontali verranno impostate sopra o sotto parti di una formula visualizzata se si utilizzano i comandi \overbrace o\underbrace. Tali cose sono considerate grandi operatori come \sum, quindi puoi mettere limiti al di sopra o al di sotto di loro specificando i supporti o gli abbonamenti:

8.8. Matrici

Le matrici sono oggetti abbastanza comuni nelle formule matematiche; Sono solo matrici rettangolari di formule disposti in file e colonne. Latex fornisce il comando \matrix per gestire i tipi più comuni di matrici.

Ad esempio, supponiamo di voler specificare il display

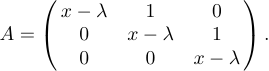
Tutto quello che fai è digitare

$$A=\left(\matrix{x-\lambda&1&0\cr
                  0&x-\lambda&1\cr
                  0&0&x-\lambda\cr}\right).$$

Questo è abbastanza simile alla costruzione \casi che abbiamo esaminato in precedenza; Ogni riga della matrice è follower da \cr e sono usati segni&tra le singole voci di ogni riga. Tuttavia, a differenza di \Cases, dovresti mettere i tuoi delimitatori\Left e \Right attorno alla matrice. Il motivo è che diversi delimitatori possono essere utilizzati in diverse costruzioni a matrice. D’altra parte, le parentesi vengono utilizzate più spesso di altri delimitatori, quindi puoi digitare \pMatrix se si desidera che il LaTeX imposti le parentesi per te:

$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$

Ogni voce di una matrice è normalmente centrata nella sua colonna e ogni colonna si espande quanto necessario per ospitare le voci che contiene e c’è un quad di spazio tra le colonne. Se vuoi qualcosa che esca a filo a sinistra/a destra nella sua colonna, seguilo/precederlo da \hfill.

Ogni voce di una matrice viene elaborata separatamente dalle altre ed è composta come una formula matematica in stile di testo. Pertanto, ad esempio, se dici \rm in una voce, non influisce sugli altri. Dire {\ rm x & y} non è valido.

Le matrici appaiono spesso come motivi generici che usano ellissi per indicare righe o colonne che vengono esclusi. È possibile scrivere tali matrici mettendo le ellissi nelle loro file e/o colonne. Oltre a \ldots, LaTex fornisce\vdots (punti verticali) e \ddots (punti diagonali) per tali costruzioni. Considera la seguente matrice

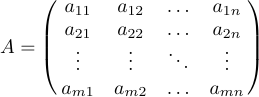
Questo è specificato come:

$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
             a_{21}&a_{22}&\ldots&a_{2n}\cr
             \vdots&\vdots&\ddots&\vdots\cr
             a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$

A volte una matrice è delimitata nella parte superiore e lasciata da formule che danno etichette alle righe e alle colonne. Per questa situazione, una macro speciale chiamata \bordermatrix è definita in LaTeX. Ad esempio, il display

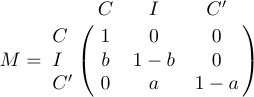
si ottiene quando si digita

$$M=\bordermatrix{&C&I&C'\cr
                C&1&0&0\cr
                I&b&1-b&0\cr
                C'&0&a&1-a\cr}$$

La prima riga fornisce le etichette superiori, che appaiono sopra le grandi parentesi sinistro e destro; La prima colonna fornisce le etichette di sinistra, che sono a flush -flush a sinistra, poco prima della matrice stessa. L’elemento all’intersezione della prima colonna e la prima riga è normalmente vuota. E come \pmatrix,\Bordermatrix inserisce le sue parentesi.

Mettere le matrici nel testo di un paragrafo è generalmente sconsigliabile. Il motivo è che sono così grandi che sono meglio visualizzati. Ma comunque, potresti voler occasionalmente trascurarlo. In questo caso, puoi usare \scelto o`\inopplar:

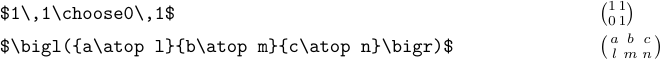
La macro \Matrix non produce piccoli array come questo.