7. Prestare le regolazioni al layout

Di solito, il LaTeX fa un ottimo lavoro nel presentare formule di matematica. Ma a volte è necessaria una regolazione più fine del posizionamento. Questo articolo discute alcune tecniche per mettere a punto il layout per migliorare le formule di matematica.

7.1. Dimensionamento automatico e spaziatura

I simboli e le lettere di matematica generalmente diventano più piccoli (e con una spaziatura più stretta), quando compaiono in frazioni, abbonamenti o apice. Le formule di matematica possono essere disposte in otto stili di matematica Tex:


D, D'	`\displaystyle`	Visualizzati singolarmente sulle righe
T, T'	`\textstyle`	Incorporati nel testo
S, S'	`\scriptstyle`	In apici o pedici
SS, SS'	`\scriptscriptstyle`	In tutti gli apici o pedici di ordine superiore

Lo stile di testo (t) è usato al livello superiore di una formula che è impostata in esecuzione del testo (tra una coppia di $ o tra $ e $), mentre lo stile di visualizzazione viene usato al livello superiore di una formula visualizzata (tra una coppia di $$ o tra \[ `` ] `). Per quanto riguarda le sotto-formule, lo stile può essere determinato dalla seguente tabella:


D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

Il prossimo esempio illustra i vari stili:

 1\normalsize                 %% Style:
 2\[ b                        %% D
 3    ^0                      %% S
 4   +                        %% D
 5   \frac{(k + p)            %% T
 6          _{j'}             %% S'
 7         % \displaystyle
 8         \pm                %% T [D]
 9         \frac{(f + q)      %% S [T]
10                ^{(pk)      %% SS [S]
11                   ^y       %% SS
12                   _{j'}}}  %% SS'
13              {(h + y)}}    %% S' [T']
14        {(l + q)            %% T'
15          ^{(pk)}}          %% S'
16\]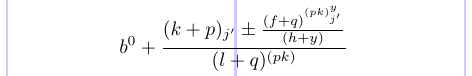

$Vari stili di matematica$

Puoi rimuovere il commento char (%) prima di \displaystyle e vedere come alcuni degli stili sono cambiati in quelli tra parentesi:

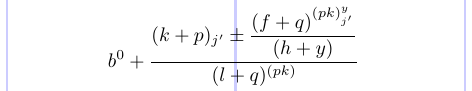
$Stili di matematica esplicitamente cambiati$

Mostra come specificare esplicitamente lo stile da utilizzare in ciascuna parte.

7.2. Sotto-forma

Nel testo, una coppia di parentesi graffe indica un gruppo o un ambito, all’interno del quale è in vigore una dichiarazione. All’interno di una formula matematica, inoltre delimitano una sotto-forma, che è sempre composta come un’entità separata che viene aggiunta alla formula esterna. Di conseguenza, le sotto-formule sono sempre composti alla loro larghezza naturale e non si allungano o si restringono orizzontalmente quando Tex costruisce un paragrafo che cerca di adattare la formula in una linea. Abbiamo già dimostrato che la sotto-forma da un semplice gruppo di tulioni viene elaborata come se fosse un singolo simbolo. Ciò significa che un gruppo vuoto produce un simbolo invisibile che può cambiare la spaziatura.

I contenuti di abbonamenti/apice e gli argomenti di molti (ma non tutti) comandi, come \frac e \mathrel, sono anche sotto-formule. Quindi, ottengono lo stesso trattamento speciale. L’argomento di \bm, ad esempio, non è necessariamente impostato come sotto-forma, e questa è una delle importanti eccezioni. In una formula matematica, se è necessario solo limitare l’ambito di una dichiarazione, definire un gruppo usando \begingroup e \endgroup. Ricorda che le dichiarazioni matematiche specializzate, come i cambiamenti di stile, si applicano fino alla fine dell’attuale sotto-forma, indipendentemente dal fatto che siano presenti altri gruppi.

7.3. Grandi delimitatori

Il LaTeX definisce quattro comandi - \big,\big, \bigg e bigg - per fornire il controllo diretto delle dimensioni dei delimitatori estensibili. Prendono un singolo argomento, che deve essere un delimitatore estensibile e produce versioni più grandi del delimitatore, da 1,2 a 3 volte la dimensione di base.

Ci sono anche tre varianti per ciascuno dei quattro comandi, dando quattro dimensioni di * Simbolo di apertura * (\bigl,\bigl, \biggl e \biggl); quattro dimensioni di * Simbolo di relazione * (\bigm,\bigm, \biggm e \biggm); e quattro dimensioni di * simbolo di chiusura * (\bigr,\bigr, \biggr e \biggr). Tutti i 16 di questi comandi devono essere usati con qualsiasi simbolo che può arrivare dopo \Left,\Right o (con etex) \Middle (vedi questa tabella).

Le dimensioni di questi delimitatori sono fissate nel LaTeX standard. Tuttavia, con il pacchetto amsmath, le dimensioni si adattano alle dimensioni del materiale circostante, in base alla dimensione del carattere e allo stile matematico in uso. Questo è mostrato nell’esempio seguente.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]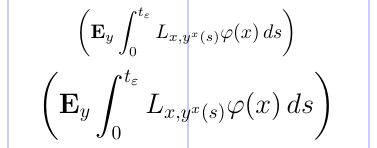

$Delimitatori che si adattano all’attuale dimensione del carattere e allo stile matematico$

7.4. Regolazione dell’indice su un radicale

Il posizionamento dell’indice su un segno radicale non è sempre buono nel LaTeX standard. Tuttavia, è possibile utilizzare i comandi \leftroot e \uproot definiti nel pacchetto amsmath per regolare il posizionamento di questo indice. Argomenti interi positivi a questi comandi spostano rispettivamente l’indice a sinistra e in alto, mentre gli argomenti negativi lo spostano a destra e in basso. Questi argomenti sono riportati in unità matematiche, che sono piuttosto piccole, quindi questi comandi sono adatti per la messa a punto.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4  \sqrt[\beta]{k} \qquad
5  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]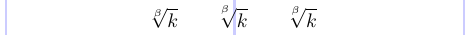

$Regolazione dell’indice di un segno radicale$

7.5. Perfezionamento con montanti e fantasmi

Ogni volta che si desidera “perfettamente” la spaziatura e l’allineamento della matematica, di solito è meglio rivolgersi a abilità uniche e avanzate di TEX primitivo. L’accesso a queste funzionalità è fornito da una serie di comandi relativi a \Phantom e \Smash. Tali comandi possono essere usati nelle formule matematiche o in testi in esecuzione.

Diamo un’occhiata al seguente esempio:

 1\usepackage{amsmath}
 2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
 3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
 4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
 5\newcommand\bfE{\mathbf{E}}
 6% -------------------------------------------------------------------------------
 7\begin{equation} \begin{split}
 8  f_{h, \ve}(x, y)
 9    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
10    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
11    &\relphantom{=} {} + h \biggl[
12       \frac{1}{\tve}
13       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
14               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
15    &\relphantom{=} \phantom{{} + h \biggl[ }
16       \frac{1}{\tve}
17       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
18               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19                                            \vf(x) \,ds    \biggr) \biggr]
20\end{split} \end{equation}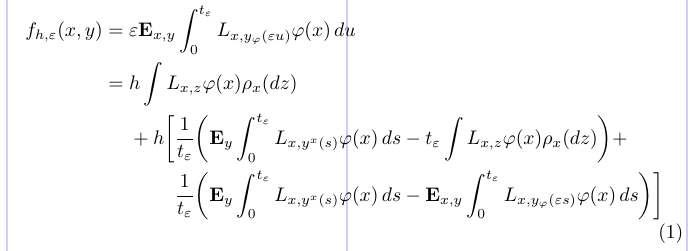

$I fantasmi della formula$

Qui, il comando \Phantom ottiene il posizionamento orizzontale regolato. Nel preambolo, viene utilizzato per definire un simbolo di relazione invisibile uguale in larghezza al suo argomento (= in questo esempio). All’interno degli ambienti di matematica, viene utilizzato per allineare determinate linee iniziandole con una “fantasma” o invisibile, sotto-forma. La coppia vuota di parentesi graffe {} è uguale a \Mathord {}, che produce un simbolo invisibile a larghezza zero necessaria per ottenere la spaziatura corretta di “+ *h *” (senza {}, il segno più produrrà un ulteriore plus unico con una spaziatura inappropriata prima *H *).

A differenza di \Phantom, il comando \smash compone il suo contenuto (in una scatola LR) ma quindi ignora sia la loro altezza che la loro larghezza, come se fossero entrambi zero. Il comando \hphantom, definito nel LaTeX standard, è una combinazione dei due. Produce l’equivalente di \Smash {\ Phantom {alcuni contenuti fantasma}}, ovvero una scatola invisibile con altezza e profondità zero ma la larghezza del contenuto di Phantom.

Il comando \vphanM è simile, ma rende la larghezza del fantasma zero preserva la sua altezza totale più profondità. Il comando \mathstrut è definito come\vphantom (e produce una scatola a larghezza zero di altezza e profondità uguale a quella di una parentesi.

Con il pacchetto amsmath, il comando \smash può sostenere un argomento opzionale, in modo che \smash [t] {...} ignori l’altezza del contenuto della scatola, mantenendo la profondità, mentre \Smash [b] {...} ignori la profondità, mantenendo l’altezza.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

$Distruggere l’espressione radicale$

Sembra che dare al y un po ‘di altezza extra con un montante renderà i radicali simili. Ma, invece, li rende solo più diversi e più brutti in tutto. Si scopre che distruggere il fondo del y è il modo migliore.

L’esempio seguente mostra un uso molto comune dello schianto. Il comando \Smash viene utilizzato lì per fornire un controllo fine sull’altezza dei delimitatori circostanti. Dimostra anche che lo schianto può causare problemi poiché è necessario conoscere la vera altezza della linea. Questo è riparato da \vphantom. \Hmjd è il simbolo composto definito come:

1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Per mostrare lo spazio verticale risultante abbiamo aggiunto regole:

Aspetto	`Codice`	Commento
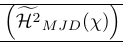$“Parentesi esterne troppo grandi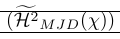”$	`\left( {\Hmjd } \right)`	Parentesi esterne troppo grandi
$“Parentesi esterne troppo piccole e righe troppo vicine”$	`\left( \smash{\Hmjd } \right)`	Parentesi esterne troppo piccole e righe troppo vicine
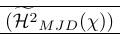$“Perfetto”$	`\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}`	Perfetto!
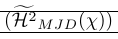$“Sono necessari sia Vphantom che Partial Smash”$	`\left( \smash[t]{\Hmjd } \right)`	Sono necessari sia `\vphantom` che Partial Smash

In alcuni punti, carenze nell’elaborazione TeX di basso livello possono causare errori nei dettagli più minuti della composizione. Ciò può accadere in layout particolari in cui (a) una sottoformula (numeratore/denominatore di una frazione o pedice/apice) consiste esattamente di un riquadro LR, o di un riquadro matematico costruito in modo simile, e inoltre (b) tale riquadro non ha le sue dimensioni naturali, come nel caso delle forme più complesse di \makebox, degli smash e di alcuni fantasmi.

Per vedere questo, diamo un’occhiata al seguente esempio:

1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]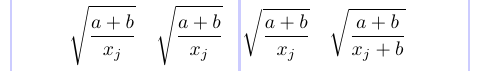

$Problemi causati dai frammenti$

Per ridurre la profondità del radicale, un \smash è stato aggiunto nel secondo radicale, ma questo non ha avuto alcun effetto. Nel terzo radicale, ha funzionato con un gruppo di bracciali vuoti. Ma nel quarto radicale, non era necessario un gruppo di tute vuote. Per riassumere, ogni volta che trovi \Smash non funziona, prova ad aggiungere una sotto-forma matematica vuota ({}) prima della scatola solitaria, per farlo trattare bene.

7.6. Spaziatura orizzontale

La messa a punto più fine e più difficile richiede i comandi di spaziatura espliciti mostrati nella tabella seguente:

$Comandi di spaziatura orizzontale$

Sia le forme complete che quelle brevi di questi comandi sono robuste e possono anche essere usate al di fuori delle formule di matematica nel testo normale. Sono correlati a spazi sottili, medi e spessi disponibili sulle macchine utilizzate per scrivere la matematica a metà del XX secolo.

I valori attuali dei tre parametri tex \thinmuskip,\medmuskip e \spessoremuskip definiscono la quantità di spazio aggiunta da questi comandi\.. spazio . I loro valori predefiniti con amsmath sono elencati nella tabella. Questi parametri di basso livello richiedono valori nelle unità matematiche (mu). Pertanto, possono essere impostati solo tramite incarichi di TEX di basso livello, non tramite \setLength o simili. Inoltre, normalmente i loro valori non dovrebbero essere modificati poiché vengono utilizzati internamente dalla composizione matematica di Tex (vedere la seguente tabella).

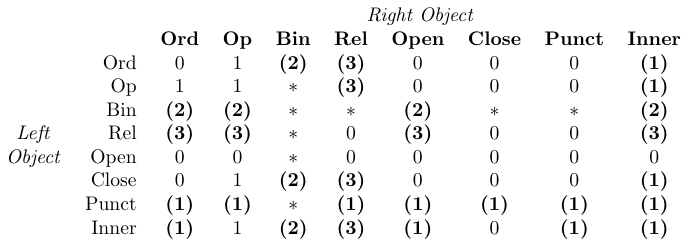
$Spaziatura tra simboli$

Nella tabella, 0 significa “nessuno spazio”, 1 significa \thinmuspace, 2 significa \medmuskip, 3 significa \thickmuskip, * significa “impossibile”. Le voci in grassetto indicano che la spaziatura corrispondente non viene aggiunta negli stili di scrittura matematica.

Un’unità di matematica (1mu) è uguale a 1/18 di un em nella dimensione dell’attuale carattere di matematica. Ne consegue che il valore assoluto di un mu varia con uno stile matematico, dando una spaziatura coerente indipendentemente dallo stile usato.

Testo nelle formule matematiche Caratteri di matematica in LaTeX