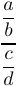5. Frazioni, coefficienti binomiali e stili di matematica
Un’altra cosa comune che potresti trovare nelle formule di matematica sono le frazioni e altre costruzioni in cui qualcosa come un numeratore è posizionato sopra qualcosa come un denominatore. Un esempio di quest’ultimo sono i coefficienti binomiali.
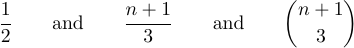
È possibile ottenere queste tre formule come equazioni visualizzate digitando $$ 1 \ over2 $$ e $$ n+1 \ over3 $$ e $$ \ n+1 \ scict3 $$.
Il comando \over si applica a tutto nella formula a meno che tu non lo racchiudica in una sottomissione specifica con parentesi graffe, nel qual caso\over si applica a tutto in quella sottomissione.

Non è possibile utilizzare \over due volte nella stessa sottomissione, cioè digitare a \ over b \ over 2. Invece, dovresti specificare esplicitamente ciò che accompagna cosa:

Sembra che entrambe le formule non abbiano un bell’aspetto. In tali casi, di solito è meglio convertire le frazioni in una “forma tagliata”. Ad esempio, le ultime due formule dovrebbero essere digitate come segue:
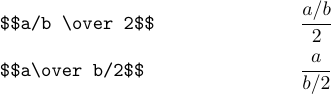
Ecco esempi più complessi:
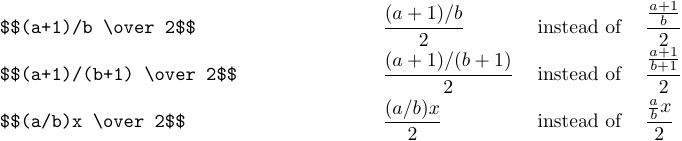
Guardando gli esempi sopra, potresti aver notato che le lettere e altri simboli a volte si riducono quando appaiono in frazioni, proprio mentre si riducono quando sono in abbonamenti o apice. Parliamo ora del modo in cui Tex sceglie le dimensioni dei simboli. Tex ha otto stili in cui può trattare le formule:
- Visualizza stile (per formule visualizzate su righe da sole)
- stile di testo (per formule incorporate nel testo)
- Stile di script (per subformule usate come apice o abbonamenti)
- Stile Scriptscript (per aprile o abbonamenti di secondo ordine) e quattro stili “angusti” che sono quasi gli stessi tranne che gli abbonamenti e i spietati non sono aumentati così tanto. Faremo riferimento agli otto stili come d, *d ’ *, *t *, *t’ *, s, *s ’ *, *ss *, *ss’ *, dove dè uno stile di visualizzazione, *d ’ *è uno stile di visualizzazione angusta, *t *è stile di testo, ecc. Tex usa anche tre dimensioni per digitare le formule matematiche: dimensione del testo, dimensione della sceneggiatura e scriptscript.
Per scrivere una formula nel testo in esecuzione, lo racchiude in $ ... $; Questo produce la formula con stile *t *. Oppure puoi racchiuderlo in $$ ... $$ per ottenere una formula visualizzata; Questo visualizza la formula con stile d. Le subformule di una formula possono essere in stili diversi. Una volta che conosci lo stile, puoi determinare le dimensioni del tipo che Tex utilizzerà:

Non esiste uno stile “sss” poiché tali piccoli simboli sarebbero ancora meno leggibili di quelli di Scriptscript.

For example, if x^{a_b} is to be typeset in style D, the a_b will be set in style S, and b in style SS; the result is
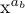
Non abbiamo ancora visto alcuna differenza tra gli stili d e t. C’è in realtà una leggera differenza nel posizionamento degli esponenti, sebbene in ciascun caso sia utilizzata la dimensione dello script. Ma c’è una grande distinzione tra gli stili d e t in caso di frazioni:

Quindi, se digiti $ 1 \ over2 $ (in un testo) ottieni stile sover style *s ’ *. Ma se digiti $$ 1 \ over2 $$ ottieni stile t over style * t ’ * in una formula visualizzata.
Infine, \sottoline non cambia lo stile. Accenti matematici e i comandi \sqrt e \overline cambiano stili non screpolati nei loro controparti anguste che mantengono stili angusti.
Può succedere che non ti piace lo stile che Tex seleziona in base alle sue regole. Sei libero di specificare lo stile desiderato digitando \displaystyle o\textstyle o \scriptstyle o\scriptscriptstyle; Lo stile selezionato si applicherà fino alla fine della formula o della subformance o fino a quando non si seleziona un altro stile. Ad esempio, $$ N+\ ScriptStyle n+\ ScriptscriptStyle n. $$ produce il seguente display:
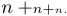
Mostra che anche il segno più si riduce man mano che lo stile cambia e che Tex non pone spazio + negli stili di sceneggiatura.
Diamo un’occhiata a un altro esempio: una frazione continua.
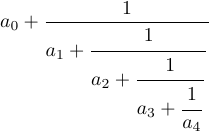
Puoi ottenerlo digitando
1$$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$$Senza \strut e \DisplayStyle in questa formula, il risultato sarebbe diverso:
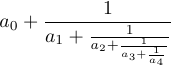
Latex definisce la macro \frac che consente di specificare le frazioni usando un’altra sintassi:\frac {a} {b} è equivalente a a \ over b e \frac12 è equivalente a 1 \ over2.
C’è un’altra operazione \in cima" in tex, che è come \over` tranne per il fatto che non disegna la linea di frazione:

Il formato in LaTeX definisce anche \scelto, che è come`\in cima ‘ma racchiude il risultato in parentesi:
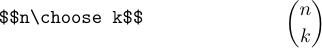
Si chiama \scelto perché è una notazione comune per il coefficiente binomiale che dice quanti modi ci sono di scegliere * k * cose da * n * cose.
I comandi \over,\inopp e \scelgono non possono essere miscelati tra loro. Ad esempio, $$ n \ Scegli k \ over 2 $$ è illegale. È necessario usare il raggruppamento per ottenere $$ {n \ Scegli k} \ over2 $$ o $$ n \ scelto {k \ over2} $$.
Tex ha il comando \sopra che è una versione generalizzata di\over e \inopp. In questo comando si specificano lo spessore esatto della regola della linea digitando \sopra <meen>. Per esempio,
1$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$Produrrà una frazione composta con una regola spessa 1pt tra le frazioni nel numeratore e il denominatore: