9. Simboli nelle formule di matematica

Le tabelle in questo articolo elencano la vasta gamma di simboli matematici forniti dai pacchetti AMS-Latex, compresi i comandi per accedere a ciascun simbolo. Includono anche i simboli supplementari del carattere St Mary Road progettato da Allan Jeffrey e Jeremy Gibbons. Questo pacchetto si estende Computer Modern e AMS Symbol Font Collections e normalmente dovrebbe essere caricato in aggiunta a “Amssymb`, ma sempre dopo. Fornisce simboli extra per campi come la programmazione funzionale, l’algebra di processo, la teoria del dominio, la logica lineare e molti altri.

Le tabelle indicano quali pacchetti extra devono essere caricati per utilizzare ciascun comando simbolo. I simboli con nomi di comandi in nero sono disponibili nel LaTeX standard. I simboli con nomi di comandi in blu richiedono il caricamento di amsmath, amssymb o stmaryrd. Se Nesessary, l’ulteriore classificazione viene data dai marcature: (stm) significa un simbolo di stmaryrd quando la tabella contiene anche simboli di altri pacchetti; e (var) segna “simboli alfabetici” (di tipo \mathalpha) che cambiano aspetto se usato all’interno dell’ambito di un identificatore di alfabeto matematico.

9.1. Classi di simboli matematica in LaTeX

La classificazione primaria dei simboli di matematica è legata al loro significato nell’uso tecnico. Nella tipografia matematica, questa classificazione definisce il layout della formula. In particolare, il formatter di matematica di Tex regola lo spazio orizzontale su entrambi i lati di ciascun simbolo in base alla sua classe matematica. Questa classificazione rende anche alcune distinzioni più belle, ad esempio tra accenti e simboli semplici e nel rompere l’enorme elenco dei simboli Relation in diverse tabelle.

L’impostazione per la matematica inserisce ciascun simbolo in uno di questi clasi: Ordinary (Ord), Operator (op), Binary (bin), Relation (rel), Opening (apertura), Closing (chiusura) o Punctuation (punct). La classe del simbolo può essere esplicitamente modificata usando i comandi \Mathord,\mathop, \mathbin,\mathrel, \mathopen,\mathopen e \mathpunct. Nel prossimo esempio, \# e \top (entrambi ord per impostazione predefinita) vengono modificati in un rel e un op.

\usepackage[fleqn]{amsmath}
\[ a \# \top _x^\alpha x^\alpha_b \]
\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]

Oltre alle classi di cui sopra, alcune sottoporme - soprattutto le frazioni e quelle prodotte da \left e \a destra - formano una classe chiamata *interiore *, che è esplicitamente disponibile tramite il comando \mathinner.

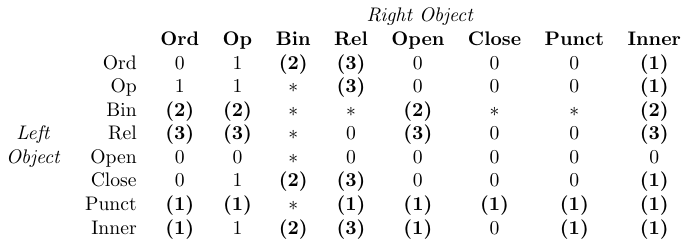
Nella tabella, “0” significa “nessuno spazio”, “1” significa \thinmuspace, “2” significa \medmuskip, “3” significa \thickmuskip, “*” significa “impossibile”. Le voci in grassetto indicano che la spaziatura corrispondente non viene aggiunta negli stili di scrittura matematici.

Tex gestisce la spaziatura all’interno delle formule semplicemente identificando la classe di ciascun oggetto in una formula e quindi aggiungendo spazio tra ciascuna coppia di oggetti adiacenti come definito dalla tabella precedente. Questa tabella è codificata nelle routine di composizione matematica di Tex e quindi non può essere modificata dai pacchetti macro.

Un simbolo Binary viene trasformato in un simbolo Ordinary ogni volta che non è preceduto e seguito da simboli di una natura compatibile con un’operazione binaria. Ecco perché alcune voci nel tavolo sono contrassegnate come impossibili. Ad esempio, $ +x $ dà +x(un unurario plus) e non +x. Quest’ultimo può essere prodotto da $ {}+x $.

Considera la seguente formula (i valori predefiniti vengono modificati per mostrare gli spazi aggiunti più chiaramente):

thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[
a - b = -\max \{ x , y \}
\]

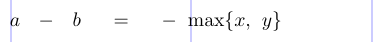
Tex identifica gli oggetti come Ord, Bin, Ord e così via, quindi inserisce gli spazi come segue:

 A      -      b      =      -    \max   \{   x    ,       y   \}
Ord \: Bin \: Ord \; Rel \; Ord \, Op   Open Ord Punct \, Ord Close

Il meno di fronte a \max viene trasformato in un *ordinario *perché un *binario *non può seguire una relazione.

In una costruzione “\a sinistra ... \ destra ”, l’intera sottoculale delimitata dalla costruzione diventa un singolo oggetto di classe *interno *. Al contrario, comandi come \bigl e \bigr producono simboli individuali delle classi *che si aprono * e *chiusura *, rispettivamente. La differenza tra loro viene rivelata nella tabella di spaziatura sopra. Sebbene possano provocare delimitatori di uguale dimensione verticale, possono sorgere differenze di spaziatura a seconda di oggetti adiacenti nella formula. Ad esempio, Ordinary seguito da * Apertura * non ottiene spazio, mentre Ordinary seguito da * interno * è separato da uno spazio sottile. Gli spazi all’interno della sottomissione all’interno di una costruzione “\a sinistra ... \ destra “sono fatti come previsto, a partire da un simbolo * di apertura * e terminano con un simbolo di chiusura *.

\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]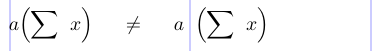

In sintesi, è meglio verificare che un simbolo appartenga alla classe desiderata, piuttosto che cercarlo nei tavoli che seguono.

9.2. Lettere, numeri e altri simboli * ordinari *

Le lettere latine ASCII non accentate e le cifre numeriche arabe sono tutte definite “simboli alfabetici”. Il carattere in cui sono digitati possono variare. Nelle formule di matematica, il carattere predefinito per le lettere latine è in corsivo, mentre per le cifre arabe è verticale/romano. I simboli alfabetici sono tutti di classe *ordinari *.

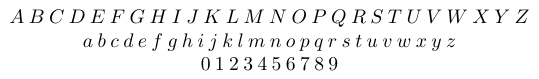
A differenza delle lettere latine, le lettere greche matematiche non sono più strettamente correlate ai glifi utilizzati per la composizione del testo greco normale. A causa di una curiosa evenienza del XVIII secolo, nella principale tradizione europea della tipografia matematica il carattere predefinito per le lettere greche minuscole nelle formule di matematica è in corsivo mentre per le lettere greche maiuscole è verticale/romano. (In fisica e chimica, ad esempio, le tradizioni tipografiche sono leggermente diverse.)

Le lettere greche capitali nelle prime righe della seguente tabella sono anche simboli alfabetici il cui carattere varia, con il valore predefinito verticale/romano. Ci sono lettere greche capitali, ognuna delle quali ha la stessa apparizione di una lettera latina (ad esempio, *a * e *alpha *, *b * e *beta *, *k * e *kappa , o * e *omicron *). Queste lettere non sono presenti nella tabella. Per lo stesso motivo, non esiste un omicron minuscolo. In pratica, le lettere greche che sembrano lettere latine non sono usate nelle formule di matematica.

I simboli in blu richiedono il pacchetto amssymb. ^(var) indica un simbolo alfabetico variabile.

La tabella successiva elenca altri simboli a forma di lettere della classe *ordinaria *. I primi quattro sono lettere ebraiche.

I simboli in blu richiedono il pacchetto amssymb.

La tabella successiva elenca i simboli rimanenti nella classe * ordinaria *, inclusa alcune punteggiature comuni. Questi si comportano come lettere e cifre, quindi non hanno mai spazio extra intorno a loro.

I simboli in blu richiedono il pacchetto amssymb o, se contrassegnati con ^(StM), il pacchetto stmaryrd.

Si noti che il punto esclamativo, il punto e il punto interrogativo non vengono considerati punteggiatura nelle formule.

Sinonimi: negazione logica - \lnot, \neg; | - \vert, |; || - \Vert, \|.

Un errore comune è usare questi simboli direttamente come operatori binari o simboli Relation, senza usare un comando di simbolo matematico correttamente definito per quel tipo. Pertanto, se usi comandi come \#, \Square o\& , controlla attentamente di ottenere gli spazi inter-simbolici corretti o, ancora meglio, definire il tuo comando di simbolo.

\usepackage[fleqn]{amsmath} \usepackage{amssymb}
\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
% -------------------------------------------------------------------------------
\[ a \neg b \qquad x \square y + z \]
\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
\[ a \bneg b \qquad x \rsquare y + z \]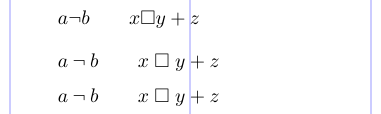

Il comando `\dichiarathsymbol” viene utilizzato per dichiarare il tuo nome di simbolo.

\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}

Il primo argomento è il nome del comando scelto. Il secondo argomento è uno dei comandi corrispondenti alla classe simbolo. Il terzo argomento identifica il carattere del simbolo da cui il simbolo dovrebbe essere recuperato. Il quarto argomento fornisce la posizione del simbolo nella codifica del carattere, un valore decimale, ottale o esadecimale. I valori corretti per gli argomenti potrebbero essere trovati più facilmente osservando le definizioni nel file amssymb.sty o fontmath.ltx (per i simboli fondamentali). Ad esempio, abbiamo cercato \neq e \Square, abbiamo sostituito il \Mathord in ogni caso e infine abbiamo dato un nuovo nome al simbolo risultante.

9.3. Accenti matematici

La tabella seguente elenca i comandi di accento disponibili nelle formule. La maggior parte di essi è definita in Tex standard. Vedi qui per informazioni sugli accenti estensibili. Quando aggiungi un accento matematico a un simbolo, il risultato è un simbolo della classe *ordinaria *.

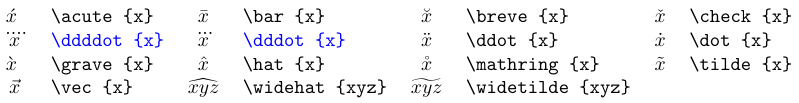
Gli accenti in blu richiedono il pacchetto amsmath.

Gli ultimi due accenti sono disponibili in diverse larghezze, e viene automaticamente utilizzato quello più grande.

\usepackage{amstext}
% -------------------------------------------------------------------------------
\[ a = b \text{ but } a \tilde{=} b
\text{ which is not } a \mathrel{\tilde{=}} b \]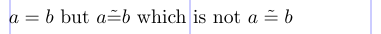

Altri modi per posizionare i simboli su Relazione I simboli sono mostrati qui. Quando si aggiunge un accento a un i o j in formule di matematica, è meglio usare le varianti senza punte \iMath e \jmath.

9.4. * Simboli dell’operatore binario*

Ci sono più di 100 simboli di classe binaria da cui scegliere. La maggior parte di loro è elencata nella tabella seguente. Alcuni di essi sono anche disponibili come simboli Relation, sebbene con nomi diversi.

I simboli in blu richiedono il pacchetto amssymb o, se contrassegnati con ^(StM), il pacchetto stmaryrd.

I triangoli sinistro e destro sono disponibili anche come simboli di Relazione.

Il pacchetto stmaryrd trasforma in modo poco chiaro i simboli binari \bigtriangleup e \bigtriangledown in Operatori, lasciando solo i sinonimi \varbigtriangleup e \varbigtriangledown per le forme operative binarie.

Il pacchetto Amssymb offre alcuni simboli di scatola da utilizzare come operatori Binary; Molti altri sono aggiunti da stmaryrd. Vedi il tavolo successivo.

Tutti i simboli richiedono il pacchetto amssymb oppure, se contrassegnati con ^(StM), il pacchetto stmaryrd.

È possibile caricare il pacchetto stmaryrd con l’opzionepesante. Di conseguenza, ogni comando del simbolo del cerchio dalla tabella successiva che inizia con \var scambia la sua definizione con il comando corrispondente senza” var “; Ad esempio, il simbolo \varodot diventa\odot e viceversa.

I simboli in blu richiedono il pacchetto amssymb o, se contrassegnati con ^(StM), il pacchetto stmaryrd.

L’opzione heavycircles del pacchetto stmaryrd ha effetto su tutti i comandi che iniziano con \var e sulle loro varianti normali.

9.5. Simboli di relazione

La classe di simboli binari Relation è persino grande di quella degli operatori Binary. La tabella successiva elenca i simboli per l’uguaglianza e l’ordine. Una barra può essere sottoposta a qualsiasi simbolo Relation precedendolo con il comando \not. Il simbolo negato rappresenta il complemento (o negazione) delle relazioni.

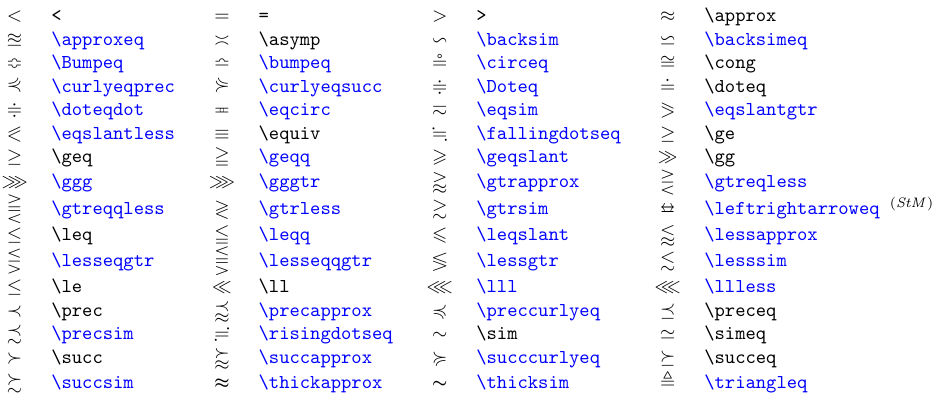
I simboli in blu richiedono il pacchetto amssymb oppure, se contrassegnati con ^(StM), il pacchetto stmaryrd.

$ u \not< v$ or $a \not\in \mathbf{A} $

Questo metodo generico per negare un simbolo Relation non dà sempre buoni risultati, specialmente con simboli più grandi, perché la barra sarà sempre delle stesse dimensioni, posizione e pendenza. Per questo fatto, sono disponibili anche alcuni “simboli negati” appositamente progettati. Vedi l’elenco nella tabella successiva.

I simboli in blu richiedono il pacchetto amssymb.

Se è disponibile una scelta, di solito è preferibile utilizzare i glifi appositamente progettati. Per capire perché, confronta i simboli nel prossimo esempio.

\usepackage{amssymb}
% -------------------------------------------------------------------------------
$ \not\leq \ \not\succeq \ \not\sim $ \par
$ \nleq \ \nsucceq \ \nsim $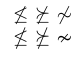

La tabella successiva elenca i simboli Relation per set e inclusioni.

I simboli in blu richiedono il pacchetto amssymb oppure, se contrassegnati con ^(StM), il pacchetto stmaryrd.

E ora negazioni dei simboli Relation per insiemi e inclusione.

I simboli in blu richiedono il pacchetto amssymb.

La tabella successiva elenca i simboli * Relazione * a forma di freccia. Alcune costruzioni di freccia estensibili che producono simboli di relazione composta * sono descritte qui.

I simboli in blu richiedono il pacchetto amssymb oppure, se contrassegnati con ^(StM), il pacchetto stmaryrd.

E qui ci sono i simboli negati a forma di freccia *.

I simboli in blu richiedono il pacchetto amssymb.

Esistono altri elementi (oltre a \not usati per annullare i simboli di relazione generale *) che erano appositamente progettati per negare o estendere i simboli simili a freccia. Vedi il tavolo successivo.

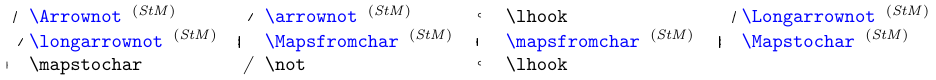
I simboli in blu richiedono il pacchetto stmaryrd.

Questi simboli servono per la combinazione, principalmente con le frecce; ad esempio, \longarrownot\longleftarrow.

Usa \joinrel per “incollare” insieme i simboli relazionali, ad esempio, \lhook\joinrel\longrightarrow.

Le dimensioni di questi simboli li rendono inadatti ad altri usi.

\usepackage{stmaryrd}
% -------------------------------------------------------------------------------
$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$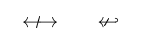

Infine, di seguito sono riportati altri simboli di relazione * Varie *.

I simboli di Relazione in blu richiedono il pacchetto amssymb.

\therefore è un simbolo di Relazione, quindi la sua spaziatura potrebbe non essere quella prevista negli usi comuni.