9. 表示された数式
これまでに個々の数式の扱い方について説明してきましたが、表示数式はしばしば多数の異なる数式や巨大な数式のさまざまな部分を含み、互いに正しく揃えるのは難しいことがあります。幸いなことに、大きな表示は一般にいくつかの単純なパターンに分類できます。
9.1. 1 行の表示
表示された数式には普通のテキストが含まれることがよくあります。すでに
discussed で、数式モードを抜けずにローマン体を取得する方法を説明しましたが、表示にテキストを入れる最善の方法は \hbox に入れることです。実は数式が全くなくても構いません。次のように書くことができます
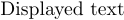
$\hbox{Displayed text}$。しかし、こちらはもう少し興味深い例です:

この場合、数式とテキストは次のように組み合わされています:
1$\X_n=X_k \qquad\hbox{if and only if}\qquad
2 Y_n=Y_k \quad\hbox{and}\quad Z_n=Z_k.$ご覧のように、\qquad は「if and only if」の前後に現れ、1 つの \quad が「and」の前後に配置されています。これにより、表示の Y と Z の部分が X の部分よりも互いにより密接に関連していることが強調されます。
以下の表示を見てみましょう:
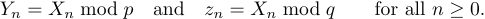
指定の一例は次のとおりです
1$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all }n\ge0.$しかし、2 行目を参照した方がよいでしょう(下のコード参照)
1$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all $n\ge0$.}$はい、これはディスプレイ数式モードの中に水平モードがあり、その中に数式モードがあるという構造ですが、最初の方法より自然に見えます。
次に、ディスプレイの横側に現れる小さなラベル、すなわち方程式番号について見てみましょう。次のように入力すると
1$<formula>\eqno<formula>$TeX は最初の数式を表示し、右端の余白に方程式番号(2 番目の数式)を付けます。例えば、
1$x^2-y^2 = (x+y)(x-y).\eqno(15)$は次のようになります。
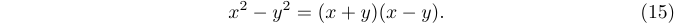
\leqno を使用すれば左側に番号を付けることもできます。例えば、
1$x^2-y^2 = (x+y)(x-y).\leqno(15)$は次のようになります。
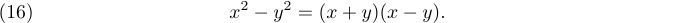
左側に表示される場合でも、番号は常に 2 番目に指定することに注意してください。
表示された方程式は、番号の有無に関わらず中央揃えになります。しかし、式が大きい場合、TeX は番号と衝突しないように配慮し、番号は単独の行に配置されることさえあります。
LaTeX は equation 環境を提供しており、式を自動的に番号付けできます。例えば次のように入力します
1\begin{equation}
2 f(x)=(x+a)(x+b)
3\end{equation}すると次のようになります。
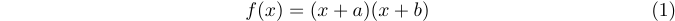
\label と \ref を使って式にラベルを付け参照することも可能です。例えば
1\begin{equation} \label{eq:someequation}
2 f(x)=(x+a)(x+b)
3\end{equation}
4this references equation \ref{eq:someequation}.は次のようになります。
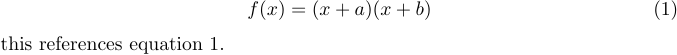
9.2. 複数行の表示
時には、1 行の数式(番号有無を問わず)の単純パターンに収まらない表示があります。LaTeX は残りの多くのケースに対して特別なコマンドを提供しています。
複数行の表示は通常、= 記号で揃える必要のある複数の式を含みます。例えば
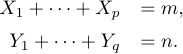
このような表示には、LaTeX が提供する array 環境を使用することが推奨されます。
1$\begin{array}{rl}
2 X_1+\cdots+\X_p&=m,\\
3 Y_1+\cdots+\Y_q&=n.}
4\end{array}$この環境は、式を 2 列(この例では 2 列)の長方形配列として表現するのに役立ちます。各行は \\(改行)で区切られた個別の式を含み、左側と右側は & 記号で分けられます。最後の行が \\ で終わっている必要はありません。各列の配置は環境の引数で指定でき、例では rl を指定しています。これは左側が右寄せ、右側が左寄せになることを意味します。
LaTeX は同様に動作する eqnarray* 環境も提供していますが、式の両側を正しく揃えるには 2 つの揃えポイントが必要で、残念ながら間隔が数式入力の慣例から外れてしまいます。次のコードは
1\begin{eqnarray*}
2 X_1+\cdots+X_p&=&m,\\
3 Y_1+\cdots+Y_q&=&n.
4\end{eqnarray*}次の出力を生成します。
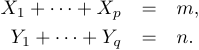
eqnarray 環境は同じ結果を出しますが、式に自動的に番号を付けます。
array 環境には任意の数の式を入れることができ、一般的なパターンは次のとおりです。
1\begin{array}{rl}
2 <left-hand side_1>&<right-hand side_1>\\
3 <left-hand side_2>&<right-hand side_2>\\
4 ...
5 <left-hand side_n>&<right-hand side_n>
6\end{array}ここで各 <right-hand side> は揃えたいシンボルで始まります。
array 環境の結果は上下方向にセンタリングされた箱になります。これにより次のような式を簡単に作れます。
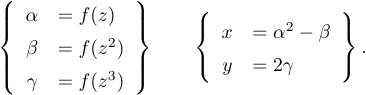
1$\left\{
2 \begin{array}{rl}
3 \alpha&=f(z)\\ \beta&=f(z^2)\\ \gamma&=f(z^3)
4 \end{array}
5\right\}\qquad\left\{
6 \begin{array}{rl}
7 x&=\alpha^2-\beta\\ y&=2\gamma
8 \end{array}
9\right\}.$次のレベルの複雑さは、複数の揃えられた式に複数の方程式番号が必要になる場合です。また、いくつかの行だけに番号を付け、他は付けない場合もあります。
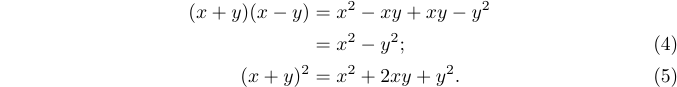
残念ながら、eqnarray* 環境(不適切な間隔あり)でも複数行ディスプレイに手動で方程式番号を指定する方法はありません。amsmath パッケージだけがこれを可能にします。したがって、上記の結果を得る推奨方法は次のとおりです。
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}align 環境の行で \tag と \notag の両方を省略すると、方程式番号は対応する内部カウンタの現在値を用いて自動的に生成されます。
amsmath パッケージを leqno オプション付きで読み込むと、方程式番号は左余白に表示されます。したがって
1%% Preamble
2\usepackage[leqno]{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}は次のようになります。
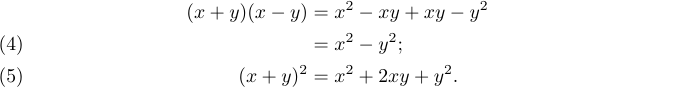
amsmath パッケージの機能を用いた数式組版の詳細については、これらの
記事 を参照してください。
9.3. 長い数式
ここでは、式が非常に長くて 1 行に収まらない場合にどうすべきかを議論します。例えば、次のような方程式があるとします。
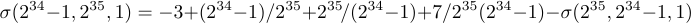
何らかの方法で分割する必要があります。TeX は + と - 記号の隣の空白をゼロに縮めてすべてを詰め込もうとしますが、それでも行がはみ出してしまいます。
+7 の直前で式を分割してみましょう。array 環境を多行式と同じように使用すると、= の右側に余分な空白が残ります。
1$\begin{array}{rl}
2 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
3 &\qquad{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1)
4\end{array}$したがって、再び amsmath パッケージを使用するのが最善です。しかし今回は式番号が不要なので align* 環境を使用すべきです。
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
6 &\qquad+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).
7\end{align*}$これにより次のようになります。
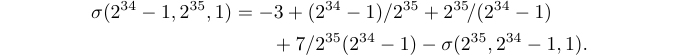
アイデアは、長い 1 行の式を 2 行の式として扱い、2 行目で \qquad を用いて 1 行目の = 記号の右側に十分な余白を確保することです。
長い表示数式をどのように改行すべきかを決めるのは実際には容易ではありません。TeX は自動的に改行を試みません。なぜなら、十分に汎用的な規則は存在しないからです。数式原稿の著者が最も適切な判断を下すべきで、改行位置は数式解説の微妙な要素に依存します。例えば、式の対称性や構造を強調したい場合があり、そのようなことは式が正確に何を表しているかを深く理解していることが前提となります。
それでも、長い表示数式を扱う際の経験則をいくつか挙げることは可能です。優れた数式組版者が従う原則がいくつかあります。
a) 段落内の数式は常に二項演算子や関係記号の後で改行されますが、表示数式は常に二項演算子や関係記号の前で改行されます。だから先ほどの例で最初の行を (2^{34}-1)+ で終わらせず、(2^{34}-1 で終わらせ、次の行を + で始めたわけです。
b) 式が二項演算子の前で改行される場合、2 行目は最も内側のサブ式がその二項演算子を含む位置から少なくとも 2 クアッド(約 2×字幅)右に開始すべきです。例えば、次のように + 記号で改行したいとします。
1$\sum_{0<k<n}\left(<formula_1>+<formula_2>\right)$このとき、+ 記号は左側の大きな括弧 \left( の右側に十分離れて配置するのがほぼ必須です。
この例では、 \left と \right デリミタは単独で使用できないため、2 行に分割するときは両方の行に対応するデリミタを揃えて同じサイズにする必要があります。通常は自分でデリミタのサイズを指定します。例えば \bigg デリミタを使うなら次のように書きます。
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sum_{0<k<n}\biggl(&<formula_1>\\
6 &\qquad+<formula_2>\biggr)
7\end{align*}この例では & マーカーは = 記号の位置ではなく、揃えたい位置を示すだけです。
別の方法として「2 行形式」と呼ばれる手法があります。最初の部分をほぼ左寄せにし、2 行目をほぼ右寄せ(「ほぼ左寄せ」=1 クアッド離す)に配置します。先ほどの長い sigma 式の 2 行形式は次の通りです。
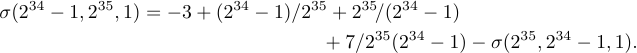
この 2 行効果を得るには次のように入力します。
1$\displaylines{\quad\sigma(2^{34}-1,2^{35},1)
2 =-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1)\hfill{}\cr
3\hfill{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).\quad\cr}$2 行目に余分な {} を入れたのは、TeX に + が二項演算子であることを認識させるためです。2 行形式は左辺が長い方程式に特に有用で、その場合は改行が等号の直前になるのが一般的です。