8。数学式の微調整|ラテックスマニュアル
私たちは、数式を構築するために必要な施設のほとんどについてすでに議論しています。しかし、本当に美しいフォーミュラを生成できるいくつかの素晴らしいポイント、あなたが入力する本や論文の全体的な外観と読みやすさを改善する式です。
8.1。句読点
一般的なルールは次のとおりです。フォーミュラの後に、コンマ、セミコロン、コロン、質問マーク、感嘆符などが続く場合、句がテキストにあるときに句の後に * $の後に配置します。しかし、式 *の前に句読点 *を $$の前に置きます。式が表示されたとき。例えば、
1If $x<0$, we have shown that $$y=f(x).$$したがって、ようなものを入力してはいけません
1for $x = a, b$, or $c$.そうあるべきです
1for $x = a$, $b$, $c$.最初のケースでは、Texは $ x = a、b $を単一の式としてタイプセットし、コンマと「b」の間に薄いスペースを置きます。単語間のスペースは常に薄いスペースよりも大きいため、このスペースはコンマと「C」の間のスペースと同じではありません。このような間隔は悪く見えますが、2番目のケースでは、間隔は見栄えがよくなります。
また、フォーミュラのコンマの後に壊れるのは通常、方程式 $ x = f(x、a)$のように間違っているため、コンマと「b」の間のスペースで段落の線を壊さないことも重要です。したがって、段落内のラインを破る可能性が抑制され、Tappetsetドキュメントの外観が悪化します。言い換えれば、句読点が式ではなく文に言語的に属している場合、「$ `」の外に置いておきます。
8.2。非アイタリック文字
「ログ」のような一般的な数学関数は、常にローマタイプで設定されます。このようなオブジェクトを式に含める最良の方法は、次のコマンドを使用することです。

次の例では、これらのコマンドのいくつかが使用されます。

最後の2つの表示式は、コマンドの一部が、合計記号のような制限を持つ大規模な演算子としてTexによって扱われていることを示しています。 \ maxの添え字は\ log の添え字のように扱われません。サブスクリプトと上付き文字は、\ det、 \ gcd、 \ inf、 \ lim、 \ liminf、 \ limsup、 \ max、 \ min、 \ pr、および \ sup、 \ sup、 \ supに添付されると制限になります。
上記の頻繁に使用される機能または演算子にローマタイプが必要な場合は、独自のコマンドを簡単に定義できます。制限付きのオペレーターを定義し、\oper と呼ぶとします。そのためには、次の定義を前文に含める必要があります。
1\def\oper{\mathop{\rm oper}}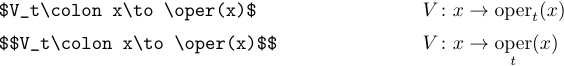
オペレーターに制限がないことが想定されていない場合は、次のような定義を使用してください。
1\def\oper{\mathop{\rm oper}\nolimits}単一の使用のためだけにローマタイプが必要な場合は、次のように「\ rm`タイプに切り替える方が簡単です。
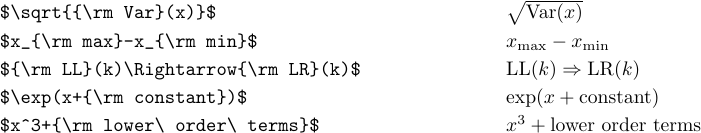
最後のケースでは「\」の使用に注意してください。それらがなければ、通常の空白は無視され、「下位条件」は「Lowerorderms」としてタイプセットされていたでしょう。
modという言葉は、一般的にフォーミュラのローマタイプで設定されているため、2つの異なる方法で使用されるため、より多くの注意が必要です。 LaTexは、 modがバイナリ操作である場合に使用する\ bmodコマンドを提供し、式の最後の括弧内で modが発生する場合に\ pmodコマンドが使用される場合に使用されます。

「\ pmodが独自の括弧を挿入することに注意してください。その括弧内の mod`の後に表示される量は、単一のシンボルでない限り、ブレースに囲まれる必要があります。
また、「\ rm」を使用して、ローマタイプを取得するのと同じ方法で、他のタイプのスタイルを入手することもできます。たとえば、 \ bfはboldfaceを与えます。

「+」と「=」がまだローマン体になっていることにお気づきでしょうか。LaTeXでは、\rmや\bfなどのコマンドは、大文字のAからZ、小文字のaからz、数字の0から9、ギリシャ文字の大文字の\Gammaから\Omega、そして数学記号の\hatや\tildeにのみ影響するように設定されています。ちなみに、$にはグループ化の効果があるため、この例では中括弧は使用されていません。\bfは現在のフォントを変更しますが、変更はローカルなものなので、数式外の現在のフォントには影響しません。
また、「書道」スタイルで大文字を取得するために、フォーミュラで「\ cal`」と言うこともできます。

これは
AからZまでの文字でのみ機能します。\calを小文字またはギリシャ文字に適用すると、奇妙な結果になります。
「Math Italic」の略である「\ mit」もあります。これは大手ギリシャ語に影響します。
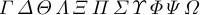
\ mitが有効になっている場合、通常の文字「a」から「z」と「a」は変更されません。それらは通常、数学のイタリックフォントから来ているため、通常どおり斜体で設定されています。逆に、大文字のギリシャ文字と数学のアクセントは、通常はローマのフォントから来ているため、「\ rm」の影響を受けません。
ラテックスを使用すると、「\ it」または \ ttを入力して、式で斜体またはタイプライターの文字を取得することもできます。なぜ「\ mit」と「\ it」の両方が提供されるのだろうと思うでしょう。答えは、「\ mit`は「数学イタリック」(通常は式に最適です)であり、「テキストのテキスト」(通常はテキストの実行に最適です)であるということです。
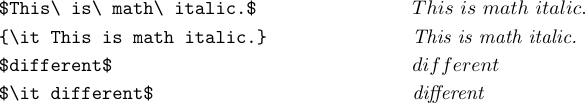
数学の斜体文字はより広く、間隔は異なります。これはほとんどの式でよりうまく機能しますが、数学モードで「differen」などの特定の斜体の単語を入力しようとすると、外観が低下します。通常、広い斜体「f」は式では望ましいものですが、テキストでは望ましいものではありません。したがって、実際のイタリック語を含むはずの式で「\ it`」を使用することが最善です。これは通常、古典的な数学の場合ではありませんが、コンピュータープログラムがタイプセットである場合によくあるケースです。

2番目の例は、識別子名を分割するための短い下線の使用を示しています。
8.3。式間の間隔
ディスプレイに複数の式が含まれている場合、一般的なケースです。たとえば、方程式には側条件を伴う場合があります。
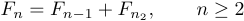
そのような場合、通常の慣習は物事を束ねるので、コンマの後にどれだけのスペースを置くかをテックスに伝える必要があります。これを取得するには、入力できます
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.ここでは、「\ qquad」は「ダブルクアッド」を表します。ここで、「クワッド」とは、プリンターに共通するある程度のスペースを意味します。したがって、 \ quadは、水平方向のプリンターの空間のクワッドを意味します。通常の規則とは異なる間隔が必要なときはいつでも、「Quad」や「\ qquad」などのコマンドを使用して明示的に指定する必要があります。
クワッドは、かつては幅1 em、高さ1Emの空白のタイプの正方形のピースでした。しかし、ラテックスのクワッドには高さはありません。
段落のテキストでは、式がコンマだけでなく、単語で区切られている場合、式はよりよく見えます。しかし、実際に挿入するテキストがない場合は、少なくとも式の間にスペースを置く必要があります。比較する
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.そして
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.与えるもの
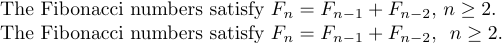
ここの「\」は、悪いスタイルを部分的に補う視覚的な分離を与えます。
8.4。式内の間隔
Texが数式の自動間隔を作っているため、ほとんどの場合に正しく見えるようになっていることがすでにわかりました。ただし、可能な式の数は巨大であり、Texの間隔ルールは非常に簡単であるため、例外が生じることは当然です。したがって、「\ 、 \ quad`、および「\ qquad」から生じる大きな部分の代わりに、そのようなケースの間隔の細かい単位があることが望ましいです。
テックスが式に入れる空間の基本的な要素は、 *薄いスペース *、 *中空間 *、および *厚い空間 *と呼ばれます。 Texはそれらを自動的に式に挿入しますが、コマンドを使用して、いつでも自分の間隔を追加できます

微積分を含む式は、 dxまたは dyまたは dの前に余分な薄いスペースが挿入されるときに最適に見えます。しかし、Texはこれを自動的に行いません。次の例は、これらのニーズについてTEXに伝える方法を示しています。

2番目の最後の式の「/」の後に「\、」が必要であったことに注意してください。また、 dtは分数の分子にすべてが表示されるため、最後の例では「\、 `が必要ありません。これにより、式の残りの部分から視覚的に剥離します。
物理ユニットは、フォーミュラに表示される場合、ローマタイプに設定し、前の材料から薄い空間によって分離する必要があります。

次の文字が文字、数字、または開口部の区切り文字である場合、感嘆符(要因操作)の後に薄いスペースも挿入する必要があります。
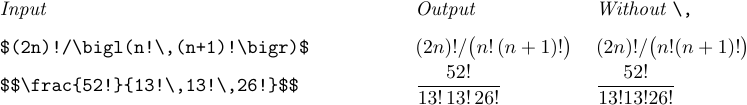
これらのケースに加えて、シンボルが強く束ねられすぎる、または形状の不運な組み合わせのために、あまりにも多くの空白が現れる式に遭遇することがあります。上品に適用された「\、 または \!」は、式の数学的重要性から読者が気を散らされないように、物事を開いたり、閉じます。ラジカルと複数の積分は、多くの場合、このような微調整の候補です。注意すべき状況の例をいくつか紹介します。

Texの間隔ルールは、「|」の場合に失敗することがありますと「\ |」これらのシンボルは、区切り文字としてではなく、通常のシンボルとして扱われるため、式に表示されます。式を考慮してください
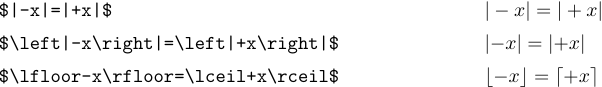
最初のケースでは、Texがプラス記号が「|」の合計を計算していると考えているため、間隔は間違っています。および ‘x’。 2番目の例で \ leftと \ rightを使用すると、Texは正しい軌道に乗っています。 3番目の例は、Texが開口部であるか閉鎖なのかを知っているため、他の区切り文字にはそのような修正は必要ないことを示しています。
8.5。楕円
楕円は、2つの異なる種類のドットで示すことができます。最良の伝統は、これら2つの可能性を区別します。一般的に、ような式を生成することは正しいです
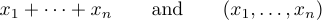
しかし、ような式を生成するのは間違っています
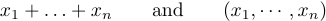
アイデアは、3つの低ドットが必要なときに \ ldotsを入力し、3つの垂直に中心のドットが必要な場合は「\ cdot」を入力することです。一般に、「+」と --と乗算標識の間で、および=signまたは"よりも少ない標識またはサブセットサインまたはその他の同様の関係の間でも「\ cdot」を使用することが最善です。コンマの間に低い点が使用され、物事が並置されている場合は、その間に兆候がまったくありません。
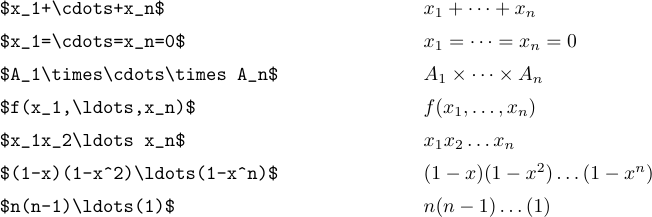
しかし、\ ldotsと \ cdotsが正しい間隔を生成しないという特別なケースがあります。これは、それらが式の最後に現れるとき、または閉じた区切り文字の直前に起こります。そのような状況では、余分な薄いスペースが必要です。たとえば、次の文章を検討してください。
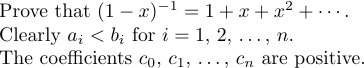
最初の文はタイピングによって作成されます
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.\がなければ、期間は「\ cdot」に近づきすぎていたでしょう。
2番目の文は次のように入力されました。
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.ネクタイ( 〜)の使用に注意してください。このような楕円は、ある形の数学的執筆で非常に一般的であるため、LaTexは「\ ldots \、$ の略語の略語として\ dots`マクロを段落のテキストで使用します。したがって、3番目の文を入力できます
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6。ラインブレイク
段落に式がある場合、Texは線の間でそれらを破壊する必要がある場合があります。関係記号の後、またはバイナリ操作シンボルの後にのみ式を破り、関係またはバイナリ操作は式の外側レベルにあります。これは、 {...}に囲まれていないことを意味します。たとえば、入力する場合
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$段落の途中で、= sign(優先)または - または +または - (緊急時)のいずれかの後にTexが壊れる可能性があります。しかし、いずれにしてもコンマの後に休憩はありません。なぜなら、その後のカンマが望ましいので、「$ `‘の間に壊れが望ましい」とは思わないからです。
=サインの後を除いて、この例を壊したくないので、入力できます
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$これらの追加ブレースはサブフォーミュラを「フリーズ」し、壊れない箱に入れます。しかし、Texが実際に式をひどく破っていない限り、このようなことを心配する必要はありません。
フォーミュラの外側レベルのある時点で壊れることを許可したい場合は、「\ approwbreak」と言うことができます。たとえば、式の場合
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$段落のテキストに表示されると、Texはそれを2つの部分に分割することを許可します
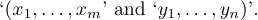
8.7。ブレース
シンボルの「{‘と’}」はさまざまな表記で使用され、LaTexはそのようなものを含む式に対処するのに役立つコマンドを提供します。 最も単純なケースは、ブレースが要素のセットを示すために使用される場合です。たとえば、「{a、b、c}」は、3つの要素a、b、およびcのセットを表します。
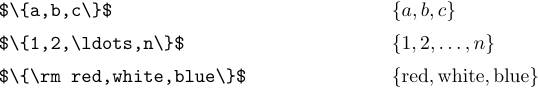
セットは、一般的な要素を与え、その後特定の条件を与えることによって示される場合があります。たとえば、5を超えるすべてのオブジェクト * x *のセットは、次のように書くことができます。

これらは、同じセットを示す2つのバリアントです。最初のものは、「\ mid」を使用して垂直バーを取得する必要がありますが、2番目のバーはバイナリ操作として扱われるコロン以外のものを必要としません。
区切り文字が大きくなる場合、\ bigl、 \ bigm、および \ bigrと呼ばれる必要があります。
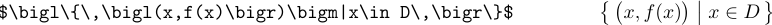
さらに大きな区切り文字を備えた式では、「\ bigまたは \ bigg」または\ biggコマンドを使用します。
また、表示された式でブレースの別の使用を見つけることもできます。実際には、多くの代替案の選択を示すのは、左のブレースです。
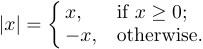
この構造は、コマンド「\ case」を使用して入力できます。
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$各ケースには、「&」シンボルで区切られた2つの部分があり、これは表形式構造の構築に特別な役割を果たします。 &の左側には、 $ ... $;に暗黙的に囲まれている数学の式があります。 &の右側は通常のテキストです。したがって、 -xでは、2行目では数学モードのタイプセットになりますが、「それ以外の場合」は水平モードでタイプセットになります。 「&」の前後の空白は無視されます。通常は2つしかありませんが、任意の数のケースがあります。各ケースの後に「\ cr」が続く必要があります。
コマンド「Overbrace」または「underbrace」を使用すると、水平ブレースは表示された式の一部または下に設定されます。そのようなことは「\ sum`のような大規模な演算子と見なされるため、上甘文字または添え字を指定することで、上または下に制限を設けることができます。

8.8。マトリックス
マトリックスは、数式のかなり一般的なオブジェクトです。それらは、行と列に配置された式の長方形の配列です。 LaTexは、最も一般的なタイプのマトリックスを扱うために「\ Matrix」コマンドを提供します。
たとえば、ディスプレイを指定すると仮定します
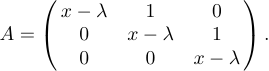
あなたがするのはタイプだけです
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$これは、以前に検討した「ケース」構造と非常によく似ています。マトリックスの各行は \ crによってフォロワーであり、& サインは各行の個々のエントリ間で使用されます。ただし、「\ cases」とは異なり、マトリックスの周りに自分の\ leftと \ rightのデリミターを置くことになっています。その理由は、異なるマトリックス構造で異なる区切り文字が使用される可能性があるためです。一方、括弧は他の区切り文字よりも頻繁に使用されるため、ラテックスに括弧を設定する場合は、「\ pmatrix」と入力できます。
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$マトリックスの各エントリは通常、その列の中心にあり、各列は含まれるエントリに対応するために必要なだけ拡張し、列間にスペースのクワッドがあります。列に左/右のフラッシュを出したい場合は、「\ hfill」に従ってください。
マトリックスの各エントリは、他のものとは別に処理され、テキストスタイルの数学式としてタイプセットです。したがって、たとえば、1つのエントリで「\ rm」と言うと、他のエントリには影響しません。 {\ rm x&y}を言うことは無効です。
行列は、省略された行や列を示すために省略記号を使用する一般的なパターンとしてよく使用されます。このような行列は、省略記号をそれぞれの行や列に配置することで組版できます。LaTeXでは、\ldotsに加えて、\vdots(縦線)と\ddots(斜め線)も用意されています。次の行列を考えてみましょう。
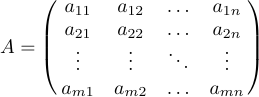
それは次のように指定されています:
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$マトリックスが上部に縁取られ、行と列にラベルを与える式で左に隣接している場合があります。この状況では、「\ bordermatrix」と呼ばれる特別なマクロがLaTexで定義されています。たとえば、ディスプレイ
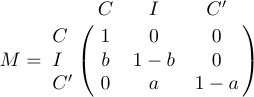
入力すると取得されます
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$最初の行は、大きな左右の括弧の上に表示される上部ラベルを与えます。最初の列は、マトリックス自体の直前に、タイプセットフラッシュ左に左ラベルを与えます。最初の列と最初の行の交差点の要素は通常空白です。そして、「\ pmatrix」のように、 \ bordermatrixは独自の括弧を挿入します。
段落のテキストにマトリックスを入れることは通常、めったにありません。その理由は、それらが非常に大きいので、よりよく表示されるからです。しかし、それでも、あなたは時々これを無視したいかもしれません。この場合、「\ choice」または \ atopを使用できます。
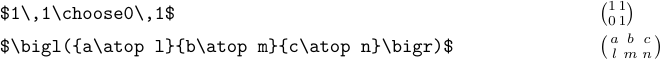
\ matrixマクロは、このような小さな配列を生成しません。