7. レイアウトの事前サイズ調整
通常、LaTeX は数式のレイアウトをうまく行いますが、場合によっては位置の微調整が必要になることがあります。本記事では、数式のレイアウトを若干改善するための微調整手法をいくつか紹介します。
7.1. 自動サイズ調整と間隔
数式記号や文字は、分数や下付き、上付きに現れるとき、一般に小さく(間隔も狭く)なります。数式は 8 種類の TeX 数学スタイルでレイアウトできます。
| D, D' | \displaystyle | Displayed on lines by themselves |
| T, T' | \textstyle | Embedded in text |
| S, S' | \scriptstyle | In superscripts or subscripts |
| SS, SS' | \scriptscriptstyle | In all higher-order superscripts or subscripts |
テキストスタイル (T) は、本文中に設定される数式の最上位レベルで使用されます(\( と \) の間、または \( ... \) のように)。一方、ディスプレイスタイルは、表示数式の最上位レベルで使用されます($ のペア、または \[ と \] の間)。副数式については、スタイルは以下の表から決定できます。
| D | S | S' | T | T' |
| D' | S' | S' | T' | T' |
| T | S | S' | S | S' |
| T' | S' | S' | S' | S' |
| S, SS | SS | SS' | SS | SS' |
| S’, SS' | SS' | SS' | SS' | SS' |
次の例は、さまざまなスタイルを示しています。
1\normalsize %% Style:
2\[ b %% D
3 ^0 %% S
4 + %% D
5 \frac{(k + p) %% T
6 _{j'} %% S'
7 % \displaystyle
8 \pm %% T [D]
9 \frac{(f + q) %% S [T]
10 ^{(pk) %% SS [S]
11 ^y %% SS
12 _{j'}}} %% SS'
13 {(h + y)}} %% S' [T']
14 {(l + q) %% T'
15 ^{(pk)}} %% S'
16\]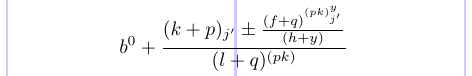
コメント文字 (%) を \displaystyle の前から削除すると、括弧内のスタイルが変わるのが確認できます。
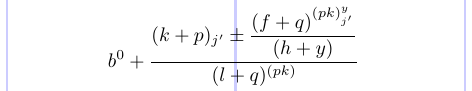
これは、各部分で使用するスタイルを明示的に指定する方法を示しています。
7.2. 副数式
本文中で波かっこ {} のペアは、ある宣言が有効になるグループ(スコープ)を示します。数式内では、これらはさらに副数式を区切ります。副数式は常に外側の式に追加される独立したエンティティとして組版され、その自然幅で出力され、TeX が段落を組んで行に収めようとした際に横方向に伸縮しません。単純な波かっこのグループから得られる副数式は、単一シンボルとして処理されることをすでに示しました。空のグループは、間隔を変えることができる見えないシンボルを生成します。
下付き・上付きの内容や \frac や \mathrel といった多くのコマンド(すべてではありません)の引数も副数式です。したがって、同じ特別な取り扱いを受けます。例えば \bm の引数は必ずしも副数式として設定されるわけではなく、これは重要な例外の一つです。数式内で宣言のスコープだけを限定したい場合は、\begingroup と \endgroup でグループを定義してください。スタイル変更などの特殊な数式宣言は、現在の副数式の終わりまで適用され、他のグループがあっても影響します。
7.3. 大きな区切り記号
LaTeX は四つのコマンド \big, \Big, \bigg, \Bigg を定義しており、伸張可能な区切り記号のサイズを直接制御できます。これらは単一の引数(伸張可能な区切り記号)を取り、基本サイズの 1.2 倍から 3 倍までの大きさの区切り記号を生成します。
さらに各コマンドには三つのバリエーションがあり、開く記号(\bigl, \Bigl, \biggl, \Biggl)、関係記号(\bigm, \Bigm, \biggm, \Biggm)、閉じる記号(\bigr, \Bigr, \biggr, \Biggr)の四サイズが提供されます。これら 16 個のコマンドは、\left, \right、または(eTeX では)\middle の後に続く記号とともに使用しなければなりません(この
表 を参照)。
標準 LaTeX ではこれらのサイズは固定されていますが、amsmath パッケージを使用すると、周囲の文字サイズや数式スタイルに合わせてサイズが自動的に調整されます。以下の例で示します。
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4 L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7 L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]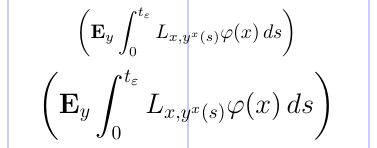
7.4. ルート記号のインデックス調整
標準 LaTeX では、根号のインデックス位置が必ずしも適切でないことがあります。amsmath パッケージで定義された \leftroot と \uproot コマンドを使用すれば、このインデックスの位置を微調整できます。正の整数引数はそれぞれ左へ、上へインデックスを移動させ、負の引数は右へ、下へ移動させます。これらの引数は数式単位で与えられ、非常に小さいため、細かい調整に適しています。
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4 \sqrt[\beta]{k} \qquad
5 \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6 \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]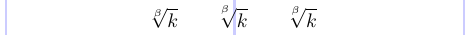
7.5. ストラットとファントムによる微調整
数式の間隔や配置を「完全に」整える必要がある場合、TeX のプリミティブが提供する高度な機能に頼ることが最善です。これらの機能は \phantom や \smash に関連する複数のコマンドで利用できます。これらのコマンドは数式内でも本文中でも使用できます。
以下の例を見てみましょう。
1\usepackage{amsmath}
2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
5\newcommand\bfE{\mathbf{E}}
6% -------------------------------------------------------------------------------
7\begin{equation} \begin{split}
8 f_{h, \ve}(x, y)
9 &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du \\
10 &= h \int L_{x, z} \vf(x) \rho_x(dz) \\
11 &\relphantom{=} {} + h \biggl[
12 \frac{1}{\tve}
13 \biggl( \bfE_{y} \int_0^{\tve} L_{x, y^x(s)} \vf(x) \,ds
14 - \tve \int L_{x, z} \vf(x) \rho_x(dz) \biggr) + \\
15 &\relphantom{=} \phantom{{} + h \biggl[ }
16 \frac{1}{\tve}
17 \biggl( \bfE_{y} \int_0^{\tve} L_{x, y^x(s)} \vf(x) \,ds
18 - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19 \vf(x) \,ds \biggr) \biggr]
20\end{split} \end{equation}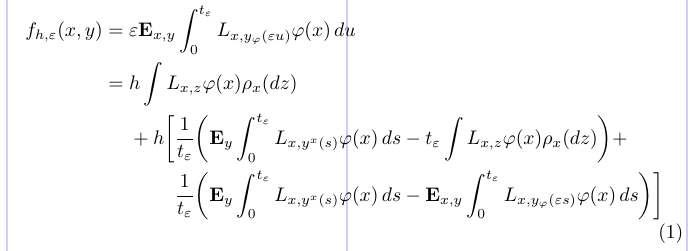
ここでは \phantom コマンドで水平位置を調整しています。前置き部で、引数と同じ幅の見えない関係記号(例では =)を定義しています。数式環境内では、行を「ファントム」すなわち見えない副数式で開始させることで特定の行を揃えます。空の波かっこ {} は \mathord{} と同等で、幅ゼロの見えないシンボルを生成し、+ h の間隔を正しく調整します。
\phantom とは対照的に、\smash は内容を LR ボックスに組んだ後、その高さと幅の両方を無視します(高さと幅がともに 0 であるかのように)。標準 LaTeX の \hphantom はこの二つを組み合わせたものです。\vphantom は幅を 0 に保ちつつ高さと深さは保持します。\mathstrut は \vphantom( と定義されており、括弧と同じ高さと深さのゼロ幅ボックスを生成します。
amsmath パッケージでは、\smash にオプション引数を付けられ、\smash[t]{...} は高さを無視し深さを保持し、\smash[b]{...} は深さを無視して高さを保持します。
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$
y にストラットで少し高さを与えると根号が似たように見えるように思えますが、実際には違いが際立ち、全体として見た目が悪くなります。y の下部をスマッシュするのが最も効果的です。
以下の例は、スマッシュの一般的な使用例を示しています。\smash は周囲の区切り記号の高さを細かく制御するために使用され、行の実際の高さが必要になる問題も \vphantom で修正できます。\Hmjd は次のように定義された複合記号です。
1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}結果の垂直空間を示すためにルールを追加しました。
| 外観 | Code | コメント |
|---|---|---|
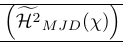 | \left( {\Hmjd } \right) | 外枠が大きすぎる |
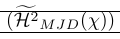 | \left( \smash{\Hmjd } \right) | 外枠が小さすぎてルールが近すぎる |
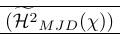 | \left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd} | ちょうど良い! |
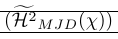 | \left( \smash[t]{\Hmjd } \right) | \vphantom と部分的な smash の両方が必要 |
いくつかのケースでは、低レベルの TeX 処理の欠陥が組版の微細なディテールにエラーを引き起こすことがあります。特に、(a)副数式がちょうど 1 つの LR ボックス(または同様に構成された数式ボックス)で構成され、そのボックスが自然サイズを持たない場合、(b)
\makebox、スマッシュ、いくつかのファントムなどの複雑な形態が関与する場合にこの問題が顕在化します。
これを確認するために、以下の例を見てみましょう。
1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]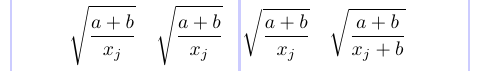
2 番目の根号に \smash を追加して深さを減らそうとしましたが、効果がありませんでした。3 番目の根号では空の波かっこグループを入れることで機能しましたが、4 番目の根号では空の波かっこは不要でした。要するに、\smash が機能しない場合は、孤立したボックスの前に空の数式副数式({})を挿入して正しく処理させてください。
7.6. 水平間隔
さらに細かく、かつ難しい調整には、以下の表に示す明示的な間隔コマンドを使用します。

これらのコマンドの全形・短形は堅牢で、数式外の通常テキストでも使用できます。20 世紀中頃に数学組版のために開発された薄・中・太スペースに由来しています。
3 つの TeX パラメータ \thinmuskip, \medmuskip, \thickmuskip の現在値が、これらの \..space コマンドが追加するスペース量を決定します。amsmath でのデフォルト値は表に示されています。これらの低レベルパラメータは数式単位(mu)で値を設定する必要があり、\setlength などでは設定できません。また、通常は TeX の内部数式組版が使用するため、変更すべきではありません(以下の表を参照)。
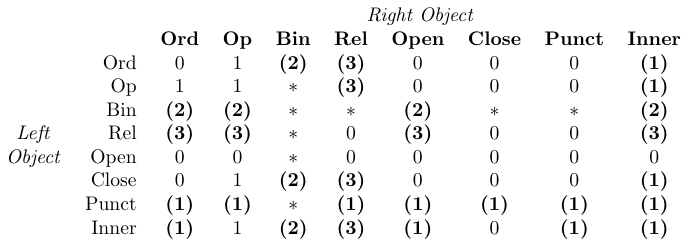
表では、0 が「間隔なし」、1 が
\thinmuspace、2 が\medmuskip、3 が\thickmuskip、* が「不可能」を意味します。太字で示されたエントリは、対応する間隔が数学スクリプトスタイルで追加されないことを示します。
1 mu は現在の数学フォントサイズの 1/18 em に相当します。したがって、mu の絶対値は数式スタイルに応じて変化し、スタイルが変わっても一貫した間隔が保たれます。