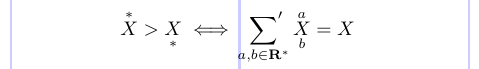4. Decorated symbols and compound structures | LaTeX manual

The amsmath package provides some commands to produce structures such as fraction-like objects and decorated symbols. This discusses covers some of them.

4.1. General fractions

The amsmath package defines the \genfrac command, which produces a generalized fraction.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

The first two arguments define left and right delimiters, respectively. Using the third argument, thick, you can override the default thickness of the fraction rule. For example, binominal coefficients (see below) use the value 0pt for this argument to make the line invisible. The default value (when left empty) of the line thickness is determined by the current font setup for math typesetting. The following list contains defaults used in the examples of this article.

Style	Default Thickness
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

The fourth argument, style, overrides (if not left empty) the math style for the layout and font size used. The value must be in the range 0-3: 0 - \displaystyle, 1 - \textstyle, 2 - \scriptstyle, 3 - \scriptscriptstyle. If this argument is left empty, the style is selected according to the normal rules for fractions. The last two arguments are the numerator and denominator.

The old fraction commands \over, \overwithdelims, \atop, \atopwithdelims, \above, and \abovewithdelims, which standard LaTeX inherits from TeX, produce warnings when they are used with the amsmath package.

4.1.1. Simple fractions

Having the \genfrac command, the amsmath package also defines three commands as convenient shorthands: \frac, \dfrac, and \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

The example below demonstrates the use of these commands:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.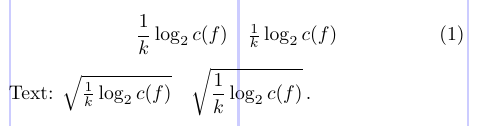

4.1.2. Binomial coefficients

Another fraction-like structure is binomial coefficients. To help you typeset them, the amsmath package provides similar commands \binom, \dbinom, and \tbinom.

This is how they abbreviate the \genfrac command:

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

And here’s the example:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.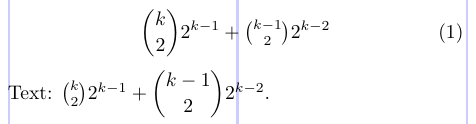

4.1.3. Continued fractions

If you need to typeset a fraction array, which is essentially an infinite fraction, also known as a “continued fraction”, there is the \cfrac command in the amsmath package. Pass the optional argument [l] or [r] to align a numerator to the left or to the right, which is centered by default.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}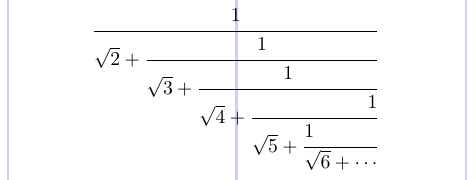

4.2. Boxed mathematics

The amsmath package provides the \boxed command similar to \fbox to put the math mode content into a box.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}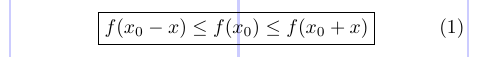

4.3. Positioning the limits

Subscripts and superscripts on integrals, sums, products, or other operators can be placed either above and below the math operator (the “limit position”) or in the subscript/superscript position on the right of the operator. Typically, limits are not used in text (otherwise the lines may spread). In a displayed formula, the placement depends on the operator. The following example shows the default placement in LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.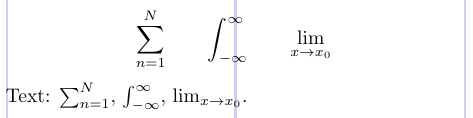

The amsmath package offers options for controlling the positioning. They are listed below, where default marks the behavior in case the amsmath package is used with a standard LaTeX document class but without any of these options.

intlimits, nointlimits	Place superscripts/subscripts of the integration symbols above and below or at the side (default), respectively. Used in displayed formulas only.
sumlimits, nosumlimits	Place superscripts/subscripts of large operators (sum, product, etc.) above and below (default) or at the side, respectively. Used in displayed formulas only.
namelimits, nonamelimits	Similar to sumlimits or nosumlimits but for certain operators, or “operator names”, such as inf, sup, lim, min, max, which are traditionally typeset with subscripts underneath, at least when they occur in a displayed formula.

TeX has three primitive commands that, appeared immediately after the symbol or operator name, control the positioning of subscripts/superscripts: \limits, \nolimits, and \displaylimits. The \displaylimits command produces subscripts/superscripts in the limit position when the current math style is a display style. This is the default behavior whenever a symbol of class Operator appears or a \mathop command is used. If you need to typeset an operator with subscripts/superscripts in the limit position outside a display, you must declare it individually using the \limits command.

Compare the following example to the previous one.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.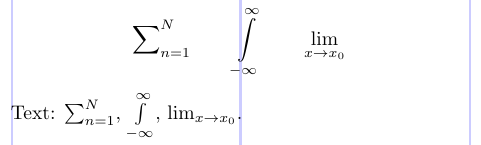

4.3. Multiple integrals

To typeset multiple integral signs with well-adjusted spaces between them in both text and displays, use the \iint, \iiint and \iiiint commands. The \idotsint produces two integral signs with ellipsis dots between them.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}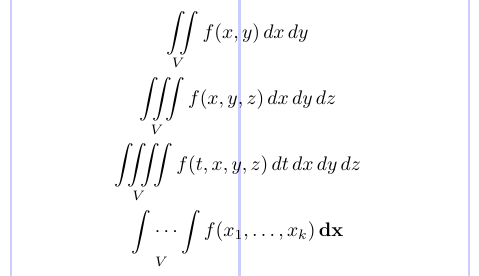

4.4. Modular relations

The “mod” notation for equivalence classes of integers is governed by the special spacing conventions. To deal with it, the amsmath package offers the \mod, \bmod, \pmod, and \pod commands. The following example shows the use of these commands.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}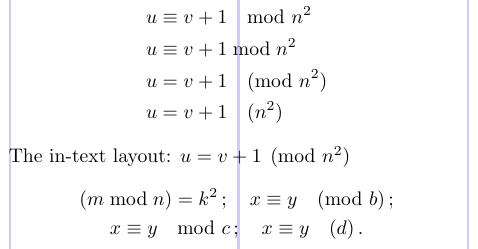

With amsmath, the spacing of \pmod is decreased within a non-displayed formula.

4.5. Mathematical dot accents

In addition to the \dot and \ddot math accents, the amsmath package provides the commands \dddot and \ddddot, which produce triple and quadruple dot accents, respectively.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Making superscripts from accents: the amsxtra package

The amsxtra package offers a useful feature, a collection of simple commands for placing accents as superscripts to subformula:

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$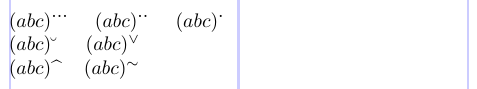

4.7. Other decorations

Standard LaTeX has the \stackrel command that places a superscript above a Relation symbol. In addition, the amsmath package defines the \overset and \underset commands. Use it to place material above or below any Ordinary or Relation symbol or Binary operator symbol.

The \sideset command adds decorations to any Operator symbol (sum, product, etc.) in addition to the normal limits. These are placed in the subscript and superscript positions to the left and right of the Operator.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]