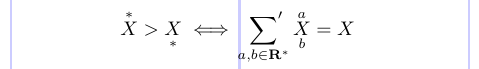4. Símbolos decorados e estruturas compostas

O pacote amsmath fornece alguns comandos para produzir estruturas como objetos semelhantes a fração e símbolos decorados. Isso discute cobre alguns deles.

4.1. FRAÇÕES GERAIS

O pacote amsmath define o comando \genFrac, que produz uma fração generalizada.

1\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Os dois primeiros argumentos definem delimitadores esquerda e direita, respectivamente. Usando o terceiro argumento, thick você pode substituir a espessura padrão da regra de fração. Por exemplo, os coeficientes binominais (veja abaixo) usam o valor 0pt para este argumento para tornar a linha invisível. O valor padrão (quando deixado vazio) da espessura da linha é determinado pela configuração atual da fonte para matemática. A lista a seguir contém padrões usados nos exemplos deste artigo.

Estilo	Espessura padrão
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

O quarto argumento, style, substitui (se não for deixado vazio) o estilo de matemática para o layout e o tamanho da fonte usado. O valor deve estar no intervalo 0-3: 0 - \displayStyle, 1 -\textStyle, 2 - \scriptStyle, 3 -\scriptScriptStyle. Se esse argumento for deixado vazio, o estilo será selecionado de acordo com as regras normais para as frações. Os dois últimos argumentos são o numerador e o denominador.

Os antigos comandos de fracção \over, \overwithdelims, \atop, \atopwithdelims, \above e \abovewithdelims, que o LaTeX padrão herda do TeX, produzem avisos quando são utilizados com o pacote amsmath.

4.1.1. Frações simples

Tendo o comando \genFrac, o pacote amsmath também define três comandos como uma taquigrafia conveniente: \frac, \dfrac e \tfrac.

1\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
2\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
3\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

O exemplo abaixo demonstra o uso desses comandos:

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \frac{1}{k} \log_2 c(f)
5  \quad \tfrac{1}{k} \log_2 c(f)
6\end{equation}
7Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
8        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.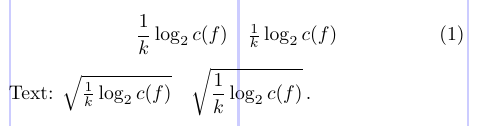

$\ frac, \ dfrac e \ tfrac$

4.1.2. Coeficientes binomiais

Outra estrutura semelhante a uma fração são os coeficientes binomiais. Para ajudá -lo a digitar, o pacote amsmath fornece comandos semelhantes \binom, \dbinom e \tbinom.

É assim que eles abreviam o comando \genFrac:

1\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
2\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
3\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

E aqui está o exemplo:

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
5\end{equation}
6Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.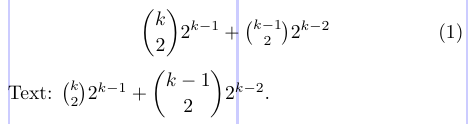

$\binom, \dbinom e \tbinom$

4.1.3. Frações contínuas

Se você precisar compensar uma matriz de fração, que é essencialmente uma fração infinita, também conhecida como “fração contínua”, existe o comando \cfrac no pacoteamsmath. Passe o argumento opcional [l] ou [r] para alinhar um numerador à esquerda ou à direita, que é centralizada por padrão.

 1\usepackage{amsmath}
 2% -------------------------------------------------------------------------------
 3\begin{equation*}
 4\cfrac {1}{\sqrt{2} +
 5  \cfrac {1}{\sqrt{3} +
 6    \cfrac {1}{\sqrt{4} +
 7      \cfrac[r] {1}{\sqrt{5} +
 8        \cfrac[l] {1}{\sqrt{6} + \dotsb }
 9}}}}
10\end{equation*}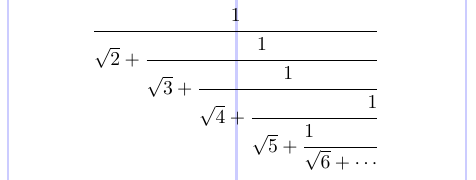

$Uma fração contínua$

4.2. Matemática em caixa

O pacote amsmath fornece o comando \boxed semelhante ao \fbox` para colocar o conteúdo do modo matemático em uma caixa.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
5\end{equation}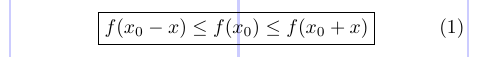

$Uma fórmula em caixa$

4.3. Posicionando os limites

Subscritos e superscritos em integrais, somas, produtos ou outros operadores podem ser colocados acima e abaixo do operador de matemática (a “posição limitada”) ou na posição de subscrito/substituto à direita do operador. Normalmente, os limites não são usados no texto (caso contrário, as linhas podem se espalhar). Em uma fórmula exibida, a colocação depende do operador. O exemplo a seguir mostra o posicionamento padrão no LATEX.

1\[
2\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
3\]
4Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.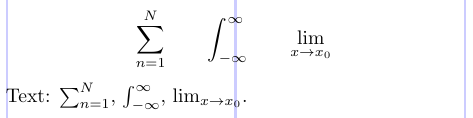

$O posicionamento padrão dos subscritos/superscripts no LaTeX$

O pacote amsmath oferece opções para controlar o posicionamento. Eles estão listados abaixo, onde * padrão * marca o comportamento caso o pacote amsmath seja usado com uma classe padrão de documentos de LaTeX, mas sem nenhuma dessas opções.


`intlimits`, `nointlimits`	Posiciona sobrescritos/subscritos dos símbolos de integração acima e abaixo ou ao lado (padrão), respetivamente. Utilizado apenas em fórmulas exibidas.
`sumlimits`, `nosumlimits`	Posiciona sobrescritos/subscritos de operadores grandes (soma, produto, etc.) acima e abaixo (padrão) ou ao lado, respetivamente. Utilizado apenas em fórmulas exibidas.
`nomelimites`, `nonamelimits`	Semelhante aos `sumlimits` ou `nosumlimits`, mas para certos operadores, ou “nomes de operadores”, como `inf`, `sup`, `lim`, `min`, `max`, que são tradicionalmente compostos com subscritos abaixo, pelo menos quando ocorrem numa fórmula apresentada.

A TEX possui três comandos primitivos que, apareceram imediatamente após o nome do símbolo ou operador, controlam o posicionamento de subscritos/superscritos: \Limits, \nolimits e \DisplaylImits. O comando \DisplaylIlits produz subscritos/superscripts na posição limitada quando o estilo de matemática atual é um estilo de exibição. Este é o comportamento padrão sempre que um símbolo do operador de classe * aparece ou um comando \Mathop é usado. Se você precisar digitar um operador com subscritos/superestritos na posição limitada fora de uma tela, deverá declará -lo individualmente usando o comando \limits.

Compare o exemplo a seguir com o anterior.

1\[
2\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
3\]
4Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.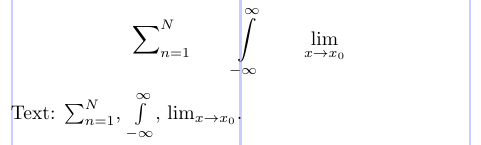

$Controlando a colocação dos subscritos/superescrits com as primitivas TEX$

4.3. Múltiplas integrais

Para digitar vários sinais integrais com espaços bem ajustados entre eles no texto e nos monitores, use os comandos \iint, \iiint e \iiiint. O \iDotsint produz dois sinais integrais com os pontos de elipse entre eles.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{gather*}
4\iint \limits _V f(x,y) \,dx \,dy \\
5\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
6\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
7\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
8\end{gather*}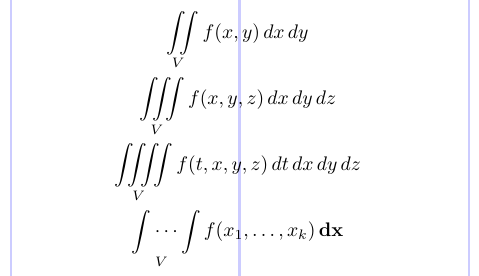

$Múltiplas integrais$

4.4. Relações modulares

A notação “mod” para as classes de equivalência de números inteiros é governada pelas convenções de espaçamento especiais. Para lidar com isso, o pacote amsmath oferece os comandos\mod, \bmod, \pmod e \pod. O exemplo a seguir mostra o uso desses comandos.

 1\usepackage{amsmath}
 2% -------------------------------------------------------------------------------
 3\begin{align*}
 4u & \equiv v + 1 \mod{n^2} \\
 5u & \equiv v + 1 \bmod{n^2} \\
 6u & = v + 1 \pmod{n^2} \\
 7u & = v + 1 \pod{n^2}
 8\end{align*}
 9The in-text layout: $ u = v + 1 \pmod{n^2} $
10\begin{gather*}
11(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
12x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
13\end{gather*}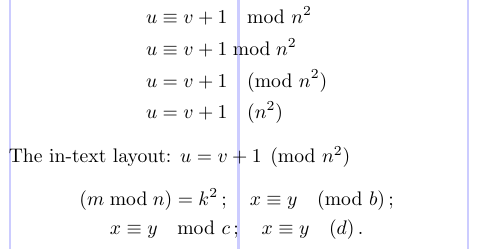

$Relação modular$

Com amsmath, o espaçamento de \pmod é diminuído dentro de uma fórmula não apresentada.

4.5. Acentos matemáticos do ponto

Além dos detalhes em matemática \dot e \ddot, o pacote amsmath fornece os comandos\dddot e \ddddot, que produzem detalhes em pontas triplas e quadruplas, respectivamente.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

$Acentos do ponto$

4.6. Fazendo superestritos da Acentos: o pacote `amsxtra`

O pacote AMSXTRA oferece um recurso útil, uma coleção de comandos simples para colocar sotaques como superestritos na subformula:

1\usepackage{amsxtra}
2% -------------------------------------------------------------------------------
3$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
4$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
5$(abc)\sphat$ \quad $(abc)\sptilde$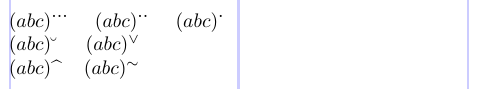

$Acentos como superscritos$

4.7. Outras decorações

O LATEX padrão possui o comando \Stackrel que coloca um superestrado acima de um símbolo Relation . Além disso, o pacote AMSMATH define os comandos \overset e \UnderSet. Use -o para colocar o material acima ou abaixo de qualquer símbolo Ordinary ou Relation ou Operador Binário.

O comando \sideetadiciona decorações a qualquer símbolo Operator (soma, produto, etc.), além dos limites normais. Estes são colocados nas posições subscritas e superscritões à esquerda e à direita do Operator.

1\[ \overset{*}{X} > \underset{*}{X}
2\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
3\overset{a}{\underset{b}{X}} = X \]

$Mais decoração$

Matriz e ambientes semelhantes Símbolos extensíveis e ajustáveis