9. Equações exibidas
Até agora, discutimos como lidar com fórmulas individuais; Mas as exibições geralmente envolvem um monte de fórmulas diferentes, ou peças diferentes de uma fórmula enorme, e pode ser um desafio colocá -las para que elas se alinhem corretamente. Felizmente, exibições grandes geralmente se enquadram em alguns padrões simples.
9.1. Exibições de uma linha
As equações exibidas geralmente contêm texto comum. Já discutimos (1) como colocar o tipo romano em fórmulas sem sair do modo de matemática, mas a melhor maneira de colocar texto em uma tela é colocá -lo em um \hbox. Na verdade, nem precisa haver nenhuma matemática. Para digitar o conjunto
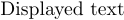
Você pode dizer $$ \ hbox {texto exibido} $$. Mas aqui está um exemplo mais interessante:

Nesse caso, fórmulas e texto foram combinados da seguinte forma:
1$$\X_n=X_k \qquad\hbox{if and only if}\qquad
2 Y_n=Y_k \quad\hbox{and}\quad Z_n=Z_k.$$Como você pode ver, \qquad aparece em torno de" se e somente se “, mas um único \quad arredores “e”; Isso levanta o sotaque do fato de que as partes y e z da tela estão mais relacionadas uma da outra do que a parte x.
Vejamos a seguinte tela:
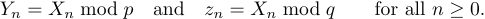
Uma maneira de especificar é
1$$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all }n\ge0.$$Mas a melhor maneira seria (veja a segunda linha)
1$$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all $n\ge0$.}$$Sim, esse é o modo de matemática dentro do modo horizontal dentro do modo de matemática de exibição, mas essa solução parece mais natural que a primeira.
Agora, vamos recorrer a números de equações, aqueles pequenos rótulos que aparecem ao lado dos monitores. Se você digitar
1$$<formula>\eqno<formula>$$A Tex exibirá a primeira fórmula e também colocará um número da equação (a segunda fórmula) na margem direita. Por exemplo,
1$$x^2-y^2 = (x+y)(x-y).\eqno(15)$$produzirá
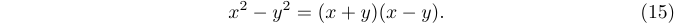
Você também pode obter números de equação na margem esquerda usando \leqno. Por exemplo,
1$$x^2-y^2 = (x+y)(x-y).\leqno(15)$$produzirá
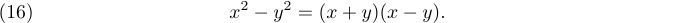
Observe que você sempre dá o número do número da equação, mesmo quando ela aparecerá à esquerda.
As equações exibidas são centralizadas independentemente da presença dos números de equação. Mas quando uma fórmula é grande, a TEX garante que não interfira em seu número; O número da equação pode até ser colocado em uma linha por si só.
O LATEX também fornece o ambiente da equação para numerar automaticamente suas equações. Por exemplo, digitando
1\begin{equation}
2 f(x)=(x+a)(x+b)
3\end{equation}resulta em
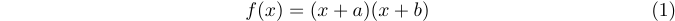
Também é possível rotular e referenciar equações usando \label e \ref. Por exemplo,
1\begin{equation} \label{eq:someequation}
2 f(x)=(x+a)(x+b)
3\end{equation}
4this references equation \ref{eq:someequation}.resulta em
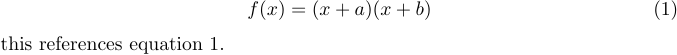
9.2. Displays multi-lines
Às vezes, uma tela pode não se encaixar no padrão simples de uma fórmula de uma linha com ou sem um número da equação. O LATEX fornece comandos especiais para a maioria dos casos restantes.
Telestas multi-lines geralmente incluem várias equações que devem ser alinhadas por seus sinais ‘=’, como em
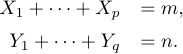
O método recomendado para tal exibição é usar o ambiente Array fornecido pelo LATEX:
1$$\begin{array}{rl}
2 X_1+\cdots+\X_p&=m,\\
3 Y_1+\cdots+\Y_q&=n.}
4\end{array}$$Esse ambiente ajuda você a representar suas equações como uma matriz retangular de várias colunas (duas colunas neste caso). As linhas contêm equações individuais separadas pelo comando \\ (que é uma nova linha). Os lados esquerdo e direito de cada equação são separados pelo símbolo &. Não é necessário que a última linha termine com \\. O ambiente também tem um argumento que especifica o alinhamento em cada coluna. No exemplo, o valor apropriado é rl, o que significa que os lados esquerdo das equações saem da direita, enquanto os lados da direita sairão nivelados à esquerda.
O LATEX também fornece o ambiente eqNarray* que funciona da mesma forma, mas para que os dois lados das equações alinhem adequadamente, ele precisa de dois pontos de alinhamento e, infelizmente, o espaçamento se torna um pouco fora das convenções de digitação matemática. O código a seguir
1\begin{eqnarray*}
2 X_1+\cdots+X_p&=&m,\\
3 Y_1+\cdots+Y_q&=&n.
4\end{eqnarray*}produz a seguinte saída:
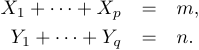
O ambiente eqNarray do LATEX produz o mesmo resultado, exceto que ele automaticamente numeram as equações.
Pode haver várias equações em um ambiente Array; O padrão geral é
1\begin{array}{rl}
2 <left-hand side_1>&<right-hand side_1>\\
3 <left-hand side_2>&<right-hand side_2>\\
4 ...
5 <left-hand side_n>&<right-hand side_n>
6\end{array}onde cada lado <à direita> começa com o símbolo no qual você deseja que o alinhamento ocorra.
O resultado do ambiente Array é uma caixa verticalmente centrada. Isso facilita a obtenção de uma fórmula como
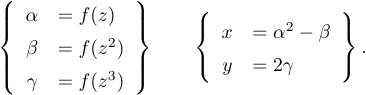
Você simplesmente usa o ambiente Array duas vezes na linha:
1$$\left\{
2 \begin{array}{rl}
3 \alpha&=f(z)\\ \beta&=f(z^2)\\ \gamma&=f(z^3)
4 \end{array}
5\right\}\qquad\left\{
6 \begin{array}{rl}
7 x&=\alpha^2-\beta\\ y&=2\gamma
8 \end{array}
9\right\}.$$O próximo nível de complexidade ocorre quando você tem várias equações alinhadas com vários números de equações. Ou algumas das linhas podem ser numeradas e outras não:
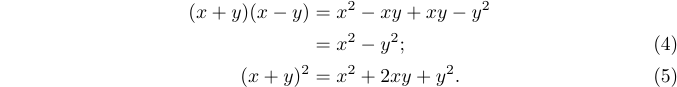
Infelizmente, mesmo com o ambiente eqNarray* (com seu espaçamento inadequado), não há como especificar manualmente os números de equações em uma tela de várias linhas. Somente o pacote amsmath pode
ajuda. Portanto, a maneira recomendada de obter o resultado acima é digitar:
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}Se você omitir \tag e \notag em uma linha do ambiente `alinhado ‘, o número da equação será gerado automaticamente usando o valor atual armazenado no contador interno correspondente.
Se você carregar o pacote amsmath com a opção leqno, os números da equação aparecerão na margem esquerda. Por isso
1%% Preamble
2\usepackage[leqno]{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}produz
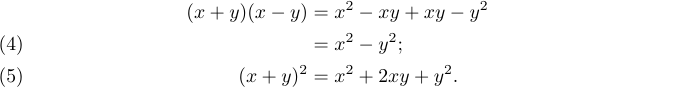
Para saber mais sobre as fórmulas de matemática com tipo de composição usando os recursos do pacote amsmath, consulte esses
artigos.
9.3. Fórmulas longas
Agora, vamos discutir o que deve ser feito quando uma fórmula é tão longa que não se encaixa em uma única linha. Por exemplo, suponha que você encontre a equação
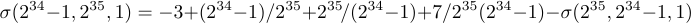
Você terá que quebrá -lo de alguma forma; A Tex fez o possível para espremer tudo, encolhendo os espaços ao lado de ‘+’ e ‘-’ signos para zero, mas ainda assim a linha ficou muito cheia.
Vamos tentar quebrar essa equação antes do ‘+7’. O ambiente Array deixa muito espaço à direita do ‘=’ se você o usar da mesma maneira que para equações de várias linhas:
1$$\begin{array}{rl}
2 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
3 &\qquad{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1)
4\end{array}$$Portanto, é melhor recorrer ao pacote Amsmath novamente. Mas desta vez você deve usar a matriz alinhada*, pois os números da equação não são necessários:
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
6 &\qquad+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).
7\end{align*}$$Isso rende
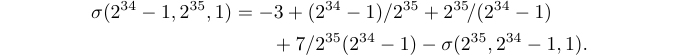
A idéia é tratar uma fórmula de uma linha longa como uma fórmula de duas linhas, usando \qquad na segunda linha, para que a segunda parte da fórmula pareça bem à direita do sinal ‘=’ na primeira linha.
Na verdade, não é uma tarefa fácil decidir como quebrar fórmulas longas exibidas em linhas; A Tex nunca tenta fazer isso, porque nenhum conjunto de regras é realmente adequado. O autor de um manuscrito matemático é geralmente o melhor juiz do que fazer, pois as posições de quebra dependem de fatores sutis de exposições matemáticas. Por exemplo, muitas vezes é desejável enfatizar parte da simetria ou outra estrutura subjacente à fórmula, e essas coisas exigem uma sólida compreensão do que exatamente está acontecendo nessa fórmula.
No entanto, é possível declarar algumas regras de polegar sobre como lidar com fórmulas longas em exibições, pois existem alguns princípios de que o melhor tipador matemático tende a seguir:
a) Embora as fórmulas dentro de um parágrafo sempre quebrem após operações e relações binárias, as fórmulas exibidas sempre quebram antes de operações e relações binárias. É por isso que não terminamos a primeira linha do nosso exemplo anterior com (2^{34} -1)+; Terminamos com (2^{34} -1 e começamos a segunda linha com+.
b) Quando uma equação é quebrada antes de uma operação binária, a segunda linha deve iniciar pelo menos dois quads à direita de onde a subformula mais interna que contém essa operação binária começa na primeira linha. Por exemplo, se você deseja quebrar
1$$\sum_{0<k<n}\left(<formula_1>+<formula_2>\right)$$No sinal de mais entre <Fórmula_1> e <Formula_2>, é quase obrigatório que o sinal de mais na segunda linha pareça um pouco à direita do parêntese esquerdo grande que corresponde a \esquerda (.
No exemplo apenas considerado, é necessário cuidar especial para dividir a fórmula em duas linhas, porque os delimitadores \left e \right não podem ser usados isoladamente: você não pode ter apenas\deixado em uma linha de uma fórmula e apenas\direita no segundo. Além disso, você deseja que os dois delimitadores tenham o mesmo tamanho, mesmo que ocorram em linhas diferentes. A melhor solução é geralmente escolher o tamanho do delimitador; Por exemplo, você pode digitar
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sum_{0<k<n}\biggl(&<formula_1>\\
6 &\qquad+<formula_2>\biggr)
7\end{align*}Se \bigg delimitadores forem melhores. Observe que os marcadores e não ocorrem em = sinais neste exemplo, eles apenas marcam um ponto de alinhamento.
Há outra maneira de quebrar fórmulas longas, às vezes chamadas de formulário de duas linhas. A idéia é colocar a primeira parte da fórmula quase nivelada à esquerda e colocar a segunda parte quase nivelada, onde “quase nivelado” significa “um quadrilátero”. Assim, a forma de duas linhas de uma longa equação sigma considerada anteriormente é
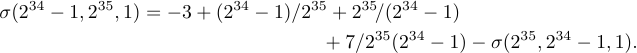
Para obter esse efeito de duas linhas, apenas digite:
1$$\displaylines{\quad\sigma(2^{34}-1,2^{35},1)
2 =-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1)\hfill{}\cr
3\hfill{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).\quad\cr}$$Um {}} extra foi digitado na segunda linha aqui, para que o Tex soubesse que o+é uma operação binária. O formulário de duas linhas é especialmente recomendado para equações que têm um lado longo esquerdo; Nesse caso, o intervalo geralmente ocorre logo antes do = sinal.