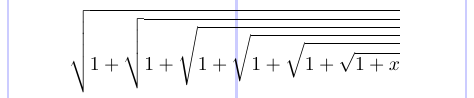5. Símbolos extensíveis e ajustáveis

No LATEX, existem certos recursos que permitem a produção de estruturas que podem crescer para qualquer tamanho necessário. A tipóstica matemática precisa extremamente de tal variabilidade. Discutiremos alguns aspectos deste artigo. Todos os comandos abordados nesta seção (a menos que indicado de outra forma) são fornecidos pelo LATEX padrão.

5.1. Elipsis …

O pacote amsmath substitui (em quase todos os casos) todos aqueles\ldots, cdots etc. do LaTex padrão com o comando \Dots. Tanto a posição vertical da elipse quanto o espaço ao redor são selecionados automaticamente, dependendo do tipo de símbolo seguindo \Dots. Se o próximo símbolo for, digamos, um sinal de plus, os pontos sairão centralizados; Se for uma vírgula, eles cairão na linha de base. São sempre três pontos, mas o espaçamento é variável.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
A series $H_1, H_2, \dots, H_n$, a sum
$H_1 + H_2 + \dots + H_n$, an orthogonal product
$H_1 \times H_2 \times \dots \times H_n$.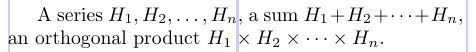

No entanto, quando os pontos aparecerem no final de uma fórmula, o próximo objeto será algo como \end ou\)ou$, e isso não dá idéia sobre o posicionamento dos pontos. Nesse caso, você deve ajudar usando \dotsc para pontos seguidos por vírgulas, \Dotsb para pontos seguidos por *operador binário *ou *símbolo de relação *, \dotsm para pontos seguidos por pontos de multiplicação,\dotsi para que outros.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
A series $H_1, H_2, \dotsc\,$, a sum
$H_1 + H_2 + \dotsb\,$, an orthogonal product
$H_1 \times H_2 \times \dotsm\,$, and an infinite
integral: \[ \int_{H_1} \int_{H_2} \dotsi \;
{-\Gamma}\, d\Theta \]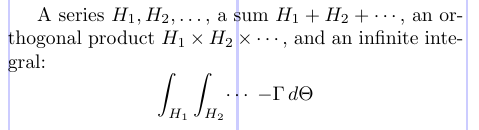

5.2. Símbolos que são horizontalmente extensíveis

Basicamente, o LATEX permite a configuração de qualquer comando de acento matemático para produzir o glifo apropriado a partir de uma variedade de larguras sempre que forem fornecidas pelas fontes disponíveis. No entanto, no LATEX padrão, existem apenas dois desses comandos: \widehat e \ widetilde.

No próximo exemplo, demonstramos o uso de alguns comandos que produzem construções semelhantes aos detalhes extensíveis acima mencionados. Todos eles produzem símbolos compostos da classe de matemática *Ordinary *.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
\widehat {\psi_\delta(t) E_t h}
&= \widetilde {\psi_\delta(t) E_t h} \\
\overline {\psi_\delta(t) E_t h}
&= \underline {\psi_\delta(t) E_t h} \\
\overbrace {\psi_\delta(t) E_t h}
&= \underbrace {\psi_\delta(t) E_t h}
& & \text{Do not change style} \\
\overrightarrow {\psi_\delta(t) E_t h} 
&= \overleftarrow {\psi_\delta(t) E_t h}
& & \text{Do not change style} \\[-3pt]
& & & \text{without \textsf{amsmath}} \\
\underrightarrow {\psi_\delta(t) E_t h}
&= \underleftarrow {\psi_\delta(t) E_t h}
& & \text{Do need \textsf{amsmath}} \\
\overleftrightarrow {\psi_\delta(t) E_t h}
&=\underleftrightarrow{\psi_\delta(t) E_t h}
& & \text{Do need \textsf{amsmath}}
\end{align*}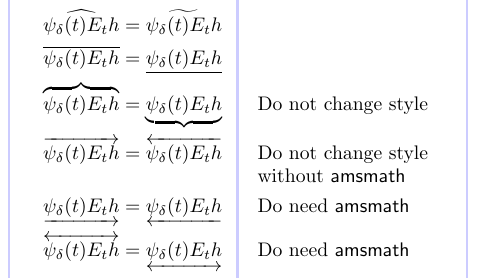

Aqui, “Change Style” significa que o símbolo empregado é afetado pelo estilo matemático em uso, para que pareça correto quando usado, por exemplo, em frações ou subscrito/superscript. Aqueles que não mudam de estilo serão lançados apenas no nível superior das fórmulas exibidas.

5.3. Símbolos que são verticalmente extensíveis

A extensibilidade vertical é muito mais larga. A tabela a seguir lista todos os símbolos que são verticalmente extensíveis.

Símbolos verticalmente extensíveis

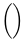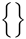	( )		\{ \}		\lVert \rVert
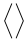	\langle \rangle		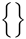\lbrace \rbrace		\lvert \rvert
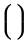	\lgroup \rgroup		[ ]		`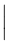
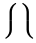	\lmoustache \rmoustache		\lbrack \rbrack		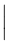\vert
	\Downarrow		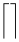\lceil \rceil		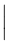\arrowvert
	\Uparrow		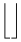\lfloor \rfloor		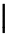\bracevert
	\Updownarrow		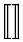\llbracket \rrbracket		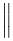\Arrowvert
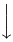	\downarrow		/		|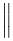
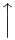	\uparrow		\backslash		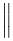\Vert
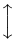	\updownarrow		.		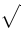\sqrtsign

Os símbolos em itálico requerem o pacote amsmath ou, se digitados a negrito, o pacote stmaryrd. Um ponto final (.) não é um símbolo extensível, mas pode ser utilizado para produzir um delimitador “invisível”. O símbolo \sqrtsign não pode ser utilizado com \left, \right ou \middle.

Sinónimos: [ - \lbrack, [; ] - \rbrack, ]; { - \lbrace, \{; } - \rbrace, \}; | - \vert, |; || - \Vert, \|.

Esses símbolos se tornam extensíveis apenas em certos usos. Eles devem ser baseados na seguinte construção:

\left <ext-Open> <sub-formula> \right <ext-Close>

Se o LaTeX estiver a utilizar o programa eTeX, também pode utilizar estes símbolos extensíveis com \middle.

Aqui <Ext-Open> e <Ext-Close> pode ser qualquer um dos símbolos (exceto \sqrtsign) listado na tabela acima. Eles devem ser símbolos que foram configurados para serem extensíveis, conforme descrito no FntGuide. Assim, um símbolo que representa a ausência de um glifo real deve estar disponível. Aconteceu que esse símbolo, também conhecido como Delimitador *Nulo *, é o período (.). Os tamanhos dos glifos reais para digitar um símbolo extensível são escolhidos para se encaixar na altura e profundidade da subformula que está entre eles.

O símbolo radical \sqrtsign cresce vertical e horizontalmente para se ajustar ao tamanho de seu argumento. No LATEX, você prefere usar o comando \sqrt para obter este símbolo.

\[
  \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 +
    \sqrtsign{1 + \sqrtsign{1 + \sqrtsign{1 + x}}}}}}
\]