8. Fórmulas matemáticas de ajuste fino
Já discutimos a maioria das instalações necessárias para construir fórmulas de matemática. Mas ainda existem alguns pontos finos que permitem produzir fórmulas realmente bonitas, as fórmulas que melhorarão a aparência geral e a legibilidade dos livros e papéis que você digitaria.
8.1. Pontuação
A regra geral é: quando uma fórmula é seguida por um período, vírgula, semicolon, cólon, ponto de interrogação, ponto de exclamação, etc., coloque a pontuação após o $, quando a fórmula estiver no texto; Mas coloque a pontuação antes do $$ quando a fórmula for exibida. Por exemplo,
1If $x<0$, we have shown that $$y=f(x).$$Então, você nunca deve digitar nada como
1for $x = a, b$, or $c$.Deve ser
1for $x = a$, $b$, $c$.No primeiro caso, o Tex tipando $ x = a, b $ como uma única fórmula, colocando um espaço fino entre a vírgula e o b. Esse espaço não será o mesmo que o espaço entre a vírgula e o C, pois os espaços entre as palavras são sempre maiores que os espaços finos. Esse espaçamento parece ruim, mas no segundo caso o espaçamento parecerá bom.
Também é importante que o Tex nunca quebre uma linha de um parágrafo no espaço entre a vírgula e o b porque quebra depois de vírgulas em fórmulas geralmente estão erradas como na equação$ x = f (x, a) $. Assim, a possibilidade de quebrar linhas em um parágrafo é inibida, o que leva a uma aparência pior do documento de Typeset. Em outras palavras, se um ponto de pontuação pertence linguisticamente à frase e não à fórmula, deixe -a fora dos $ ‘.
8.2. Cartas não Ítilas
Funções matemáticas comuns como “log” são sempre definidas no tipo romano. A melhor maneira de incluir esses objetos em uma fórmula é usar os seguintes comandos:

Nos exemplos a seguir, alguns desses comandos são usados:

As duas últimas fórmulas exibidas mostram que alguns dos comandos são tratados pelo TEX como grandes operadores com limites como o sinal de soma. E o subscrito em \max não é tratado como o subscrito em\log. Os subscritos e os superestritos se tornarão limites quando estiverem anexados a \det, \ gcd, \inf, \lim, \liminf, \limsup, \max, \min \pr e` `` sup.
Se você precisar de um tipo romano para uma função ou operador frequentemente usado que não está listado acima, poderá definir facilmente seu próprio comando. Suponha que você queira definir um operador com limites e chamá -lo de \oper. Para fazer isso, você deve incluir a seguinte definição no preâmbulo:
1\def\oper{\mathop{\rm oper}}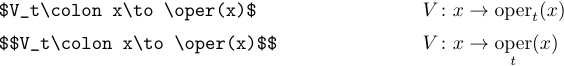
Caso seu operador não tenha limites, use uma definição como a seguinte:
1\def\oper{\mathop{\rm oper}\nolimits}Se você precisar de um tipo romano apenas para um único uso, é mais fácil mudar para \rm tipo da seguinte forma:
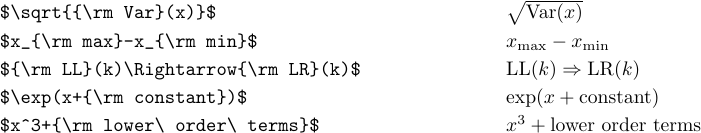
Observe os usos de ‘' no último caso. Sem eles, os espaços em branco comuns teriam sido ignorados e ‘Termos da Ordem Inferior’ teriam sido digitados como “inferiores a termos”.
A palavra “mod”, que também é geralmente definida em fórmulas romanas, precisa de mais cuidados, porque é usada de duas maneiras diferentes. O LATEX fornece o comando \bmoda ser usado quando" mod “é uma operação binária e o comando \pmoda ser usado quando “mod” ocorre entre parênteses no final de uma fórmula.

Observe que \pmod insere seus próprios parênteses; A quantidade que aparece após o “mod”, pois os parênteses devem ser incluídos no aparelho, a menos que seja um único símbolo.
Você também pode obter outros estilos do tipo da mesma maneira que obtém do tipo romano usando \rm. Por exemplo, \bf dá Boldface:

Você pode notar que o ‘+’ e ‘=’ ainda estão do tipo romano. LaTeX sets things up so that commands like \rmand \bfaffect only the uppercase letters A to Z, the lowercase letters a to z, the digits 0 to 9, the uppercase Greek letters \Gamma to \Omega, and math accents like \hatand \tilde. Aliás, nenhum aparelho foi usado neste exemplo, pois $ ’’ tem o efeito do agrupamento; \bfaltera a fonte atual, mas a alteração é local, por isso não afeta a fonte atual fora da fórmula.
Você também pode dizer \cal em fórmulas para obter letras maiúsculas em um estilo” caligráfico “.

Isto funciona apenas com as letras
AaZ; obterá resultados estranhos se aplicar\cala letras minúsculas ou gregas.
Há também \mit, que significa” Math Italic “. Isso afeta o grego em maiúsculas.
Quando \mit está em vigor, as letras comunsa para z ea para z não são alteradas; Eles são definidos em itálico como de costume, porque normalmente vêm da fonte Italic Math. Por outro lado, cartas gregas e detalhes em matemática não são afetados por \rm, já que eles normalmente vêm da fonte romana.
Com o LATEX, você também pode digitar \it ou \ tt para obter letras de itálico ou máquina de escrever em sua fórmula. Você provavelmente se pergunta por que `` mite\itsão fornecidos. A resposta é que\mité" Math Italic "(que geralmente é melhor para fórmulas), e\It ‘é “texto itálico” (o que geralmente é melhor para o texto em execução).
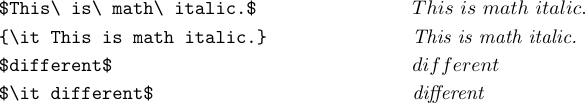
As letras em itálico de matemática são mais amplas e o espaçamento é diferente. Isso funciona melhor na maioria das fórmulas, mas a aparência sofre quando você tenta digitar certas palavras em itálico como “diferente” no modo de matemática. Um amplo ‘f’ em itálico é geralmente desejável em fórmulas, mas não em texto. Portanto, é melhor usar \it em uma fórmula que deveria conter uma palavra em itálico real. Geralmente, este não é um caso de matemática clássica, mas é um caso comum quando os programas de computador estão sendo digitados:

O segundo exemplo mostra o uso de sublinhados curtos para dividir nomes de identificadores.
8.3. Espaçamento entre fórmulas
É um caso comum quando uma tela contém mais de uma fórmula; Por exemplo, uma equação pode ser acompanhada por uma condição lateral:
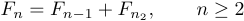
Nesses casos, você precisa dizer a Tex quanto espaço para colocar depois da vírgula, porque as convenções normais agrupariam as coisas. Para conseguir isso, você pode digitar
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.Aqui, \qquad significa” Double Quad “, onde” Quad “significa alguma quantidade de espaço comum para impressoras. Assim \quad significa quad -espaço de uma impressora na direção horizontal. Sempre que você quiser espaçamento, difere das convenções normais, você deve especificá -lo explicitamente usando comandos como \quad e \qquad.
Um quadra costumava ser um pedaço quadrado do tipo em branco, 1 de largura e 1em de altura - aproximadamente do tamanho de um capital m; Mas o Quad do LATEX não tem altura.
No texto de um parágrafo, as fórmulas parecem melhores se forem separadas por palavras, não apenas por vírgulas. Mas se realmente não houver texto para inserir, você deve pelo menos colocar algum espaço entre as fórmulas. Comparar
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.e
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.que dão
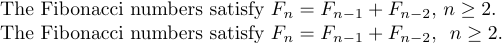
O ‘' aqui dá uma separação visual que compensa parcialmente o estilo ruim.
8.4. Espaçamento nas fórmulas
Já vimos que o Tex faz espaçamento automático de fórmulas de matemática, o que as faz parecer certas na maioria dos casos. No entanto, é natural que as exceções surjam, uma vez que o número de fórmulas possíveis é enorme e as regras de espaçamento da Tex são bastante simples. Portanto, é desejável ter unidades finas de espaçamento para tais casos, em vez das peças grandes que surgem de \, \quad e \qquad.
Os elementos básicos do espaço que Tex coloca em fórmulas são chamados de espaços finos, espaços médios e espaços grossos. A Tex os insere automaticamente em fórmulas, mas você pode adicionar seu próprio espaçamento sempre que quiser, usando os comandos

As fórmulas que envolvem cálculo parecem melhores quando um espaço extra fino é inserido antes dx ou dy ou d qualquer coisa; Mas Tex não faz isso automaticamente. Os exemplos a seguir mostram como contar a Tex sobre essas necessidades:

Observe que nenhum \, foi necessário após o / na segunda última fórmula. Também não há necessidade de \, no último exemplo, pois o dt aparece por si só no numerador de uma fração; Isso o destaca visualmente do restante da fórmula.
As unidades físicas, quando aparecem em uma fórmula, devem ser definidas no tipo romano e separadas do material anterior por um espaço fino:

Espaços finos também devem ser inseridos após os pontos de exclamação (operação fatorial), se o próximo personagem for uma carta ou um dígito ou um delimitador de abertura:
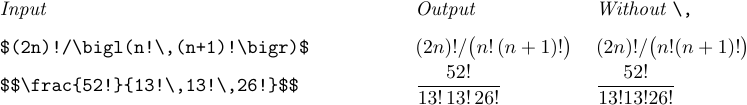
Além desses casos, você ocasionalmente encontra fórmulas nas quais os símbolos são agrupados com muita força, ou onde o muito espaço em branco aparece, por causa de certas combinações de formas infelizes. Um aplicado com bom gosto \, ou \! abrirá as coisas ou fechará as coisas juntas para que o leitor não seja distraído do significado matemático da fórmula. Radicais e múltiplas integrais geralmente são candidatos a um ajuste fino. Aqui estão alguns exemplos de situações a serem observadas:

As regras de espaçamento do Tex às vezes falham quando ‘|’ e ‘\ |’ aparecem em uma fórmula, porque esses símbolos são tratados como símbolos comuns em vez de delimitadores. Considere as fórmulas
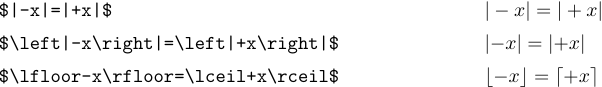
No primeiro caso, o espaçamento está errado porque Tex acha que o sinal de mais está calculando a soma de | e ‘x’. O uso de \left e \right no segundo exemplo coloca o Tex na pista direita. O terceiro exemplo mostra que essas correções não são necessárias com outros delimitadores, porque a Tex sabe se são aberturas ou fechamentos.
8.5. Elipses
Uma elipse pode ser indicada por dois tipos diferentes de pontos, um maior que o outro. As melhores tradições distinguem entre essas duas possibilidades. Geralmente é correto produzir fórmulas como
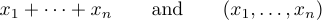
mas errado em produzir fórmulas como
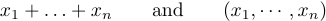
A idéia é digitar \ldots quando você deseja três pontos baixos e \cdots quando você deseja três pontos verticalmente centrados. Em geral, é melhor usar \cdots entre + e - e sinais de multiplicação, e também entre=sinais ou” letreiros menos do que ou equals “ou sinais de subconjunto ou outras relações semelhantes. Pontos baixos são usados entre vírgulas e, quando as coisas são justapostas, sem sinais entre eles:
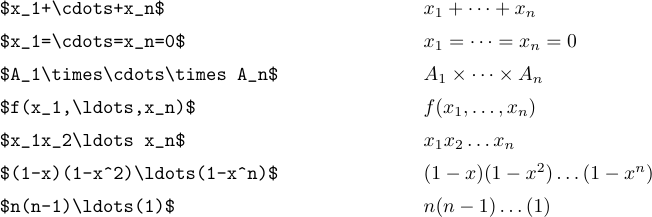
Mas há um caso especial em que \ldots e \cdots não produzem o espaçamento certo. Isso acontece quando eles aparecem no final de uma fórmula ou pouco antes de um delimitador final. Em tais situações, é necessário um espaço extra fino. Por exemplo, considere as seguintes frases:
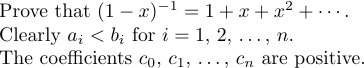
A primeira frase é produzida digitando
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.Sem o \, o período teria chegado muito perto do \cdots.
A segunda frase foi digitada como:
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.Observe o uso de laços (~), que evitam quebras de linha ruim. Tais elipses são muito comuns em algumas formas de escrita matemática, então o LATEX fornece a macro \dots como uma abreviação para$ \ ldots \, $para usar no texto de um parágrafo. A terceira frase pode, portanto, ser digitada
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6. Quebra de linha
Quando você tem fórmulas em um parágrafo, o TEX pode ter que quebrá -las entre as linhas. Ele quebrará uma fórmula somente após um símbolo de relação, ou após um símbolo de operação binária, onde a relação ou operação binária está no nível externo da fórmula, o que significa que não é incluído em {...}. Por exemplo, se você digitar
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$No meio do parágrafo, há uma chance de Tex quebrar após um dos sinais = preferidos) ou após o - ou + ou - (em uma emergência). Mas não haverá uma pausa após a vírgula, em qualquer caso, já que vírgulas após as quais os intervalos são desejáveis não devem aparecer entre $ ‘’.
Você não quer permitir quebrar neste exemplo, exceto após os sinais = você pode digitar
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$Porque esses aparelhos adicionais “congelam” as subformulas, colocando -as em caixas inquebráveis. Mas não há necessidade de se preocupar com essas coisas, a menos que Tex realmente quebre uma fórmula, pois a possibilidade disso é bastante baixa.
Se você deseja permitir a quebra em algum momento do nível externo de uma fórmula, pode dizer \allowbreak. Por exemplo, se a fórmula
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$Aparece no texto de um parágrafo, Tex permitirá que ele seja dividido em dois pedaços
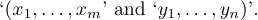
8.7. Aparelho ortodôntico
Os símbolos ‘{’ e ‘}’ são usados em várias notações diferentes, e o LATEX fornece alguns comandos para ajudá -lo a lidar com fórmulas que envolvem essas coisas. O caso mais simples é quando os aparelhos são usados para indicar um conjunto de elementos. Por exemplo, “{a, b, c}” significa o conjunto de três elementosa, b e c:
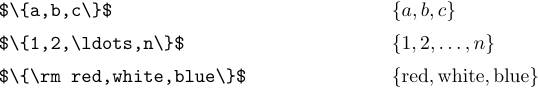
Um conjunto também pode ser indicado fornecendo um elemento genérico seguido por uma condição específica. Por exemplo, o conjunto de todos os objetos x maiores que 5 pode ser escrito da seguinte maneira:

Estas são duas variantes para indicar o mesmo conjunto. O primeiro exige o uso de \mid para obter a barra vertical, enquanto a segunda não requer nada, exceto o cólon, que é tratado como uma operação binária.
Quando os delimitadores ficam maiores, eles devem ser chamados de \bigl, \bigm e \bigr:
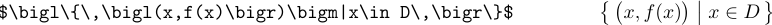
As fórmulas com delimitadores ainda maiores usariam \big ou\bigg ou até \bigg comandos.
Você também pode encontrar outro uso de aparelhos nas fórmulas exibidas. Na verdade, é uma chave esquerda que indica uma escolha entre várias alternativas:
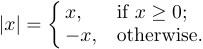
Esta construção pode ser digitada usando o comando \case:
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$Cada um dos casos possui duas partes separadas pelo símbolo &, que desempenha um papel especial na construção de estruturas tabulares. À esquerda do & é uma fórmula de matemática implicitamente fechada em $ ... $; À direita do & é texto comum. Portanto, -x, na segunda linha, estará digitando no modo matemático, mas o caso contrário será compensado no modo horizontal. Os espaços em branco antes e depois dos & são ignorados. Pode haver vários casos, embora geralmente haja apenas dois. Cada caso deve ser seguido por \cr.
Os aparelhos horizontais serão definidos sobre ou sob partes de uma fórmula exibida se você usar os comandos \overbrace ou \ Underbrace. Tais coisas são consideradas operadoras grandes como \sum, para que você possa colocar limites acima ou abaixo deles especificando superestritos ou subscritos:

8.8. Matrizes
Matrizes são objetos bastante comuns nas fórmulas matemáticas; São apenas matrizes retangulares de fórmulas que são dispostas em linhas e colunas. O LATEX fornece o comando \matrix para lidar com os tipos mais comuns de matrizes.
Por exemplo, suponha que você queira especificar a tela
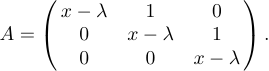
Tudo que você faz é digitar
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$Isso é bastante semelhante à construção \casos que analisamos anteriormente; Cada linha da matriz é seguida por \cr eb &sinais são usados entre as entradas individuais de cada linha. No entanto, ao contrário de \casos, você deve colocar seus próprios delimitadores\left e \right” em torno da matriz. O motivo é que diferentes delimitadores podem ser usados em diferentes construções de matriz. Por outro lado, os parênteses são usados com mais frequência do que outros delimitadores, para que você possa digitar \pmatrix se deseja que o Latex defina os parênteses para você:
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$Cada entrada de uma matriz é normalmente centrada em sua coluna e cada coluna se expande o máximo necessário para acomodar as entradas que ela contém, e há um quadrilátero entre as colunas. Se você quiser que algo saia para a esquerda/direita em sua coluna, siga/precede -a por \hfill.
Cada entrada de uma matriz é processada separadamente dos outros e é compensada como uma fórmula matemática no estilo de texto. Assim, por exemplo, se você disser \rm em uma entrada, ela não afeta os outros. Dizendo {\ rm x & y} é inválido.
As matrizes geralmente aparecem como padrões genéricos que usam elipses para indicar linhas ou colunas que são deixadas de fora. Você pode compensar essas matrizes colocando as elipses em suas próprias linhas e/ou colunas. Além de \ldots, o LATEX fornece \vdots (pontos verticais) e \ddots (pontos diagonais) para tais construções. Considere a seguinte matriz
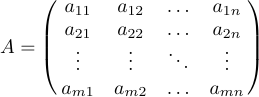
que é especificado como:
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$Às vezes, uma matriz é delimitada na parte superior e deixada por fórmulas que fornecem rótulos às linhas e colunas. Para esta situação, uma macro especial chamada \bordermatrix é definida no LaTeX. Por exemplo, a tela
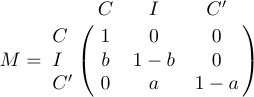
é obtido quando você digita
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$A primeira linha fornece os rótulos superiores, que aparecem acima dos parênteses grandes e direito; A primeira coluna fornece os rótulos esquerdos, que são nivelados com o tipo de nivelamento, pouco antes da própria matriz. O elemento na interseção da primeira coluna e a primeira linha está normalmente em branco. E como \pmatrix, \bordermatrix insere seus próprios parênteses.
Colocar matrizes no texto de um parágrafo geralmente é desviado. O motivo é que eles são tão grandes que são melhor exibidos. Mas ainda assim, você pode ocasionalmente querer negligenciar isso. Nesse caso, você pode usar \escolha ou\no top:
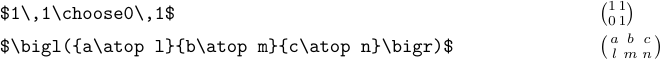
A macro \matrix não produz pequenas matrizes como essa.