7. Presça os ajustes no layout

Geralmente, o LaTeX faz um ótimo trabalho ao estabelecer fórmulas de matemática. Mas, às vezes, é necessário um ajuste mais fino do posicionamento. Este artigo discute algumas técnicas para ajustar o layout para melhorar as fórmulas de matemática.

7.1. Dimensionamento e espaçamento automáticos

Os símbolos e letras matemáticos geralmente ficam menores (e com espaçamento mais apertado), quando aparecem em frações, subscritos ou superscritos. As fórmulas de matemática podem ser dispostas em oito estilos de matemática Tex:


D, D'	`\displaystyle`	Exibidos em linhas por si só
T, T'	`\textstyle`	Incorporados no texto
S, S'	`\scriptstyle`	Em sobrescritos ou subscritos
SS, SS'	`\scriptscriptstyle`	Em todos os sobrescritos ou subscritos de ordem superior

O estilo de texto (T) é utilizado no nível superior de uma fórmula definida em texto corrido (entre um par de $ ou entre $ e $), enquanto o estilo de apresentação é utilizado no nível superior de uma fórmula apresentada (entre um par de $$ ou entre \[ e \]). Quanto às subfórmulas, o estilo pode ser determinado a partir da seguinte tabela:


D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

O próximo exemplo ilustra os vários estilos:

 1\normalsize                 %% Style:
 2\[ b                        %% D
 3    ^0                      %% S
 4   +                        %% D
 5   \frac{(k + p)            %% T
 6          _{j'}             %% S'
 7         % \displaystyle
 8         \pm                %% T [D]
 9         \frac{(f + q)      %% S [T]
10                ^{(pk)      %% SS [S]
11                   ^y       %% SS
12                   _{j'}}}  %% SS'
13              {(h + y)}}    %% S' [T']
14        {(l + q)            %% T'
15          ^{(pk)}}          %% S'
16\]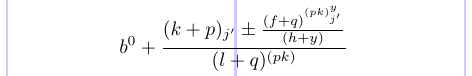

$Vários estilos de matemática$

Você pode remover o char de comentário (%) antes de \displaystyle e ver como alguns dos estilos mudaram para os colchetes:

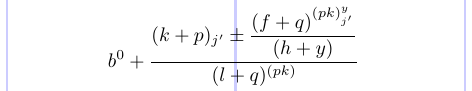
$Estilos de matemática explicitamente mudados$

Ele mostra como especificar explicitamente o estilo a ser usado em cada parte.

7.2. Submormulas

No texto, um par de aparelhos indica um grupo, ou um escopo, dentro do qual alguma declaração está em vigor. Dentro de uma fórmula de matemática, eles, além disso, delimitam uma sub-formula, que é sempre digitada como uma entidade separada que é adicionada à fórmula externa. Como conseqüência, as submormulas são sempre digitadas em sua largura natural e não se estendem ou encolhem horizontalmente quando a Tex constrói um parágrafo tentando encaixar a fórmula em uma linha. Já mostramos que a submormula de um grupo simples é processada como se fosse um único símbolo. Isso significa que um grupo vazio produz um símbolo invisível que pode alterar o espaçamento.

O conteúdo dos subscritos/superestritos e os argumentos de muitos (mas não todos) comandos, como \frac e \mathrel, também são sub-formulas. Assim, eles recebem o mesmo tratamento especial. O argumento de \bm, por exemplo, não é necessariamente definido como uma sub-formula, e essa é uma das exceções importantes. Em uma fórmula de matemática, se você precisar limitar apenas o escopo de uma declaração, defina um grupo usando \borbingroup e \endGroup. Lembre-se de que declarações matemáticas especializadas, como mudanças de estilo, aplicam-se até o final da subestima atual, independentemente de outros grupos estarem ou não presentes.

7.3. Grandes delimitadores

O LATEX define quatro comandos - \big, \big, \bigg e bigg - para fornecer controle direto dos tamanhos de delimitadores extensíveis. Eles pegam um único argumento, que deve ser um delimitador extensível, e produzir versões maiores do delimitador, de 1,2 a 3 vezes o tamanho da base.

Existem também três variantes para cada um dos quatro comandos, dando quatro tamanhos de símbolo de abertura (\bigl, \bigl, \biggl e \biggl); quatro tamanhos de * símbolo de relação * (\bigm, \bigm, \biggm e \biggm); e quatro tamanhos de símbolo de fechamento (\bigr, \bigr, \biggr e \biggr). Todos esses 16 comandos devem ser usados com qualquer símbolo que possa vir depois de \esquerd ', \ Right, ou (com Etex) \middle` (veja esta tabela).

Os tamanhos desses delimitadores são fixados no LaTeX padrão. No entanto, com o pacote amsmath, os tamanhos se adaptam ao tamanho do material circundante, de acordo com o tamanho da fonte e o estilo de matemática em uso. Isso é mostrado no exemplo abaixo.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]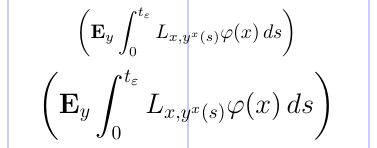

$Delimitadores adaptando -se ao tamanho atual da fonte e ao estilo de matemática$

7.4. Ajustando o índice em um radical

A colocação do índice em um sinal radical nem sempre é bom no LaTeX padrão. No entanto, você pode usar os comandos \leftroot e \uproot definidos no pacote amsmath para ajustar o posicionamento desse índice. Argumentos inteiros positivos para esses comandos movem o índice para a esquerda e para cima, respectivamente, enquanto argumentos negativos o movem para a direita e para baixo. Esses argumentos são apresentados em unidades de matemática, que são bem pequenas, portanto, esses comandos são adequados para ajuste fino.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4  \sqrt[\beta]{k} \qquad
5  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]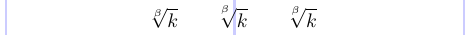

$Ajustando o índice de um sinal radical$

7.5. Ajuste fino com suportes e fantasmas

Sempre que você deseja “perfeitamente” o espaçamento e o alinhamento de matemática, geralmente é melhor recorrer a habilidades únicas e avançadas do Primitivo Tex. O acesso a esses recursos é fornecido por vários comandos relacionados a \phantom e \smash. Esses comandos podem ser usados em fórmulas matemáticas ou em texto em execução.

Vamos dar uma olhada no exemplo a seguir:

 1\usepackage{amsmath}
 2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
 3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
 4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
 5\newcommand\bfE{\mathbf{E}}
 6% -------------------------------------------------------------------------------
 7\begin{equation} \begin{split}
 8  f_{h, \ve}(x, y)
 9    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
10    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
11    &\relphantom{=} {} + h \biggl[
12       \frac{1}{\tve}
13       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
14               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
15    &\relphantom{=} \phantom{{} + h \biggl[ }
16       \frac{1}{\tve}
17       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
18               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19                                            \vf(x) \,ds    \biggr) \biggr]
20\end{split} \end{equation}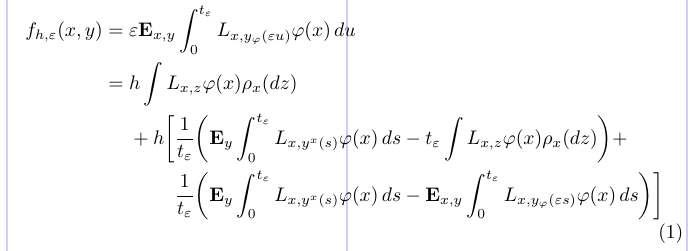

$Os fantasmas da fórmula$

Aqui, o comando \phantom recebe o posicionamento horizontal ajustado. No preâmbulo, é usado para definir um símbolo de relação invisível igual em largura ao seu argumento (= neste exemplo). Dentro dos ambientes de matemática, ele é usado para alinhar certas linhas iniciando-as com um “fantasma”, ou invisível, sub-formula. O par vazio de aparelhos {} é o mesmo que \mathord {}, que produz um símbolo invisível de largura zero necessária para obter o espaçamento correto de “+ *h *” (sem {} `, o sinal de mais produzirá mais unário com um espaço inadequado antes *h *).

Ao contrário de \phantom, o comando \smash digita seu conteúdo (em uma caixa LR), mas depois ignora sua altura e largura, como se ambas fossem zero. O comando \hphantom, definido no LaTeX padrão, é uma combinação dos dois. Produz o equivalente a \smash {\ Phantom {algum conteúdo fantasma}}, isto é, uma caixa invisível com altura e profundidade zero, mas a largura do conteúdo fantasma.

O comando \vphantom é semelhante, mas torna a largura do fantasma zero preservando sua altura total mais profundidade. O comando \mathStrut é definido como \vphantom (e produz uma caixa de altura e profundidade de largura zero igual à de um parêntese.

Com o pacote amsmath, o comando \smash pode assumir um argumento opcional, de modo que \smash [t] {...} ignora a altura do conteúdo da caixa, mantendo a profundidade, enquanto \smash [b] {...} ignora a profundidade, mantendo a altura.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

$Esmagando a expressão radical$

Parece que dar a y alguma altura extra com um suporte fará com que os radicais pareçam semelhantes. Mas, em vez disso, isso os faz parecer mais diferentes e mais feios no todo. Acontece que esmagar o fundo do y é a melhor maneira.

O exemplo a seguir mostra um uso muito comum de esmagar. O comando \smash é usado lá para fornecer um bom controle sobre a altura dos delimitadores circundantes. Também mostra que o esmagamento pode causar problemas, pois a altura real da linha precisa ser conhecida. Isso é reparado por \vphantom. \hmjd é o símbolo composto definido como:

1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Para mostrar o espaço vertical resultante, adicionamos regras:

Aparência	`Código`	Comentário
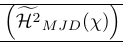$“Parêntesis externos demasiado grandes”$	`\left( {\Hmjd } \right)`	Parênteses exteriores muito grandes
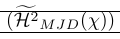$“Parênteses externos demasiado pequenos e regras demasiado próximas”$	`\left( \smash{\Hmjd } \right)`	Parênteses exteriores muito pequenos e regras muito próximas
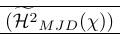$“Perfeitamente correcto”$	`\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}`	Exatamente!
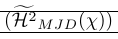$“Vphantom e Smash Parcial Necessários”$	`\left( \smash[t]{\Hmjd } \right)`	Tanto `\vphantom` como Smash Parcial são necessários

Em alguns casos, deficiências no processamento TeX de baixo nível podem levar a erros nos detalhes da composição. Isto pode ocorrer em layouts específicos em que (a) uma subfórmula (numerador/denominador de uma fracção ou subscrito/sobrescrito) consiste exactamente numa caixa LR, ou numa caixa matemática construída de forma semelhante, e também (b) esta caixa não tem o seu tamanho natural, como nas formas mais complexas de \makebox, smashes e alguns fantasmas.

Para ver isso, vejamos o seguinte exemplo:

1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]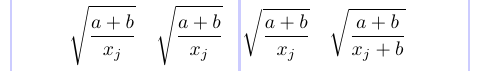

$Problemas causados por esmagadores$

Para reduzir a profundidade do radical, um \smash foi adicionado no segundo radical, mas isso não teve efeito. No terceiro radical, trabalhou com um grupo vazio. Mas, no quarto radical, nenhum grupo vazio era necessário. Para resumir, sempre que você encontrar o \smash não funciona, tente adicionar uma sub-formula de matemática vazia ({}) antes da caixa solitária, para tratá-la corretamente.

7.6. Espaçamento horizontal

A ajuste mais fina e mais difícil requer os comandos de espaçamento explícitos mostrados na tabela a seguir:

$Comandos de espaçamento horizontal$

As formas completas e curtas desses comandos são robustas e também podem ser usadas fora das fórmulas matemáticas no texto normal. Eles estão relacionados a espaços finos, médios e grossos disponíveis nas máquinas usadas para matemática digita em meados do século XX.

Os valores atuais dos três parâmetros tex \thinMuskip, \medMuskip e \dephshmuskip definem a quantidade de espaço adicionada por esses comandos \ .. espacial. Seus valores padrão com amsmath estão listados na tabela. Esses parâmetros de baixo nível requerem valores nas unidades de matemática (mu). Portanto, eles só podem ser definidos por meio de atribuições Tex de baixo nível, não por \setLength ou similar. Além disso, normalmente seus valores não devem ser modificados, pois são usados internamente pela matemática da Tex (consulte a tabela a seguir).

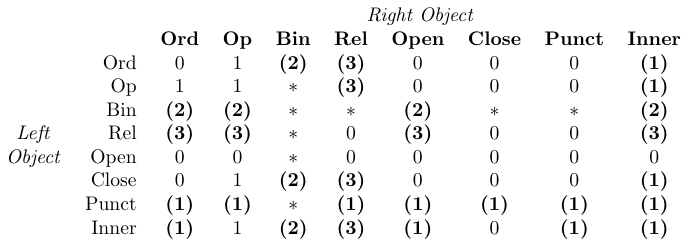
$Espaçamento entre símbolos$

Na tabela, 0 significa “sem espaço”, 1 significa \thinmuspace, 2 significa \medmuskip, 3 significa \thickmuskip e significa “impossível”. As entradas a negrito significam que o espaçamento correspondente não é adicionado nos estilos de escrita matemática.

Uma unidade de matemática (1MU) é igual a 1/18 de um em no tamanho atual da fonte de matemática. Segue -se que o valor absoluto de A * mu varia com um estilo de matemática, dando espaçamento consistente, independentemente do estilo usado.

Texto em fórmulas de matemática Fontes de matemática de LaTeX