8. Fontes em fórmulas matemáticas

Introdução às fontes de LaTeX

Ao contrário do texto flutuante, você geralmente não precisaria de alterações automáticas nas formas de fonte. Formas diferentes têm significados específicos em matemática. Por exemplo, letras verticais em negrito podem ser usadas para vetores. Se os caracteres de uma fórmula mudassem devido às condições circundantes, o resultado estaria incorreto. É por isso que o manuseio de fontes nas fórmulas matemáticas difere daquela no texto.

Os caracteres de uma fórmula podem ser divididos em duas classes: símbolos e caracteres alfabetistas (incluindo dígitos). Na verdade, o Tex lida internamente com oito classes que definem o espaçamento apropriado. Mas para a discussão atual, a divisão em duas classes é suficiente.

Alguns símbolos, como =, podem ser inseridos diretamente no teclado. No entanto, parte deles deve ser inserida por meio de um comando, por exemplo, \leq fornece um sinal menor ou igual. O outro grupo principal de caracteres de uma fórmula, os caracteres do alfabeto, são inseridos diretamente no teclado.

Existem mais de 200 símbolos predefinidos no LaTeX padrão. Ele permite que o usuário digita quase qualquer fórmula desejada. Esses símbolos estão localizados em várias fontes diferentes, mas podem ser acessados ​​de tal maneira que o usuário não precisa estar ciente de como eles são representados internamente. Se necessário, fontes de símbolo adicionais podem ser acessíveis de maneira semelhante.

Símbolos e caracteres do alfabeto têm uma diferença mais importante para nós agora: os símbolos têm a mesma representação gráfica em uma fórmula, enquanto o usuário pode alterar a aparência dos caracteres do alfabeto. Os comandos que alteram a aparência dos caracteres do alfabeto em uma fórmula são chamados de identificadores de alfabetos matemáticos *, e as fontes associadas a esses comandos são chamadas de alfabetos matemáticos. Uma fórmula não muda se for colocada, digamos, dentro de um ambiente de teorema em que o texto é digitado em itálico por padrão, porque os identificadores do alfabeto são independentes dos comandos de fontes circundantes fora da fórmula. Esse comportamento é muito importante porque as formas de caráter carregam significados que devem permanecer inalterados onde quer que a fórmula apareça em um documento.

8.1. Identificadores de alfabetos matemáticos

Um alfabeto e um grande número de símbolos não são suficientes para os cientistas. Eles tentam usar todos os tipos de letra disponíveis para denotar conceitos especiais. Além de alfabetos estrangeiros, como letras gregas, que geralmente são acessadas como símbolos - \alpha, \beta, etc. - Podemos encontrar letras com serifa para matrizes, cartas serift em negrito para vetores, Fraktur Fonts para grupos, ideais ou campos. Outros usam formas caligráficas para denotar conjuntos. O número de convenções é infinito e diferem de uma disciplina para outra. E o LaTeX acomoda isso, possibilitando que os identificadores de alfabetismo de novos matemáticos e associá -los a qualquer grupo de forma de fonte desejado, em vez de confiar apenas em um conjunto predefinido que não pode ser estendido. Esses identificadores são comandos especiais para uso em uma fórmula que digita qualquer caractere alfabeto em seu argumento em um tipo de letra específico. Esses identificadores podem usar diferentes tipos de letra em diferentes fórmulas, como veremos mais tarde, mas dentro de uma fórmula, eles sempre selecionam o mesmo tipo de letra, independentemente das condições circundantes.

Identificadores de alfabeto predefinidos

O LATEX já possui alguns identificadores de alfabeto embutidos. Eles são mostrados na tabela abaixo. As duas últimas linhas mostram que as letras usadas nas fórmulas são retiradas do alfabeto de matemática \mathNormal. Por outro lado, as cartas produzidas por \mathit têm espaçamento diferente, o que significa que esse alfabeto pode ser usado para fornecer nomes de variáveis ​​de palavras inteiras comuns em algumas disciplinas.

Command	Example code	Result
\mathcal	$\mathcal{A}=a$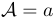
\mathrm	$\mathrm{max}_i$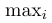
\mathbf	$\sum x = \mathbf{v}$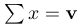
\mathsf	$\mathsf{G}_1^2$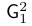
\mathtt	$\mathtt{W}(a)$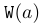
\mathnormal	$\mathnormal{abc}=abc$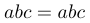
\mathit	$differ\neq\mathit{differ}$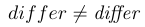

No LATEX2E, os identificadores do alfabeto matemático são comandos com um argumento, uma única letra ou uma única palavra a ser digitada em uma fonte especial.

Therefore, $\mathsf{G}$ can be computed as
\begin{equation}
\mathsf{G} = \mathcal{A} +
             \sum_{i=1}^{n} \mathcal{B}_{i}
\end{equation}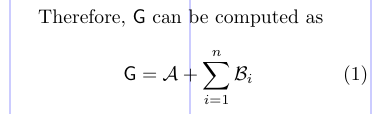

*** Alfabeto de matemática padrão***

Se você não especificar um identificador de alfabeto explicitamente, de qual alfabeto os caracteres do alfabeto são selecionados? Em outras palavras, qual é o alfabeto matemático padrão? A resposta é que não existe um único alfabeto matemático padrão. O sistema LATEX pode ser configurado para que caracteres alfabéticos sejam buscados de diferentes alfabetos, a menos que o usuário peça explicitamente um específico, e esse é normalmente o caso, como mostra o exemplo a seguir.

\begin{eqnarray}
x &=& 12345 \\
\mathrm{x} &=& \mathrm{12345} \\
\mathnormal{x} &=& \mathnormal{12345}
\end{eqnarray}

Aqui você pode ver que \mathrm não altera os dígitos e \mathnormal não altera as letras; portanto, o padrão para dígitos na configuração normal é o alfabeto matemático associado a \mathrm e o padrão para as letras é o associado a \mathnormal. Esse comportamento pode ser controlado com o comando \declaremathSymbol.

Que fonte o LaTeX usa para matemática?

No LATEX, a fonte padrão usada para o modo de matemática é tipicamente *computador moderno *. No entanto, você também pode usar fontes diferentes, especificando -as no seu preâmbulo do documento de LaTeX usando pacotes.

Identificadores de alfabeto personalizados

Você pode usar o comando \declaraMathalphabet para definir um novo identificador de alfabetos matemáticos. Digamos que você deseja disponibilizar um tipo de letra sem serifa sem serifa como um alfabeto de matemática. Primeiro, você decide sobre um novo nome de comando, como \msfsl, a ser usado como o identificador de alfabetos. Em seguida, você se refere à tabela de classificação da fonte abaixo para encontrar um grupo de forma de fonte adequado para atribuir a este identificador de alfabetismo.

Você descobrirá que a família SANS do computador, por exemplo, consiste em uma série média com formas verticais e inclinadas. Se você decidir usar a forma inclinada dessa família, informa ao LATEX usando \decloneemathalphabet.

\DeclareMathAlphabet{cmd}{encoding}{family}{series}{shape}

Existem quatro parâmetros (além do próprio identificador) na declaração: o nome da codificação, a família, a série e a forma da fonte a ser usada. O identificador de alfabetos definido no exemplo a seguir sempre mudará para SANS moderno do computador média inclinada.

\DeclareMathAlphabet{\msfsl}{OT1}{cmss}{m}{sl}
% -------------------------------------------------------------------------------
We demonstrate this with the formula
\begin{equation}
\sum \msfsl{A}_{i} = a \tan \beta
\end{equation}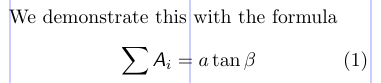

Você também pode redefinir um identificador de alfabeto de matemática existente em um arquivo de pacote ou no preâmbulo do seu documento. Por exemplo,

\DeclareMathAlphabet{\mathsf}{OT1}{pag}{m}{n}

substituirá as configurações padrão para o identificador de alfabetos \mathsf. Ele mudará para Adobe Avant Garde em suas fórmulas.

Note that if the math alphabet in question is part of a symbol font that is already loaded by LaTeX for other reasons (e.g., \mathcal), it is better to use \DeclareSymbolFontAlphabetas it makes better use of TeX’s somewhat limited resources for math.

Melhores fontes de matemática

Além de padrão FONT MODERNO DE COMPUTADOR, o LATEX oferece sete fontes embutidas para alfabetos matemáticos com tipo de composição, para que os usuários possam personalizar suas expressões de matemática sem exigir pacotes adicionais no preâmbulo. E a melhor opção para você é usar uma dessas 8 fontes.

Fonte	Utilização	Comando
Upright Roman	Fonte Upright padrão	\mathrm{}
Caligráfica	Utilizada para compor letras matemáticas comuns.	\mathnormal{}
Caligráfica	Utilizada para compor letras maiúsculas com um tipo de letra caligráfica especial.	\mathcal{}
Letras itálicas	Transformar o texto em itálico	\mathit{}
Upright Sans Serif	Define letras Sans Serif verticais	\mathsf{}
Upright Roman em negrito	Utilizada para compor letras romanas verticais em negrito	\mathbf{}
Tipo de máquina de escrever	Utilizado para compor letras do tipo máquina de escrever vertical.	\mathtt{}

8.2. Comandos de fonte de texto em matemática

Embora as declarações de fonte de texto como \rmfamily não possam ser usadas em matemática, os comandos de mudança de fonte - por exemplo,\textrm - podem ser usados ​​em texto e matemática. Usando esses comandos, você pode alternar temporariamente do contexto de matemática para o contexto de texto e digitar algum texto no meio da sua fórmula que logicamente faz parte do texto circundante fora da fórmula. A fonte usada para digitar este texto dependerá das condições circundantes, o que significa que herdará a codificação atual, a família, a série e a forma, como no exemplo abaixo.

\sffamily The result will be
\[ x = 10 \textbf{ and thus } y = 12 \]

Aqui podemos ver que a família sem foi mantida e a série foi alterada para ousada. O comando \text fornecido pelo pacoteamStext (que também é carregado por amsmath) pode ser mais útil. Ele pega os valores atuais de codificação, família, séries e formas sem alterar nenhum deles.

8.3. Versões de fórmula matemática

Discutimos como alterar partes de uma fórmula usando identificadores de alfabetos matemáticos. O LATEX também permite que você altere a aparência de uma fórmula como um todo. As fórmulas de matemática são sempre complicadas em uma certa versão matemática *. E você pode alternar entre as versões matemáticas fora do modo matemático usando o comando \mathversion, que altera o layout geral das fórmulas a seguir.

O LATEX possui duas versões matemáticas por padrão: Normal e BOLD . E pacotes especiais fornecem mais versões. Por exemplo, o pacoteMathTime(para o comercial MathTime fontes) configura uma versão de matemática chamadapesadopara fórmulas Typenet com símbolos Ultra Bold, conforme fornecido pelas fontes MathTime.

Obviamente, a versão matemática padrão é \mathVersion {Normal}. A versão em negrito, por sua vez, produzirá caracteres e símbolos mais ousados ​​do alfabeto, embora grandes operadores, como \sum, não sejam alterados por padrão. O exemplo abaixo mostra a mesma fórmula primeiro no normal e depois na versão em matemática em negrito.

\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}
\mathversion{bold}
\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}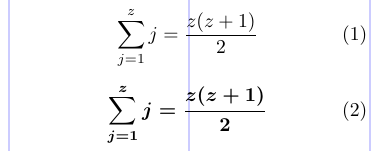

O uso de \mathVersion pode ser adequado em determinadas situações, como nos títulos, mas você deve ter em mente que mudar a versão significa alterar a aparência e possivelmente o significado de toda a fórmula. Se você deseja escurecer apenas alguns símbolos ou caracteres em uma fórmula, use o identificador de alfabetos \mathbf para caracteres e/ou use o comando \bm fornecido pelo pacote BM, em vez de alterar o\mathversion.

Quando você altera a versão matemática, o LATEX procura em suas tabelas internas para descobrir onde estão localizados todos os símbolos desta nova versão matemática. Também pode alterar todos ou alguns dos identificadores de alfabetos matemáticos e associá -los a outras formas de fonte nesta versão.

Mas o que acontece com os identificadores de alfabeto personalizados como \msfsl, que definimos no exemplo? Desde que você os declarasse usando \declaremathalphabet, eles permanecerão os mesmos em todas as versões de matemática.

Se o identificador de alfabetos matemáticos produzir uma fonte diferente em uma versão de matemática especial, você deve contar o LATEX usando o comando \setMathalphabet. Por exemplo, na configuração padrão, o identificador de alfabetos \mathsf é definido da seguinte forma:

\DeclareMathAlphabet{\mathsf}{OT1}{cmss}{m}{n}
\SetMathAlphabet{\mathsf}{bold}{OT1}{cmss}{bx}{n}

A primeira linha define Computer Modern Sans meio como padrão para \mathsf em todas as versões de matemática. A segunda linha instrui o LATEX a usar Computer Modern Sans Bold estendido na versão em negrito de matemática.

\SetMathAlphabet{cmd}{version}{encoding}{family}{series}{shape}

Como você deve ter adivinhado no exemplo anterior, \setMathalphabet recebe seis argumentos: o identificador do alfabeto matemático, o nome da versão matemática para o qual você está definindo uma configuração especial e quatro parâmetros para identificar a fonte com a qual está associando sua configuração.

Como observamos anteriormente, você pode redefinir um identificador de alfabetismo de matemática existente usando \declaraMathalphabet. Se você o fizer, todas as declarações anteriores de \setMathalphabet para este identificador são removidas da memória interna do LATEX. Portanto, o identificador será o mesmo em todas as versões de matemática, a menos que você adicione novas declarações \setMathalphabet.

8.4. Tuning Fontes em fórmulas com pacotes AMS-Latex

O pacote *amsfonts *(e *amssymb *) define dois alfabetos de matemática: o alfabeto Euler Fraktur (\mathfrak) e o alfabeto ousado do quadro -negro (\mathbb). Veja o exemplo abaixo.

\usepackage{amsfonts}
% -------------------------------------------------------------------------------
$ \forall n \in \mathbb{N} : \mathfrak{M}_n \leq \mathfrak{A} $

5. Estilo de fonte matemática ousada. O pacote BM

Somente para cartas latinas, você pode usar o comando \mathbf. Para todo o resto, há o pacote BM. Basta carregá -lo e usar \bm para tornar qualquer fórmula tão ousada e bonita quanto as fontes disponíveis.

O exemplo a seguir mostra muitas maneiras de usar os comandos \bm e \mathbf. Ele também mostra uma estratégia para definir nomes de taquigrafia para símbolos ousados ​​com frequência, usando \newCommand do LATEX padrão e \bmdefine, que é fornecido pelo pacote BM. Observe que \mathbf {xy} não é idêntico a \bm {xy}. O primeiro produz romano ousado “xy” e o último produz “*** xy***” (ousado matemática em itálico).

\usepackage{amsmath,amssymb,bm}
\newcommand\bfB{\mathbf{B}} \newcommand\bfx{\mathbf{x}}
\bmdefine\bpi{\pi} \bmdefine\binfty{\infty}
% -------------------------------------------------------------------------------
\section{The bold equivalence
  $\sum_{j < B} \prod_\lambda : \bm{\sum_{x_j} \prod_\lambda}$}
\begin{gather}
  B_\infty + \pi B_1 \sim \bfB_{\binfty} \bm{+} \bpi \bfB_{\bm{1}}
    \bm {\sim B_\infty + \pi B_1}\\
  B_\binfty + \bpi B_{\bm{1}} \bm{\in} \bm{\biggl\lbrace}
    (\bfB, \bfx) : \frac {\partial \bfB}{\partial\bfx}
    \bm{\lnapprox} \bm{1} \bm{\biggr\rbrace}
\end{gather}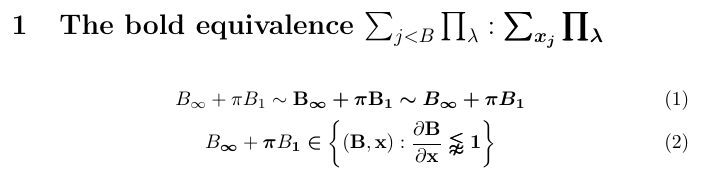

Neste exemplo, BM tenta o melhor para atender às solicitações de versões ousadas de símbolos e letras individuais. Mas se você olhar de perto, verá que os resultados nem sempre serão ótimos. Por exemplo, a soma e os operadores de produtos são feitos com uma técnica conhecida como ousado do homem pobre, no qual o símbolo é impressionado três vezes com ligeiras compensações. Além disso, os colchetes encaracolados não são feitos ousados. Tais desvantagens não podem ser evitadas porque, para alguns símbolos, simplesmente não há variante em negrito ao usar as fontes de matemática de computador **.

Quais são as regras exatas que \bm segue para produzir formas ousadas dos símbolos em seu argumento? Em geral, ele usa o fato de que o LATEX inclui uma versão em negrito ** (acessível via \boldmath) para digitar uma fórmula inteira em negrito (desde que as fontes em negrito adequadas estejam disponíveis e configuradas). Para cada símbolo, o comando \bm olha para esta versão matemática para ver o que seria feito nessa versão. Se a fonte selecionada para o símbolo for diferente da selecionada na versão matemática normal, ela digita o símbolo nesta fonte em negrito, obtendo um resultado perfeito (assumindo que a versão em matemática em negrito foi configurada corretamente). Se as fontes em ambas as versões forem idênticas, pressupõe que não exista uma variante em negrito e aplique o pobre homem do homem.

Carregue o pacote bm depois dos pacotes que alteram a configuração de fonte matemática existente!

A situação é ainda mais complexa com delimitadores, como \biggl \lbrace no exemplo. O Tex normalmente digita um delimitador por um glifo escolhido para corresponder a uma altura solicitada a partir de uma sequência de tamanhos diferentes. Esses glifos podem estar localizados em fontes diferentes e um tamanho específico pode ou não ter variantes em negrito. Tudo isso juntos torna impossível para \bm determinar de maneira confiável se ele precisa aplicar ousado o homem pobre. Portanto, digita o delimitador usando as fontes que são oferecidas pela versão em negrito de matemática. Com as fontes de matemática modernas ** do computador, apenas o menor tamanho de delimitador está disponível em negrito; Todos os outros tamanhos vêm de fontes que não têm variantes ousadas.

\usepackage{bm}
% -------------------------------------------------------------------------------
$\bm{\Biggl\lbrace\biggl\lbrace\Bigl\lbrace\bigl \lbrace \lbrace
  \mathcal{Q}
  \rangle \bigr\rangle\Bigr\rangle\biggr\rangle
\Biggr\rangle}$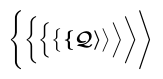

Normalmente, se um comando que ele próprio assume argumentos estiver dentro do argumento \bm, esse comando deve ser totalmente incluído no argumento de \bm. Como resultado, todas as partes do material do tiposejo estarão em negrito. Se você precisar da saída de um comando com argumentos apenas parcialmente em negrito, você deve fazer o seguinte. Você deve colocar o (s) símbolo (s) de que não deseja ser ousado em um \mbox e redefinir explicitamente a versão matemática dentro do conteúdo da caixa usando \unbollmath. Tex considera um \mbox como um símbolo da classe *comum *. Assim, para acertar o espaçamento, você pode ter que cercá -lo por um \mathbin, \mathrel ou \mathop.

\usepackage{amsmath,bm}
% -------------------------------------------------------------------------------
$ \bm{\sqrt[2]{x \times \alpha}} $ but
$ \bm{\sqrt[2]{x \mathbin{\mbox{\unboldmath$\times$}} \alpha}} $
or the similar
$ \bm{\sqrtsign}{\bm{x} \times \bm{\alpha}} $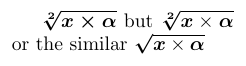

Felizmente, essas operações complexas raramente são necessárias. Na maioria dos casos, envolvendo comandos com argumentos, apenas partes do argumento precisam ser ousadas. E isso pode ser alcançado usando o comando \bm dentro desses argumentos. Assim como em \sqrtsign no exemplo anterior, para o caso comum de detalhes em negrito,\bm é especialmente programado para permitir que o argumento do sotaque esteja fora de seu próprio argumento. No entanto, se você precisar de tais sotaques regularmente, é melhor definir suas próprias abreviações, como no exemplo abaixo. *** Melhorando o desempenho***

Although \bmdefine\bpi{\pi}appears to be simply shorthand for \newcommand\bpi{\bm{\pi}}, in fact the truth is almost the opposite: \bm defines a new hidden temporary command using \bmdefineand then immediately uses this temporary command to produce the bold symbol. Em outras palavras, \bmdefine faz todo o trabalho duro! Se você frequentemente usa, por exemplo, algo que é definido via \bm {\ alpha}, então um novo \bmdefine será executado sempre. Se você fornecer a definição \bmDefine \ Balpha {\ alpha} no preâmbulo, então \bmdefine faz seu trabalho consumidor apenas uma vez, não importa quantas vezes \ Balpha seja usado.

\usepackage{bm}
\bmdefine\bhat{\hat}
% -------------------------------------------------------------------------------
$\hat a \neq \bm{\hat a} \neq \bm\hat a = \bhat a\neq \bm\widehat a$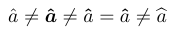

Este exemplo também mostra que os sotaques de largura variável (por exemplo, \widehat) compartilham uma deficiência com os delimitadores: na configuração do computador moderno, eles vêm de uma fonte para a qual nenhuma variante em negrito está disponível.