9. Símbolos nas fórmulas matemáticas | Manual de LaTeX

As tabelas neste artigo listam a grande variedade de símbolos matemáticos fornecidos pelos pacotes AMS-Latex, incluindo comandos para acessar cada símbolo. Eles também incluem os símbolos suplementares da fonte St Mary Road, projetada por Allan Jeffrey e Jeremy Gibbons. Este pacote se estende Computer Modern e AMS Symbol Font Collections e normalmente deve ser carregado além do AMSSyMB, mas sempre depois dele. Ele fornece símbolos extras para campos como programação funcional, álgebra de processo, teoria do domínio, lógica linear e muito mais.

As tabelas indicam quais pacotes extras precisam ser carregados para usar cada comando de símbolo. Os símbolos com nomes de comando em preto estão disponíveis no LaTeX padrão. Os símbolos com nomes de comando em azul requerem carregar amsmath, amssymb ou stmaryrd. Se Nesessário, a classificação adicional é dada por marcas: (stm) significa um símbolo de stMaryrd quando a tabela também contém símbolos de outros pacotes; (kernel) marca símbolos disponíveis no LaTeX padrão, mas apenas combinando dois ou mais glifos, enquanto um único glifo existe no pacote indicado; e (var) marca “símbolos alfabéticos” (do tipo \mathalpha) que mudam a aparência quando usados ​​no escopo de um identificador de alfabetismo matemático.

9.1. Aulas de símbolo de matemática de LaTeX

A classificação primária dos símbolos matemáticos está relacionada ao seu significado no uso técnico. Na tipografia matemática, essa classificação define o layout da fórmula. Em particular, o formatador de matemática da Tex ajusta o espaço horizontal em ambos os lados de cada símbolo de acordo com sua classe matemática. Essa classificação também faz algumas distinções mais refinadas, por exemplo, entre sotaques e símbolos simples e em quebrar a enorme lista de símbolos de Relation em várias tabelas.

A configuração para a matemática coloca cada símbolo em uma dessas clases: Ordinary (ord), Operator (op), Binary (bin), Relation (rel), Opening (Open), Closing (Close) ou Punctuation (Punct). A classe do símbolo pode ser alterada explicitamente usando os comandos \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathopen e \mathpunct. No próximo exemplo, \# e \top (ambos ORD por padrão) são alterados para um rel e um op.

\usepackage[fleqn]{amsmath}
\[ a \# \top _x^\alpha x^\alpha_b \]
\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]

Além das classes acima, certas subformulas - as frações mais importantes e as produzidas por \left e \right - formam uma classe chamada interna, que está explicitamente disponível no comando \mathinner.

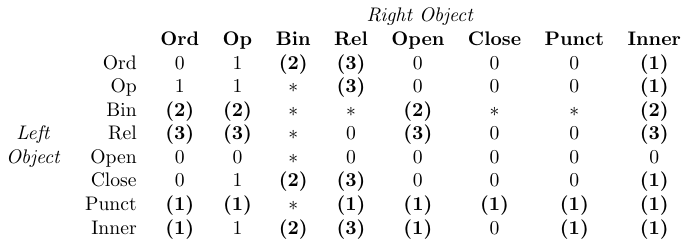
Na tabela, “0” significa “sem espaço”, “1” significa \thinmuspace, “2” significa \medmuskip, “3” significa \thickmuskip, “*” significa “impossível”. As entradas a negrito significam que o espaçamento correspondente não é adicionado nos estilos de escrita matemática.

A Tex lida com o espaçamento nas fórmulas simplesmente identificando a classe de cada objeto em uma fórmula e adicionando espaço entre cada par de objetos adjacentes, conforme definido pela tabela anterior. Esta tabela é codificada nas rotinas de matemática do Tex e, portanto, não pode ser alterada por pacotes de macro.

Um símbolo binary é transformado em um símbolo * comum * sempre que não é precedido e seguido por símbolos de uma natureza compatível com uma operação binária. É por isso que algumas entradas na tabela são marcadas como impossíveis. Por exemplo, $ +x $ dá +x(um unário mais) e não +x. Este último pode ser produzido por $ {}+x $.

Considere a seguinte fórmula (os valores padrão são alterados para mostrar os espaços adicionados mais claramente):

thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[
a - b = -\max \{ x , y \}
\]

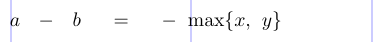
Tex identifica os objetos como Ord, Bin, Ord e assim por diante, e depois insere espaços da seguinte maneira:

 A      -      b      =      -    \max   \{   x    ,       y   \}
Ord \: Bin \: Ord \; Rel \; Ord \, Op   Open Ord Punct \, Ord Close

O menos na frente de \max é transformado em um *comum *porque um *binário *não pode seguir uma relação * *.

Em uma construção “\esquerda ... \ right “, toda a subformula delimitada pela construção se torna um único objeto de classe *interno *. Por outro lado, comandos como \bigl e \bigr produzem símbolos individuais das classes *de abertura *e *fechando *, respectivamente. A diferença entre eles é revelada na tabela de espaçamento acima. Embora possam resultar em delimitadores de tamanho vertical igual, as diferenças de espaçamento podem surgir, dependendo de objetos adjacentes na fórmula. Por exemplo, Ordinary seguido de abertura não recebe espaço, enquanto comum seguido por interno é separado por um espaço fino. Os espaços dentro da subformula dentro de uma construção “\ \ esquerda ... \ right “são feitos como esperado, começando com um símbolo * de abertura * e terminando com um símbolo fechando.

\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]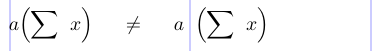

Em resumo, é melhor verificar se um símbolo pertence à classe desejada, em vez de apenas procurar nas mesas que se seguem.

9.2. Cartas, números e outros símbolos * comuns *

As cartas latinas ascii não acentuadas e dígitos de números árabes são todos chamados de “símbolos alfabéticos”. A fonte em que eles são digitados pode variar. Nas fórmulas de matemática, a fonte padrão para cartas latinas é itálica, enquanto para os dígitos árabes é vertical/romano. Os símbolos alfabéticos são todos de classe *ordinária *.

Ao contrário das letras latinas, as letras gregas matemáticas não estão mais intimamente relacionadas aos glifos usados ​​para digitar o texto grego normal. Devido a um curioso acaso do século XVIII, na principal tradição européia da tipografia matemática, a fonte padrão para letras gregas minúsculas nas fórmulas de matemática é itálico, enquanto para as letras gregas em maiúsculas é vertical/romano. (Em física e química, por exemplo, as tradições tipográficas são um pouco diferentes.)

As letras gregas da capital nas primeiras fileiras da tabela a seguir também são símbolos alfabéticos cuja fonte varia, com o padrão sendo vertical/romano. Existem letras gregas capitais, cada uma das quais tem a mesma aparência que alguma letra latina (por exemplo, a e alpha, b e beta, k e kappa, o e omicron). Essas cartas não estão presentes na tabela. Pela mesma razão, não há omicron minúsculo. Na prática, as letras gregas que parecem letras latinas não são usadas nas fórmulas de matemática.

Os símbolos a azul requerem o pacote amssymb. ^(var) indica um símbolo alfabético variável.

A próxima tabela lista outros símbolos em forma de carta da classe Ordinary. Os quatro primeiros são cartas hebraicas.

Os símbolos a azul requerem o pacote amssymb. ^(var) indica um símbolo alfabético variável.

A tabela seguinte lista os símbolos restantes na classe * Ordinária *, incluindo alguma pontuação comum. Eles se comportam como letras e dígitos, para que nunca tenham espaço extra ao seu redor.

Os símbolos a azul requerem o pacote amssymb ou, se sinalizados com ^(StM), o pacote stmaryrd.

Note que o sinal de exclamação, o ponto final e o ponto de interrogação não são tratados como pontuação nas fórmulas.

Sinónimos: negação lógica - \lnot, \neg; | - \vert, |; || - \Vert, \|.

Um erro comum é usar esses símbolos diretamente como operadores binários ou símbolos de relação, sem usar um comando de símbolo matemático corretamente definido para esse tipo. Assim, se você usar comandos como \#, \square ou \& , verifique com cuidado se você obtém os espaços inter-símbolos corretos ou, melhor ainda, defina seu próprio comando de símbolo.

\usepackage[fleqn]{amsmath} \usepackage{amssymb}
\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
% -------------------------------------------------------------------------------
\[ a \neg b \qquad x \square y + z \]
\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
\[ a \bneg b \qquad x \rsquare y + z \]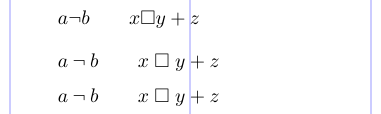

O comando \declaraMathSymbol é usado para declarar seu próprio nome de símbolo.

\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}

O primeiro argumento é o nome do comando escolhido. O segundo argumento é um dos comandos correspondentes à classe de símbolos. O terceiro argumento identifica a fonte do símbolo da qual o símbolo deve ser buscado. O quarto argumento fornece a posição do símbolo na codificação da fonte, um valor decimal, octal ou hexadecimal. Os valores corretos para os argumentos podem ser mais facilmente encontrados, observando as definições no arquivo amssymb.sty ou fontmath.ltx (para os símbolos do núcleo). Por exemplo, procuramos \neq e \square, substituímos o \mathord em cada caso e finalmente demos ao símbolo resultante um novo nome.

9.3. Detalhes em matemática

A tabela abaixo lista os comandos de sotaque disponíveis nas fórmulas. A maioria deles é definida no Standard Tex. Veja aqui para obter informações sobre sotaques extensíveis. Quando você adiciona um sotaque matemático a um símbolo, o resultado é um símbolo de classe comum.

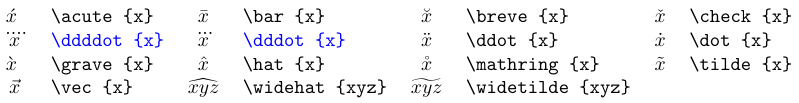
Os acentos a azul requerem o pacote amsmath.

Os dois últimos acentos estão disponíveis em diversas larguras, sendo a maior adequada utilizada automaticamente.

\usepackage{amstext}
% -------------------------------------------------------------------------------
\[ a = b \text{ but } a \tilde{=} b
\text{ which is not } a \mathrel{\tilde{=}} b \]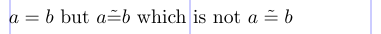

Outras maneiras de colocar símbolos sobre Relation Símbolos são mostrados aqui. Ao adicionar um sotaque a um i ou * j * nas fórmulas de matemática, é melhor usar as variantes sem pontos \iMath e \jmath.

9.4. Símbolos do operador binário

Existem mais de 100 símbolos de classe binary para escolher. A maioria deles está listada na tabela a seguir. Alguns deles também estão disponíveis como símbolos * de relação *, embora em nomes diferentes.

Os símbolos a azul requerem o pacote amssymb ou, se sinalizados com ^(StM), o pacote stmaryrd.

Os triângulos esquerdo e direito também estão disponíveis como símbolos de Relação.

O pacote stmaryrdaltera, de forma confusa, os símbolos Binários \bigtriangleup e \bigtriangledown para Operadores, deixando apenas os sinónimos \varbigtriangleup e \varbigtriangledown para as formas de operadores Binários.

O pacote AMSSyMB oferece alguns símbolos de caixa para uso como operadores * binários *; Muitos mais são adicionados por stmaryrd. Veja a próxima tabela.

Todos os símbolos requerem o pacote amssymb ou, se sinalizado com ^(StM), o pacote stmaryrd.

Você pode carregar o pacote stMaryrd com a opção heavycircles. Como resultado, cada comando de símbolo do círculo da próxima tabela que começa com \var troca sua definição com o comando correspondente sem o” var “; Por exemplo, o símbolo \varodot se torna \ odot e vice -versa.

Os símbolos a azul requerem o pacote amssymb ou, se sinalizado com ^(StM), o pacote stmaryrd.

A opção heavycircles do pacote stmaryrdafecta todos os comandos que começam por \var e as suas variantes normais.

9.5. Símbolos de relação

A classe de símbolos binários * de relação * é ainda grande que a dos operadores * binários *. A próxima tabela lista símbolos para igualdade e ordem. Uma barra pode ser colocada através de qualquer símbolo * de relação * precedendo -o com o comando \não. O símbolo negado representa o complemento (ou negação) das relações.

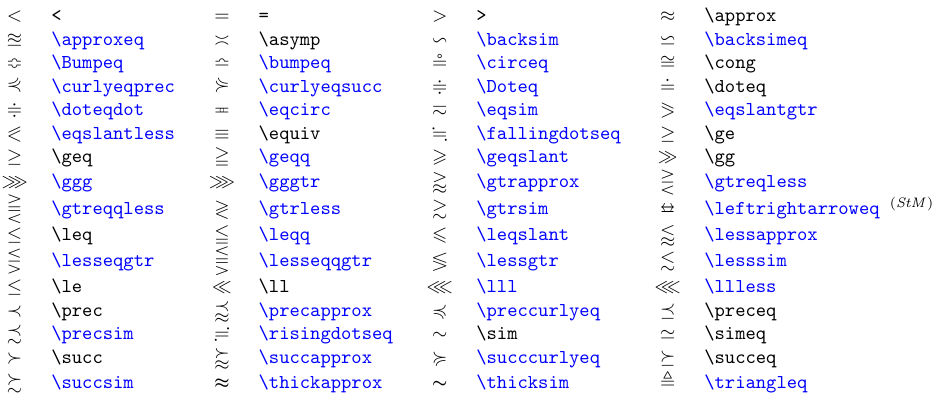
Os símbolos a azul requerem o pacote amssymb ou, se sinalizado como ^(StM), o pacote stmaryrd.

$ u \not< v$ or $a \not\in \mathbf{A} $

Esse método genérico de negar um símbolo Relation nem sempre fornece bons resultados, especialmente com símbolos maiores, porque a barra sempre será do mesmo tamanho, posição e inclinação. Devido a esse fato, alguns “símbolos negados” especialmente projetados também estão disponíveis. Veja a lista na próxima tabela.

Os símbolos a azul requerem o pacote amssymb.

Se uma opção estiver disponível, geralmente é preferível usar os glifos especialmente projetados. Para ver o porquê, compare os símbolos no próximo exemplo.

\usepackage{amssymb}
% -------------------------------------------------------------------------------
$ \not\leq \ \not\succeq \ \not\sim $ \par
$ \nleq \ \nsucceq \ \nsim $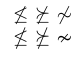

A próxima tabela lista os símbolos Relation para conjuntos e inclusões.

Os símbolos a azul requerem o pacote amssymb ou, se sinalizado com ^(StM), o pacote stmaryrd.

E agora negações da Relation símbolos para conjuntos e inclusão.

Os símbolos a azul requerem o pacote amssymb.

A tabela seguinte lista os símbolos * de seta Relation . Algumas construções extensíveis de seta que produzem símbolos compostas de relação são descritas aqui.

Os símbolos a azul requerem o pacote amssymb ou, se sinalizado com ^(StM), o pacote stmaryrd.

E aqui estão os símbolos negados em forma de flecha * *.

Os símbolos a azul requerem o pacote amssymb.

Existem outros elementos (além de `\não ‘usados ​​para negar os símbolos gerais * de relação *) que foram especialmente projetados para negar ou estender símbolos semelhantes a seta. Veja a próxima tabela.

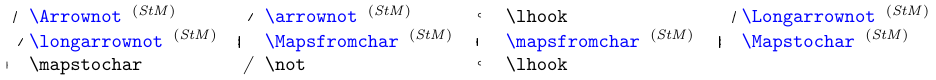
Os símbolos a azul requerem o pacote stmaryrd.

Estes símbolos são para combinação, principalmente com setas; por exemplo, \longarrownot\longleftarrow.

Utilize \joinrel para “colar” símbolos relacionais, por exemplo, \lhook\joinrel\longrightarrow.

As dimensões destes símbolos tornam-nos inadequados para outros usos.

\usepackage{stmaryrd}
% -------------------------------------------------------------------------------
$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$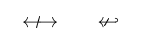

Finalmente, abaixo estão outros símbolos diversos * de relação *.

Os símbolos de Relação a azul requerem o pacote amssymb.

\therefore é um símbolo de Relação, pelo que o seu espaçamento pode não ser o esperado em utilizações comuns.