Разделители | Руководство по LaTeX | Aspose.TeX

Какой бы большой ни была математическая формула, TeX знает способ сделать некоторые символы достаточно большими, чтобы они имели правильный внешний вид. Например, результат ввода

$$\sqrt{1+\sqrt{1+\sqrt{1+
            \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+x}}}}}}}$$

показывает множество доступных радикальных знаков или знаков квадратного корня:

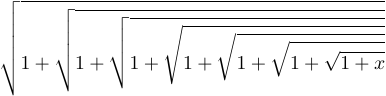
Три крупнейших знака здесь одинаковы, за исключением вертикального сегмента, который повторяется столько раз, сколько необходимо для достижения необходимого размера. В то же время знаки меньшего размера представляют собой отдельные символы, взятые из математических шрифтов TeX.

Нечто подобное происходит с круглыми скобками и другими так называемыми символами-разделителями. Такие символы важны в математике, поскольку они дают визуальные подсказки к основной структуре сложных выражений. Другими словами, они ограничивают границы отдельных подформул. Вот список из 22 основных разделителей, предоставляемых LaTeX:

Чтобы получить немного увеличенную версию любого из этих символов, просто введите \bigl или \bigr для открытия или закрытия разделителей соответственно. Это упрощает чтение формул с вложенными разделителями:

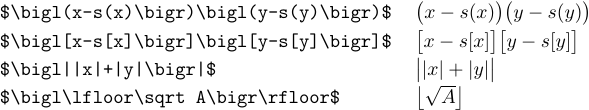
Разделители \big достаточно крупнее обычных, чтобы можно было заметить разницу, и в то же время достаточно малы, чтобы их можно было использовать в тексте абзаца:

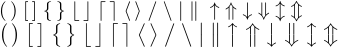
Вы можете получить еще один размер символов, подходящих для отображения, если наберете \Bigl и \Bigr вместо \bigl и \bigr:

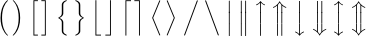
Они на 50 % выше, чем версии на предыдущем шаге. В отображаемых формулах часто используются еще более длинные разделители (в два раза больше \big). Вы можете получить их, набрав \biggl и \biggr:

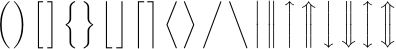
Наконец, вы можете ввести версии \Biggl и \Biggr, которые в 2,5 раза длиннее разделителей \bigl и \bigr:

LaTeX также предоставляет команды \bigm, \Bigm, \biggm и \Biggm для создания разделителей, которые можно использовать в середине формул. Такой разделитель действует как отношение, поэтому TeX помещает немного места по обе стороны от него:

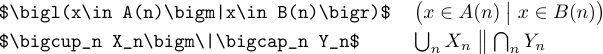
Также можно сказать просто \big, \Big, \bigg или \Bigg, чтобы создать разделитель, который ведет себя как обычная переменная. Эти команды в основном будут использоваться с косыми и обратными косыми чертами:

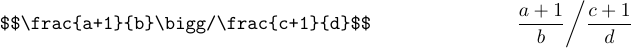
TeX реализует алгоритм, который определяет, какой высоты должна быть пара разделителей, чтобы включить данную подформулу. Вы можете использовать его вместо того, чтобы решать, должен ли разделитель быть \big, \bigg или каким-то еще. Просто скажи

\left<delim1><subformula>\right<delim2>

и TeX наберет подформулу, поставив указанные разделители слева и справа. Размер разделителей будет достаточно большим, чтобы покрыть подформулу:

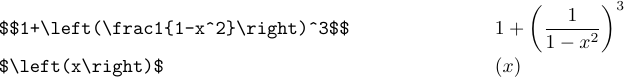
Когда вы используете \left и \right, они должны быть объединены в пары, так же, как фигурные скобки группируются. Вы не можете использовать \left в одной подформуле и \right в другой. Кроме того, вы не можете вводить такие вещи, как \left(...{...\right...} или \left(...\begingroup...\right)...\endgroup. Это связано с тем, что TeX необходимо набрать подформулу, которая появляется между \left и \right, прежде чем он сможет решить, насколько большими должны быть разделители. Если вы не используете \left и \right, вы этого не сделаете. t должны совпадать с круглыми скобками. Таким образом, вы можете ввести что-то вроде $[0,1)$ или $)($ или даже $)$. И даже если вы используете \left и \right, вам не обязательно сопоставлять определенные символы, так что \left) или \right( не вызовут ошибку.

Но зачем изучать \bigl, \bigr и другие подобные, если TeX может автоматически рассчитывать размеры для \left и \right? Есть как минимум три случая, когда вам следует самостоятельно решить, какой размер разделителя выбрать:

(1) Просто сравните следующие две формулы:

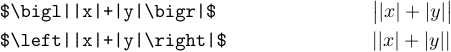
Действительно, использование \left и \right было неразумным выбором, поскольку они не могли определить размер разделителя, подходящий для лучшей читаемости.

(2) С другой стороны, иногда \left и \right выбирают разделитель большего размера, чем вам нужно. Чаще всего это происходит, когда в дисплей помещают крупного оператора:

Алгоритм TeX заставляет \left и \right заключать \sum вместе с его пределами, но в особых случаях, подобных этому, лучше оставить ограничения немного вытянутыми. Так что разделители \bigg здесь лучше.

(3) Когда вам нужно набрать огромную отображаемую формулу, вам придется разбить ее на две или более строк. И вы хотите убедиться, что его открывающий и закрывающий разделители имеют одинаковый размер; но вы не можете использовать \left в первой строке и \right в последней, поскольку \left и \right должны встречаться парами. Единственное решение — использовать \Biggl (например) в первой строке и \Biggr в последней.

Although \left and \right usually can make arbitrarily large delimiters, the slashes and angle brackets do have a maximum size. If you ask for really big versions of those symbols you will get the largest ones available.

Вы также можете использовать трюк, который создает так называемый нулевой (пустой) разделитель. Такой разделитель понадобится вам, когда вам нужно набрать формулу, которая визуально содержит только один большой разделитель. Например,

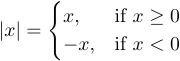
есть ‘{’, но нет ‘}’. Его можно изготовить с помощью конструкции вида

$$|x|=\left\{ ... \right.$$ 

где \right. генерирует правый нулевой разделитель.

LaTeX также предоставляет еще несколько разделителей, которые не включены в базовый набор из 22, поскольку они являются своего рода особенными. Команды \arrowvert, \Arrowvert и \bracevert создают разделители, состоящие из повторяющихся частей вертикальных стрелок, двойных вертикальных стрелок и больших фигурных скобок, соответственно, без наконечников стрелок или фигурных частей скобок. Они дают результаты, аналогичные \vert и \Vert, но они окружены большим количеством пробелов и имеют другой вес. Существуют также \lgroup и \rgroup, которые состоят из фигурных скобок без средних частей; и \lmoustache и \rmoustache, которые создают верхнюю и нижнюю половины больших фигурных скобок. Вот дисплеи с версиями \Big и \bigg \vert, \Vert и этими семью специальными разделителями:

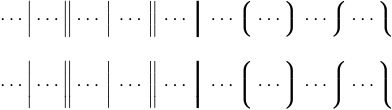
Вы можете обнаружить, что \lgroup и \rgroup похожи на жирные круглые скобки с более острыми изгибами по углам; это делает их привлекательными для некоторых больших дисплеев. Обратите внимание, что вы не можете использовать их точно так же, как круглые скобки, поскольку они доступны только в размерах \Big и более.