7. Предварительная настройка макета | Руководство по LaTeX

Обычно LaTeX отлично справляется с составлением математических формул. Но иногда необходима более тонкая настройка позиционирования. В этой статье обсуждаются некоторые методы тонкой настройки макета, чтобы сделать математические формулы немного лучше.

7.1. Автоматический размер и интервал

Математические символы и буквы обычно становятся меньше (и с меньшими интервалами), когда они появляются в виде дробей, нижних или верхних индексов. Математические формулы можно оформить в восьми математических стилях TeX:


D, D'	`\displaystyle`	Отображаются в отдельных строках
T, T'	`\textstyle`	Встроены в текст
S, S'	`\scriptstyle`	В верхних или нижних индексах
SS, SS'	`\scriptscriptstyle`	Во всех верхних или нижних индексах высшего порядка

Стиль текста (T) используется на верхнем уровне формулы, заданной в бегущем тексте (между парой $ или между $ и $), а стиль отображения используется на верхний уровень отображаемой формулы (между парой $$ или между \[ и \]). Что касается подформул, стиль можно определить по следующей таблице:


D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

Следующий пример иллюстрирует различные стили:

 1\normalsize                 %% Style:
 2\[ b                        %% D
 3    ^0                      %% S
 4   +                        %% D
 5   \frac{(k + p)            %% T
 6          _{j'}             %% S'
 7         % \displaystyle
 8         \pm                %% T [D]
 9         \frac{(f + q)      %% S [T]
10                ^{(pk)      %% SS [S]
11                   ^y       %% SS
12                   _{j'}}}  %% SS'
13              {(h + y)}}    %% S' [T']
14        {(l + q)            %% T'
15          ^{(pk)}}          %% S'
16\]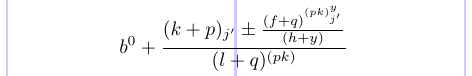

$Различные математические стили$

Вы можете удалить символ комментария (%) перед \displaystyle и посмотреть, как некоторые стили изменились на стили в скобках:

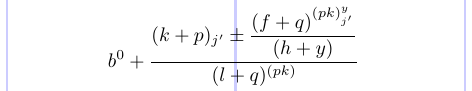
$Явно измененные математические стили$

Он показывает, как явно указать стиль, который будет использоваться в каждой части.

7.2. Подформулы

В тексте пара фигурных скобок обозначает группу или область, в которой действует какое-либо объявление. Внутри математической формулы они, кроме того, выделяют подформулу, которая всегда оформляется как отдельная сущность, добавляемая к внешней формуле. Как следствие, подформулы всегда набираются с естественной шириной и не растягиваются и не сжимаются по горизонтали, когда TeX строит абзац, пытаясь уместить формулу в строку. Мы уже показали, что подформула из простой группы фигурных скобок обрабатывается так, как если бы это был один символ. Это означает, что пустая группа создает невидимый символ, который может изменить интервал.

Содержимое нижних/надстрочных индексов и аргументы многих (но не всех) команд, таких как \frac и \mathrel, также являются подформулами. Таким образом, они получают такое же особое отношение. Например, аргумент \bm не обязательно задается как подформула, и это одно из важных исключений. Если в математической формуле вам нужно только ограничить область объявления, определите группу, используя \begingroup и \endgroup. Помните, что специализированные математические объявления, такие как изменения стиля, применяются до конца текущей подформулы, независимо от того, присутствуют ли какие-либо другие группы.

7.3. Большие разделители

LaTeX определяет четыре команды — \big, \Big, \bigg и Bigg - для обеспечения прямого управления размерами расширяемых разделителей. Они принимают один аргумент, который должен быть расширяемым разделителем, и создают более крупные версии разделителя, в 1,2–3 раза превышающие базовый размер.

Также существует три варианта для каждой из четырех команд, дающих четыре размера Открывающего символа (\bigl, \Bigl, \biggl и \Biggl); четыре размера символа связи (\bigm, \Bigm, \biggm и \Biggm); и четыре размера Закрывающего символа (\bigr, \Bigr, \biggr и \Biggr). Все 16 этих команд должны использоваться с любым символом, который может идти после \left, \right или (с eTeX) \middle (см. эту таблицу).

Размеры этих разделителей фиксированы в стандарте LaTeX. Однако в пакете amsmath размеры адаптируются к размеру окружающего материала в соответствии с размером шрифта и используемым математическим стилем. Это показано в примере ниже.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]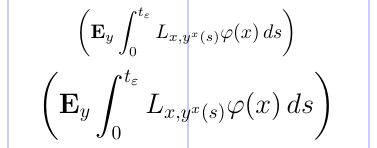

$Разграничители адаптируются к текущему размеру шрифта и математическому стилю$

7.4. Корректировка индекса по радикалу

Размещение индекса по радикальному знаку не всегда удачно в стандартном LaTeX. Однако вы можете использовать команды \leftroot и \uproot, определенные в пакете amsmath, чтобы настроить расположение этого индекса. Положительные целочисленные аргументы этих команд перемещают индекс влево и вверх соответственно, а отрицательные аргументы перемещают его вправо и вниз. Эти аргументы задаются в математических единицах, которые довольно малы, поэтому эти команды подходят для тонкой настройки.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4  \sqrt[\beta]{k} \qquad
5  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]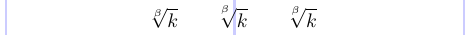

$Корректировка индекса радикального знака$

7.5. Доработка со стойками и фантомами

Всякий раз, когда вы хотите «идеально» набрать математические интервалы и выравнивание, обычно лучше обратиться к уникальным и расширенным возможностям примитивного TeX. Доступ к этим функциям обеспечивается рядом команд, связанных с \phantom и \smash. Эти команды можно использовать либо в математических формулах, либо в бегущем тексте.

Давайте посмотрим на следующий пример:

 1\usepackage{amsmath}
 2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
 3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
 4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
 5\newcommand\bfE{\mathbf{E}}
 6% -------------------------------------------------------------------------------
 7\begin{equation} \begin{split}
 8  f_{h, \ve}(x, y)
 9    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
10    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
11    &\relphantom{=} {} + h \biggl[
12       \frac{1}{\tve}
13       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
14               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
15    &\relphantom{=} \phantom{{} + h \biggl[ }
16       \frac{1}{\tve}
17       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
18               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19                                            \vf(x) \,ds    \biggr) \biggr]
20\end{split} \end{equation}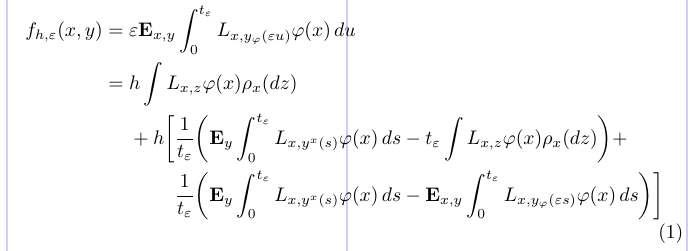

$Призраки формулы$

Здесь команда \phantom регулирует горизонтальное позиционирование. В преамбуле он используется для определения невидимого символа отношения, ширина которого равна его аргументу (в этом примере =). В математических средах он используется для выравнивания определенных строк, начиная их с «фантомной» или невидимой подформулы. Пустая пара фигурных скобок {} аналогична \mathord{}, которая создает невидимый символ нулевой ширины, необходимый для получения правильного интервала “+ h” (без {}, плюс знак выдаст унарный плюс с неподходящим пробелом перед h).

В отличие от \phantom, команда \smash верстает его содержимое (в LR-поле), но затем игнорирует их высоту и ширину, как если бы они оба были равны нулю. Команда \hphantom, определенная в стандарте LaTeX, представляет собой комбинацию этих двух. Он создает эквивалент \smash{\phantom{некоторое фантомное содержимое}}, то есть невидимый блок с нулевой высотой и глубиной, но с шириной фантомного содержимого.

Команда \vphantom аналогична, но она обнуляет ширину фантома, сохраняя его общую высоту и глубину. Команда \mathstrut определяется как \vphantom( и создает поле нулевой ширины, высота и глубина которого равна ширине скобки.

В пакете amsmath команда \smash может принимать необязательный аргумент, так что \smash[t]{...} игнорирует высоту содержимого блока, сохраняя глубину, а \smash[ b]{...} игнорирует глубину, сохраняя высоту.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

$Разрушение радикальных выражений$

Кажется, если придать y дополнительную высоту с помощью стойки, радикалы будут выглядеть одинаково. Но вместо этого они только выглядят еще более разными и в целом уродливыми. Оказывается, разбить нижнюю часть у — лучший способ.

В следующем примере показано очень распространенное использование разбивания. Команда \smash используется там для точного управления высотой окружающих разделителей. Это также показывает, что разрушение может вызвать проблемы, поскольку необходимо знать реальную высоту линии. Это исправляется с помощью \vphantom. \Hmjd — это составной символ, определяемый как:

1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Чтобы показать получившееся вертикальное пространство, мы добавили правила:

Внешний вид	`Код`	Комментарий
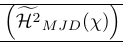$“Внешние скобки слишком большие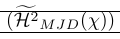”$	`\left( {\Hmjd } \right)`	Внешние скобки слишком большие
$“Внешние скобки слишком маленькие и линии слишком близко”$	`\left( \smash{\Hmjd } \right)`	Внешние скобки слишком маленькие и линии слишком близко
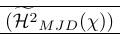$“В самый раз”$	`\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}`	В самый раз!
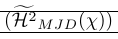$“Требуются и Vphantom, и частичный удар”$	`\left( \smash[t]{\Hmjd } \right)`	Требуются и `\vphantom`, и частичный удар

В некоторых местах недостатки низкоуровневой обработки TeX могут привести к ошибкам в мелких деталях набора. Это может произойти в определенных макетах, где (a) подформула (числитель/знаменатель дроби или нижний/верхний индекс) состоит ровно из одного LR-блока или аналогично сконструированного математического блока, а также (b) этот блок не имеет своего естественного размера, как в случае с более сложными формами \makebox, smashes и некоторыми фантомами.

Чтобы убедиться в этом, давайте посмотрим на следующий пример:

1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]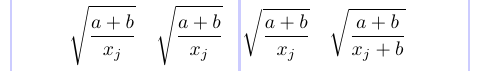

$Проблемы, вызванные ударами$

Чтобы уменьшить глубину радикала, во втором радикале был добавлен символ \smash, но это не дало никакого эффекта. В третьем радикале работало с пустой скобочной группой. Но в четвертом радикале пустая группа скобок не требовалась. Подводя итог: всякий раз, когда вы обнаружите, что \smash не работает, попробуйте добавить пустую математическую подформулу ({}) перед одиноким полем, чтобы ее обработать правильно.

7.6. Горизонтальный интервал

Более тонкая и более сложная настройка требует явных команд интервалов, показанных в следующей таблице:

$Команды горизонтального интервала$ Как полная, так и краткая формы этих команд надежны, и их также можно использовать вне математических формул в обычном тексте. Они связаны с тонким, средним и толстым пространством, доступным на машинах, использовавшихся для набора математики в середине 20 века.

Текущие значения трех параметров TeX \thinmuskip, \medmuskip и \thickmuskip определяют объем пространства, добавляемого этими командами \..space. Их значения по умолчанию с amsmath перечислены в таблице. Эти параметры низкого уровня требуют значений в математических единицах (мю). Следовательно, их можно установить только с помощью низкоуровневых назначений TeX, а не с помощью \setlength или чего-то подобного. Более того, обычно их значения не следует изменять, поскольку они используются внутри системы математического набора TeX (см. следующую таблицу).

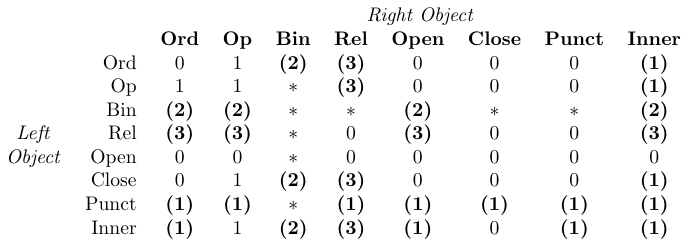
$Расстояние между символами$

В таблице 0 означает “нет пробела”, 1 означает \thinmuspace, 2 означает \medmuskip, 3 означает \thickmuskip, * означает “невозможно”. Записи, выделенные жирным шрифтом, означают, что соответствующий пробел не добавляется в математических стилях письма.

Одна математическая единица («1му») равна 1/18 em текущего размера математического шрифта. Отсюда следует, что абсолютное значение mu варьируется в зависимости от математического стиля, обеспечивая одинаковый интервал независимо от используемого стиля.

Текст в математических формулах Шрифты в математических формулах