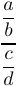5. Дроби, биномиальные коэффициенты и математические стили
Еще одна распространенная вещь, которую вы можете встретить в математических формулах, — это дроби и другие конструкции, в которых что-то вроде числителя помещается поверх чего-то вроде знаменателя. Примером последнего являются биномиальные коэффициенты.
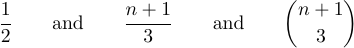
Вы можете получить эти три формулы в виде отображаемых уравнений, набрав $$1\over2$$ и $$n+1\over3$$ и $$\n+1\choose3$$.
Команда \over применяется ко всему в формуле, если вы не заключаете ее в определенную подформулу с помощью фигурных скобок, и в этом случае \over применяется ко всему в этой подформуле.

Вы не можете использовать \over дважды в одной и той же подформуле, т. е. введите \over b\over 2. Вместо этого вы должны явно указать, что над чем идет:

Кажется, что обе формулы выглядят не очень красиво. В таких случаях обычно лучше преобразовать дроби в «перечеркнутую форму». Например, последние две формулы следует набрать следующим образом:
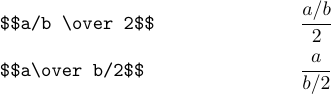
Вот более сложные примеры:
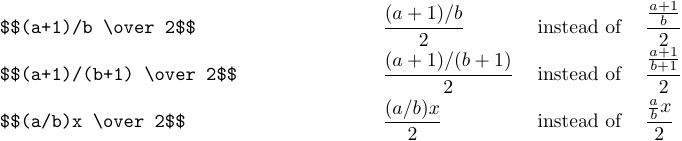
Глядя на приведенные выше примеры, вы, возможно, заметили, что буквы и другие символы иногда уменьшаются, когда они представлены в виде дробей, точно так же, как они становятся меньше, когда они находятся в нижних или верхних индексах. Давайте теперь поговорим о том, как TeX выбирает размеры символов. TeX имеет восемь стилей обработки формул:
- стиль отображения (для формул, отображаемых в отдельных строках)
- стиль текста (для формул, встроенных в текст)
- стиль сценария (для подформул, используемых в качестве верхних или нижних индексов)
- стиль сценария-скрипта (для надстрочных или нижних индексов второго порядка) и четыре «тесных» стиля, которые почти одинаковы, за исключением того, что нижние и верхние индексы не так сильно поднимаются. Мы будем называть восемь стилей D, D’, T, T’, S, S’, SS, SS’, где D — отображение. стиль, D’ — сжатый стиль отображения, T — стиль текста и т. д. TeX также использует три размера для ввода математических формул: размер текста, размер сценария и размер сценария сценария.
Чтобы набрать формулу в бегущем тексте, вы заключаете ее в $...$; это создаст формулу в стиле T. Или вы можете заключить его в $$...$$, чтобы получить отображаемую формулу; это отобразит формулу в стиле D. Подформулы формулы могут быть выполнены в разных стилях. Зная стиль, вы можете определить размер шрифта, который будет использовать TeX:

Не существует стиля «SSS», поскольку такие крошечные символы будут еще менее читабельными, чем символы сценария.

Например, если x^{a_b} должен быть набран в стиле D, a_b будет установлен в стиле S, а b — в стиле SS; результат:
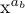
Мы пока не увидели никакой разницы между стилями D и T. На самом деле существует небольшая разница в расположении экспонент, хотя в каждом случае используется размер шрифта. Но существует большая разница между стилями D и T в случае дробей:

Итак, если вы наберете $1\over2$ (в тексте), вы получите стиль S вместо стиля S’. Но если вы наберете $$1\over2$$, вы получите стиль T вместо стиля T’ в отображаемой формуле.
Наконец, \underline не меняет стиль. Математические акценты, а команды \sqrt и \overline изменяют сжатые стили на их сжатые аналоги, сохраняя сжатые стили.
Может случиться так, что вам не понравится стиль, который TeX выбирает по своим правилам. Вы можете указать желаемый стиль, набрав \displaystyle или \textstyle или \scriptstyle или \scriptscriptstyle; выбранный стиль будет применяться до конца формулы или подформулы или до тех пор, пока вы не выберете другой стиль. Например, $$n+\scriptstyle n+\scriptscriptstyle n.$$ дает следующий результат:
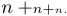
Это показывает, что знак плюс также уменьшается при изменении стиля и что TeX не ставит пробел вокруг + в стилях скриптов.
Давайте рассмотрим другой пример – цепную дробь.
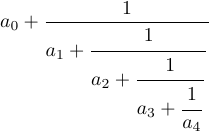
Вы можете получить его, набрав
1$$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$$Без \strut и \displaystyle в этой формуле результат был бы другим:
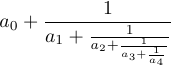
LaTeX определяет макрос \frac, который позволяет вам указывать дроби, используя другой синтаксис: \frac{a}{b} эквивалентен a\over b, а \frac12 эквивалентен 1\over2 .
В TeX есть еще одна операция \atop, похожая на \over, за исключением того, что она не рисует дробную линию:

Формат LaTeX также определяет \choose, который похож на \atop, но результат заключен в круглые скобки:
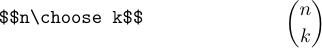
Он называется \choose, потому что это общепринятое обозначение биномиального коэффициента, который показывает, сколькими способами можно выбрать k вещей из n вещей.
Команды \over, \atop и \choose нельзя смешивать друг с другом. Например, $$n\choose k\over 2$$ недопустимо. Вы должны использовать группировку, чтобы получить либо $${n\choose k}\over2$$, либо $$n\choose{k\over2}$$.
В TeX есть команда \above, которая является обобщенной версией \over и \atop. В этой команде вы указываете точную толщину линии, набрав \above<dimen>. Например,
1$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$создаст сложную дробь с правилом толщиной 1 пт между дробями в числителе и знаменателе: