10. Популярные математические символы LaTeX и их спутники.

Самые популярные математические символы LaTeX

Символ суммирования LaTeX

Одним из ключевых символов, часто используемых в математических уравнениях, является символ суммирования. В следующем разделе мы рассмотрим использование и форматирование символа суммирования в LaTeX.

Символ суммирования, обозначаемый греческой буквой Сигма, используется для обозначения сложения ряда слагаемых. Это позволяет математикам кратко выражать такие понятия, как суммы, последовательности и ряды. В LaTeX символ суммирования можно легко включать в математические выражения с помощью специальных команд.

Использование символа суммы LaTeX

Чтобы использовать символ суммирования в LaTeX, используется команда \sum. Общий синтаксис следующий:

1\sum_{i=lower}^{upper} expression

Здесь переменная i представляет индекс суммирования. Нижний и верхний пределы определяют диапазон, в котором выполняется суммирование. Выражение, которое может содержать математические термины, суммируется.

Например, чтобы представить сумму чисел от 1 до 5, код LaTeX будет выглядеть так:

1$\sum_{i=1}^{5} i$

что приведет к следующему выводу:

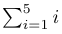
$Пример простого символа суммирования$

Символ ограничения LaTeX

Другой часто используемый математический символ LaTeX — это символ ограничения LaTeX. Ниже мы углубимся в его значение и использование в математических уравнениях.

Символ ограничения LaTeX, часто обозначаемый как lim, является фундаментальным математическим символом, используемым для описания поведения функции при приближении к определенному значению или бесконечности. Понимая команды LaTeX, связанные с этим символом, пользователи могут точно представлять пределы в своих математических выражениях.

Использование символа ограничения LaTeX

Чтобы сгенерировать символ ограничения в LaTeX, просто используйте команду \lim, за которой следуют любые необходимые дополнительные спецификации. Например, набрав

1$\lim_{x \to \infty}f(x)$

создаст символ ограничения с переменной x, приближающейся к бесконечности, следующим образом:

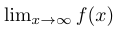
$Простой пример ограничения$

Это обозначение эффективно сообщает, что поведение функции наблюдается, когда входная переменная приближается к бесконечно большому значению.

В математических уравнениях предельный символ LaTeX играет решающую роль в выражении поведения и границ функций. Он позволяет исследователям, преподавателям и студентам точно описывать и анализировать математические понятия, такие как сходимость, непрерывность и дифференцируемость.

Кроме того, символ ограничения LaTeX можно комбинировать с другими символами и операторами для создания более сложных математических выражений. Например, использование символа ограничения в сочетании с символом суммирования позволяет пользователям выражать суммирование с переменными пределами. Эта гибкость и универсальность делают LaTeX бесценным инструментом для математического набора текста.

Ограничения LaTeX при математическом наборе текста

Ограничения символов в LaTeX позволяют пользователям определять границы или ограничения математических выражений. Они необходимы для точного представления таких понятий, как суммирование, интеграция и операции с произведением. Используя соответствующие команды LaTeX, пользователи могут устанавливать пределы символов, чтобы указать диапазон или поведение математических операций.

Чтобы проиллюстрировать ограничения символов в LaTeX, давайте рассмотрим в качестве примера символ суммирования. Символ суммирования обычно используется для выражения суммы ряда слагаемых. Используя команду \sum, пользователи могут генерировать символ суммирования. Однако для определения пределов суммирования требуются дополнительные команды. Например, набрав

1$\sum_{i=1}^n$

будет позиционировать нижний индекс как i=1, а верхний индекс как n. Это обозначение указывает, что операцию суммирования следует выполнять для значений i, начиная с 1 и заканчивая n.

Помимо позиционирования по умолчанию, LaTeX также позволяет пользователям настраивать размещение ограничений. Используя команду \limits, пользователи могут размещать пределы выше и ниже символа суммирования. Например, набрав

1$\sum\limits_{i=1}^n$

расположит пределы выше и ниже символа суммирования, обеспечивая более четкое представление. Это также поведение по умолчанию в режиме отображения. Таким образом

1$$\sum{i=1}^n$$

не требует \limits. Но чтобы вернуться к ограничениям в индексных позициях, требуется \nolimits.

Сравните варианты в таблице ниже:

$Ограничения на символы в разных положениях и режимах$

Символ большой суммы LaTeX

В этом разделе мы рассмотрим, как получить больший символ суммирования в LaTeX, используя пакет relsize. С помощью пакета relsize пользователи могут легко настроить размер математических символов, включая символ суммирования, в соответствии со своими конкретными потребностями.

Для начала пользователям необходимо включить пакет relsize в свой документ LaTeX, добавив в преамбулу следующую строку:

1\usepackage{relsize}

После включения пакета пользователи смогут использовать команду \mathlarger{} для получения увеличенной версии символа суммирования. Если вставить нужное выражение в фигурные скобки \mathlarger{}, символ суммирования будет отображаться в большем размере.

Рассмотрим следующий пример:

1\begin{equation*}
2\sin x = \mathlarger{\mathlarger{\sum}}_{n=0}^{\infty}(-1)^n\frac{x^{2n + 1}}{(2n + 1)!}
3\end{equation*}

что приводит к выводу ниже:

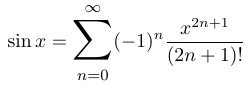
$Большой символ суммирования$

Как мы видим, пакет relsize в LaTeX предоставляет удобный способ получить больший символ суммирования. Включив пакет в преамбулу документа и используя команду \mathlarger{}, пользователи могут настроить размер символа суммирования в соответствии со своими конкретными потребностями.

LaTeX Символы LaTeX Таблицы