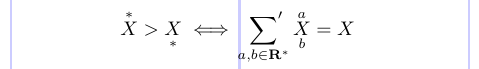4. Оформлені символи та складені конструкції | LaTeX

Пакет amsmath надає деякі команди для створення структур, таких як дробові об’єкти та декоровані символи. Це обговорення охоплює деякі з них.

4.1. Загальні дроби

Пакет amsmath визначає команду \genfrac, яка створює узагальнений дріб.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Перші два аргументи визначають лівий і правий роздільники відповідно. Використовуючи третій аргумент, thick, ви можете замінити стандартну товщину правила дробу. Наприклад, біномінальні коефіцієнти (див. нижче) використовують значення 0pt для цього аргументу, щоб зробити лінію невидимою. Стандартне значення (якщо не заповнено) товщини лінії визначається поточним налаштуванням шрифту для математичного набору. У наведеному нижче списку містяться стандартні значення, які використовуються в прикладах цієї статті.

Style	Default Thickness
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

Четвертий аргумент, стиль, замінює (якщо не залишити порожнім) математичний стиль для використовуваного макета та розміру шрифту. Значення має бути в діапазоні 0-3: 0 - \displaystyle, 1 - \textstyle, 2 - \scriptstyle, 3 - \scriptscriptstyle. Якщо цей аргумент залишити порожнім, стиль вибирається відповідно до звичайних правил для дробів. Останні два аргументи є чисельником і знаменником.

The old fraction commands \over, \overwithdelims, \atop, \atopwithdelims, \above, and \abovewithdelims, which standard LaTeX inherits from TeX, produce warnings when they are used with the amsmath package.

4.1.1. Прості дроби

Маючи команду \genfrac, пакет amsmath також визначає три команди як зручні скорочення: \frac, \dfrac і \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

Наведений нижче приклад демонструє використання цих команд:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.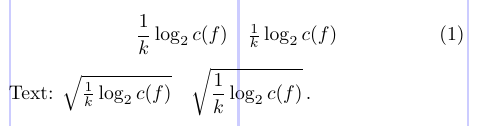

4.1.2. Біноміальні коефіцієнти

Ще одна структура, подібна до дробів, — біноміальні коефіцієнти. Щоб допомогти вам набрати їх, пакет amsmath надає подібні команди \binom, \dbinom і \tbinom.

Ось як вони скорочують команду \genfrac:

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

І ось приклад:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.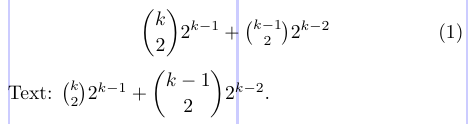

4.1.3. Суцільні дроби

Якщо вам потрібно набрати масив дробів, який, по суті, є нескінченним дробом, також відомим як «безперервний дріб», у пакеті amsmath є команда \cfrac. Передайте необов’язковий аргумент «[l]» або «[r]», щоб вирівняти чисельник ліворуч або праворуч, який за замовчуванням розміщено по центру.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}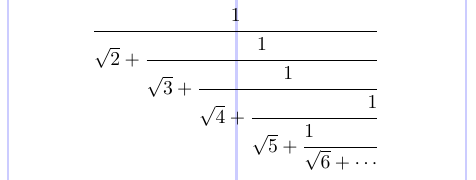

4.2. Математика в коробках

Пакет amsmath надає команду \boxed, подібну до \fbox, щоб помістити вміст математичних режимів у поле.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}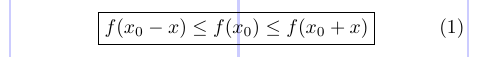

4.3. Позиціонування меж

Нижні та верхні індекси інтегралів, сум, добутків чи інших операторів можна розміщувати над і під математичним оператором («гранична позиція») або в нижньому/верхньому індексі праворуч від оператора. Як правило, рамки в тексті не використовуються (інакше рядки можуть розповзатися). У відображеній формулі розташування залежить від оператора. У наступному прикладі показано стандартне розміщення в LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.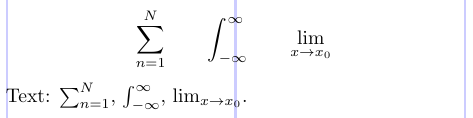

Пакет amsmath пропонує параметри керування позиціонуванням. Вони перераховані нижче, де default позначає поведінку, якщо пакунок amsmath використовується зі стандартним класом документа LaTeX, але без жодної з цих опцій.

intlimits, nointlimits	Розмістіть верхні/нижні індекси інтеграційних символів зверху та знизу або збоку (за замовчуванням) відповідно. Використовується лише у відображених формулах.
sumlimits, nosumlimits	Розташуйте верхні/нижні індекси великих операторів (сума, добуток тощо) зверху та знизу (за замовчуванням) або збоку відповідно. Використовується лише у відображених формулах.
namelimits, nonamelimits	Подібно до sumlimits або nosumlimits, але для певних операторів або «імен операторів», таких як inf, sup, lim, min, max, які традиційно набираються з індексами під ними, принаймні, коли вони зустрічаються у відображеній формулі.

TeX має три примітивні команди, які з’являються відразу після символу чи назви оператора, керують розташуванням нижніх/верхніх індексів: \limits, \nolimits і \displaylimits. Команда \displaylimits створює нижні/верхні індекси в граничній позиції, коли поточний математичний стиль є стилем відображення. Це типова поведінка, коли з’являється символ класу Operator або використовується команда \mathop. Якщо вам потрібно набрати оператор із нижніми/верхніми індексами в граничній позиції за межами дисплея, ви повинні оголосити його окремо за допомогою команди \limits.

Порівняйте наступний приклад із попереднім.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.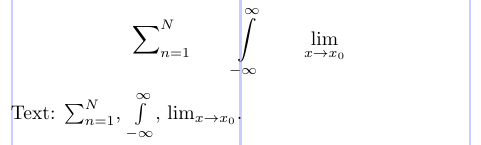

4.3. Кратні інтеграли

Щоб набрати кілька інтегральних знаків із добре відрегульованими пробілами між ними як у тексті, так і на дисплеях, використовуйте команди \iint, \iiint та \iiiint. \idotsint створює два цілісні знаки з крапками між ними.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}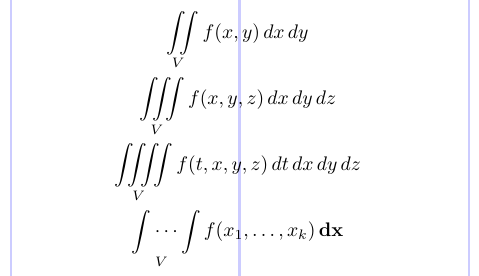

4.4. Модульні відносини

Нотація “mod” для класів еквівалентності цілих чисел регулюється спеціальними угодами про інтервали. Щоб впоратися з цим, пакет amsmath пропонує команди \mod, \bmod, \pmod і \pod. У наступному прикладі показано використання цих команд.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}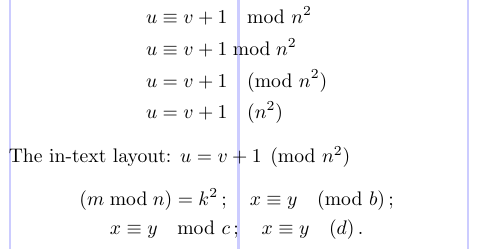

With amsmath, the spacing of \pmod is decreased within a non-displayed formula.

4.5. Математичні крапкові наголоси

Окрім математичних наголосів \dot і \ddot, пакет amsmath надає команди \dddot і \ddddot, які створюють потрійні та чотирикратні наголоси відповідно.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Створення верхнього індексу з наголосів: пакет amsxtra

Пакет amsxtra пропонує корисну функцію, набір простих команд для розстановки наголосів як верхніх індексів у підформулі:

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$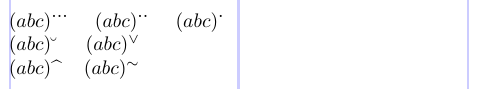

4.7. Інші прикраси

Стандартний LaTeX має команду \stackrel, яка розміщує верхній індекс над символом Відношення. Крім того, пакет amsmath визначає команди \overset і \underset. Використовуйте його, щоб розмістити матеріал над або під будь-яким Звичайним або Відношенням символом або Двійковим оператором.

Команда \sideset додає прикраси до будь-якого символу Operator (сума, добуток тощо) на додаток до звичайних обмежень. Вони розміщуються в нижньому та верхньому індексах ліворуч і праворуч від оператора.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]