Роздільники | Підручник з LaTeX | Aspose.TeX

Якою б великою не була математична формула, TeX знає спосіб зробити деякі символи достатньо великими, щоб мати належний вигляд. Наприклад, результат набору тексту

$$\sqrt{1+\sqrt{1+\sqrt{1+
            \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+x}}}}}}}$$

показує різноманітність доступних радикалів, або знаків квадратного кореня:

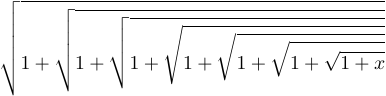
Три найбільші знаки тут однакові, за винятком вертикального сегмента, який повторюється стільки разів, скільки необхідно для досягнення необхідного розміру. У той же час менші знаки є різними символами, взятими з математичних шрифтів TeX.

Щось подібне відбувається з круглими дужками та іншими так званими символами «розділювачів». Такі символи важливі в математиці, оскільки вони дають візуальні підказки до основної структури складних виразів. Іншими словами, вони обмежують межі окремих підформул. Ось список із 22 основних роздільників, наданих LaTeX:

Щоб отримати трохи більшу версію будь-якого з цих символів, просто введіть \bigl або \bigr для відкриття або закриття роздільників відповідно. Це полегшує читання формул із вкладеними роздільниками:

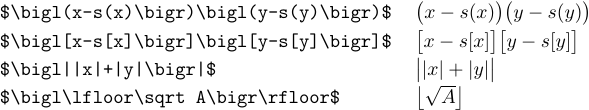
Роздільники \big достатньо більші, ніж звичайні, щоб можна було помітити різницю, і водночас достатньо малі, щоб використовувати їх у тексті абзацу:

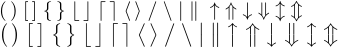
Ви можете отримати на один крок більші символи, придатні для дисплеїв, якщо введете \Bigl і \Bigr замість \bigl і \bigr:

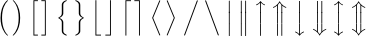
Вони на 50% вищі за версії на попередньому кроці. У відображених формулах часто використовуються навіть вищі розділювачі (вдвічі більші за \big). Ви можете отримати їх, ввівши \biggl і \biggr:

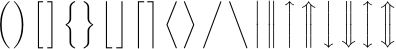
Нарешті, ви можете ввести версії \Biggl і \Biggr, у 2,5 рази вищі за розділювачі \bigl і \bigr:

LaTeX також надає команди \bigm, \Bigm, \biggm і \Biggm для створення роздільників, які можна використовувати в середині формул. Такий роздільник діє як відношення, тому TeX ставить трохи місця з обох боків від нього:

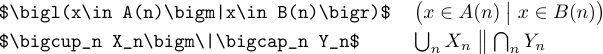
Також можна сказати просто \big, \Big, \bigg або \Bigg, щоб створити роздільник, який веде себе як звичайна змінна. Ці команди в основному використовуватимуться з похилими та зворотними похилими рисками:

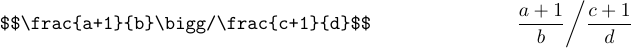
TeX реалізує алгоритм, який визначає, якої висоти має бути пара роздільників, щоб охопити дану підформулу. Ви можете використовувати його замість того, щоб вирішувати, чи має роздільник бути \big, \bigg чи будь-яким іншим. Просто скажи

\left<delim1><subformula>\right<delim2>

і TeX набере підформулу, розмістивши вказані розділювачі ліворуч і праворуч. Розмір роздільників буде достатньо великим, щоб охопити підформулу:

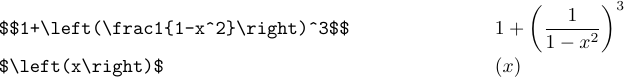
Коли ви використовуєте \left і \right, вони повинні бути об’єднані в пари, як фігурні дужки роблять групи. Ви не можете мати \left в одній підформулі та \right в іншій. Крім того, ви не можете вводити такі речі, як \left(...{...\right...} або \left(...\begingroup...\right)...\endgroup. Це відбувається тому, що TeX має набрати підформулу, яка з’являється між \left і \right, перш ніж він зможе вирішити, наскільки великими роздільники, коли ви не використовуєте \left і \right, ви не Тому вам дозволено вводити щось на зразок $[0,1)$ або $)($ або навіть $)$. І навіть якщо ви використовуєте \left і \right, вам не потрібно збігатися з окремими символами, щоб \left) або \right( не викликали помилки.

Але навіщо вивчати \bigl і \bigr та інші подібні, коли TeX може автоматично обчислювати розміри для \left і \right? Є принаймні три випадки, коли ви захочете самостійно вирішити, чи правильно вибрати розмір розділювача:

1. Просто порівняйте наступні дві формули:

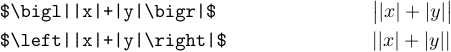
Дійсно, використання \left і \right не було мудрим вибором, оскільки вони не могли визначити розмір роздільника, який підходить для найкращої читабельності.

2. З іншого боку, іноді \left і \right вибирають більший роздільник, ніж вам потрібно. Це відбувається переважно, коли вони містять великий оператор на дисплеї:

Алгоритм TeX змушує \left і \right охоплювати \sum разом із його обмеженнями, але в особливих випадках, подібних до цього, виглядає краще дозволити обмеженням трохи звисати. Тому роздільники \bigg тут кращі.

3. Коли вам потрібно набрати величезну відображену формулу, вам доведеться розбити її на два або більше рядків. І ви хочете переконатися, що його відкриваючі та закриваючі роздільники мають однаковий розмір; але ви не можете використовувати \left у першому рядку та \right в останньому, оскільки \left та \right мають зустрічатися парами. Єдиним рішенням є використання \Biggl (наприклад) у першому рядку та \Biggr в останньому.

Хоча \left і \right зазвичай можуть створювати як завгодно великі роздільники, косі риски та кутові дужки мають максимальний розмір. Якщо ви попросите дійсно великі версії цих символів, ви отримаєте найбільші з доступних.

Ви також можете скористатися трюком, який створює так званий нульовий (порожній) роздільник. Такий роздільник знадобиться, коли потрібно набрати формулу, яка візуально містить лише один великий роздільник. Наприклад,

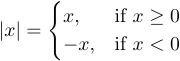
має “{”, але не має “}”. Його можна виготовити за допомогою конструкції форми

$$|x|=\left\{ ... \right.$$ 

де \right. створює правий нульовий розділювач.

LaTeX також надає кілька додаткових розділювачів, які не перераховані в основному наборі з 22, оскільки вони є певними особливостями. Команди \arrowvert, \Arrowvert і \bracevert створюють розділювачі, створені з повторюваних частин вертикальних стрілок, подвійних вертикальних стрілок і великих дужок, відповідно, без наконечників стрілок або фігурних частин дужок. Вони дають результати, подібні до \vert і \Vert, але вони оточені більшим пробілом і мають іншу вагу. Є також \lgroup і \rgroup, які побудовані з дужок без середніх частин; і \lmoustache і \rmoustache, які утворюють верхню та нижню половини великих дужок. Ось відображення з версіями \Big і \bigg \vert, \Vert і цими сімома спеціальними роздільниками:

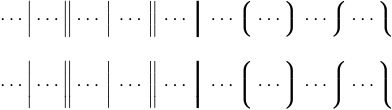
Ви можете виявити, що \lgroup і \rgroup схожі на жирні круглі дужки з різкішими вигинами в кутах; це робить їх привабливими для деяких великих дисплеїв. Зауважте, що ви не можете використовувати їх так само, як круглі дужки, оскільки вони доступні лише у розмірах \Big і більше.