9. Відображені рівняння
Наразі ми обговорили, як працювати з окремими формулами; але дисплеї часто включають цілу купу різних формул або різних частин величезної формули, і може бути складно розмістити їх так, щоб вони належним чином узгоджувалися одна з одною. На щастя, великі дисплеї зазвичай підпадають під кілька простих моделей.
9.1. Однорядкові дисплеї
Відображені рівняння часто містять звичайний текст. Ми вже
обговорювали те, як використовувати латинський шрифт у формулах, не виходячи з математичного режиму, але найкращий спосіб отримати текст на дисплеї — це помістити його в \hbox. Насправді математика взагалі не потрібна. Набір типів
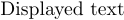
ви можете сказати $$\hbox{Відображений текст}$$. Але ось більш цікавий приклад:

У цьому випадку формули та текст були об’єднані таким чином:
1$$\X_n=X_k \qquad\hbox{if and only if}\qquad
2 Y_n=Y_k \quad\hbox{and}\quad Z_n=Z_k.$$Як бачите, \qquad з’являється навколо “якщо і тільки якщо”, але один \quad оточує “і”; це акцентує увагу на тому, що частини Y і Z на дисплеї тісніше пов’язані одна з одною, ніж з частиною X.
Давайте подивимося на такий дисплей:
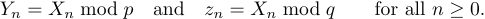
Одним із способів його визначення є
1$$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all }n\ge0.$$Але краще було б (див. другий рядок)
1$$Y_n=X_n\bmod p \quad\hbox{and}\quad z_n=X_n\bmod q
2 \qquad\hbox{for all $n\ge0$.}$$Так, це математичний режим у горизонтальному режимі в математичному режимі дисплея, але це рішення виглядає природніше, ніж перше.
Тепер давайте повернемося до чисел рівнянь, тих маленьких міток, які з’являються збоку від дисплеїв. Якщо ви друкуєте
1$$<formula>\eqno<formula>$$TeX відобразить першу формулу, а також розмістить номер рівняння (друга формула) на правому полі. Наприклад,
1$$x^2-y^2 = (x+y)(x-y).\eqno(15)$$буде виробляти
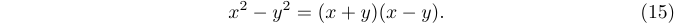
Ви також можете отримати числа рівнянь на лівому полі за допомогою \leqno. Наприклад,
1$$x^2-y^2 = (x+y)(x-y).\leqno(15)$$буде виробляти
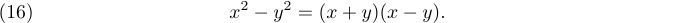
Зверніть увагу, що ви завжди ставите номер рівняння другим, навіть якщо він з’являється ліворуч.
Відображені рівняння відцентровані незалежно від наявності номерів рівнянь. Але коли формула велика, TeX гарантує, що вона не заважає її номеру; номер рівняння може навіть бути розміщений на окремому рядку.
LaTeX також надає середовище рівнянь для автоматичної нумерації ваших рівнянь. Наприклад, набір тексту
1\begin{equation}
2 f(x)=(x+a)(x+b)
3\end{equation}призводить до
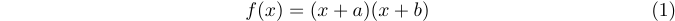
Також можна позначати рівняння та посилатися на них за допомогою \label і \ref. Наприклад,
1\begin{equation} \label{eq:someequation}
2 f(x)=(x+a)(x+b)
3\end{equation}
4this references equation \ref{eq:someequation}.призводить до
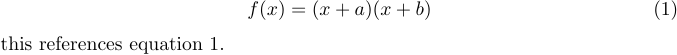
9.2. Багаторядкові дисплеї
Іноді дисплей може не відповідати простому шаблону однорядкової формули з номером рівняння або без нього. LaTeX надає спеціальні команди для більшості решти випадків.
Багаторядкові дисплеї зазвичай містять кілька рівнянь, які слід вишикувати за допомогою знаків «=», як у
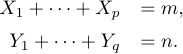
Рекомендованим методом для такого відображення є використання середовища array, наданого LaTeX:
1$$\begin{array}{rl}
2 X_1+\cdots+\X_p&=m,\\
3 Y_1+\cdots+\Y_q&=n.}
4\end{array}$$Це середовище допоможе вам представити свої рівняння у вигляді прямокутного масиву з кількома стовпцями (у цьому випадку два стовпці). Рядки містять окремі рівняння, розділені командою \\ (це символ нового рядка). Ліва та права частини кожного рівняння розділені символом “&”. Не обов’язково, щоб останній рядок закінчувався на \\. Середовище також має аргумент, який визначає вирівнювання в кожному стовпці. У прикладі відповідним значенням є rl, що означає, що ліві частини рівнянь будуть розташовані врівень праворуч, тоді як праві частини будуть розташовані врівень зліва.
LaTeX також надає середовище eqnarray*, яке працює аналогічно, але для правильного вирівнювання обох сторін рівнянь потрібні дві точки вирівнювання, і, на жаль, інтервали дещо виходять за рамки математичних умов друку. Наступний код
1\begin{eqnarray*}
2 X_1+\cdots+X_p&=&m,\\
3 Y_1+\cdots+Y_q&=&n.
4\end{eqnarray*}створює наступний результат:
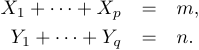
Середовище eqnarray LaTeX дає той самий результат, за винятком того, що воно автоматично нумерує рівняння.
У середовищі масиву може бути будь-яка кількість рівнянь; загальна закономірність така
1\begin{array}{rl}
2 <left-hand side_1>&<right-hand side_1>\\
3 <left-hand side_2>&<right-hand side_2>\\
4 ...
5 <left-hand side_n>&<right-hand side_n>
6\end{array}де кожна <права сторона> починається з символу, за яким потрібно виконати вирівнювання.
Результатом середовища array є квадрат із вертикальним центром. Це дозволяє легко отримати формулу, як
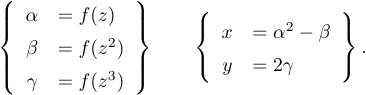
Ви просто використовуєте середовище array двічі в рядку:
1$$\left\{
2 \begin{array}{rl}
3 \alpha&=f(z)\\ \beta&=f(z^2)\\ \gamma&=f(z^3)
4 \end{array}
5\right\}\qquad\left\{
6 \begin{array}{rl}
7 x&=\alpha^2-\beta\\ y&=2\gamma
8 \end{array}
9\right\}.$$Наступний рівень складності виникає, коли у вас є кілька вирівняних рівнянь з кількома номерами рівнянь. Або деякі рядки можуть бути пронумеровані, а інші ні:
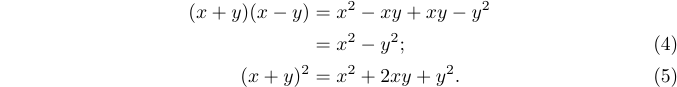
На жаль, навіть із середовищем eqnarray* (з його неправильним інтервалом) неможливо вручну вказати числа рівнянь у багаторядковому дисплеї. Тільки пакет amsmath може
допомогти. Отже, рекомендований спосіб отримати наведений вище результат - це ввести:
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}Якщо ви пропустите і \tag, і \notag у рядку середовища align, номер рівняння буде згенеровано автоматично з використанням поточного значення, що зберігається у відповідному внутрішньому лічильнику.
Якщо ви завантажите пакет amsmath з опцією leqno, номери рівнянь з’являться на лівому полі. Таким чином
1%% Preamble
2\usepackage[leqno]{amsmath}
3%% Body
4\begin{align}
5 (x+y)(x-y)&=x^2-xy+xy-y^2 \notag \\
6 &=x^2-y^2; \tag4\\
7 (x+y)^2 &=x^2+2xy+y^2. \tag5
8\end{align}виробляє
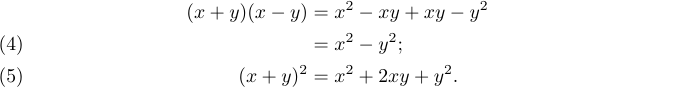
Щоб дізнатися більше про набір математичних формул за допомогою можливостей пакета amsmath, перегляньте ці
статті.
9.3. Довгі формули
Тепер давайте обговоримо, що робити, якщо формула настільки довга, що не вміщується в один рядок. Наприклад, припустімо, що ви зіткнулися з рівнянням
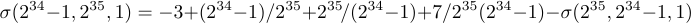
Вам доведеться якось його розбити; TeX зробив усе можливе, щоб стиснути все разом, зменшивши пробіли біля знаків «+» і «-» до нуля, але рядок все одно вийшов переповненим.
Давайте спробуємо розірвати це рівняння перед «+7». Середовище array залишає занадто багато місця праворуч від ‘=’, якщо ви використовуєте його так само, як і для багаторядкових рівнянь:
1$$\begin{array}{rl}
2 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
3 &\qquad{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1)
4\end{array}$$Отже, найкраще знову вдатися до пакета amsmath. Але цього разу вам слід використовувати масив align*, оскільки номери рівнянь не потрібні:
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sigma(2^{34}-1,2^{35},1)&=-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1) \\
6 &\qquad+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).
7\end{align*}$$Це дає
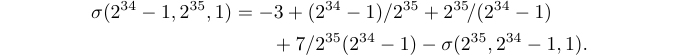
Ідея полягає в тому, щоб розглядати довгу однорядкову формулу як дворядкову, використовуючи \qquad у другому рядку, щоб друга частина формули відображалася праворуч від знака ‘=’ у першому рядку.
Насправді це непросте завдання вирішити, як розбити довгі показані формули на рядки; TeX ніколи не намагається зробити це, тому що жоден набір правил не є дійсно адекватним. Автор математичного рукопису, як правило, найкращий суддя щодо того, що робити, оскільки позиції розриву залежать від тонких факторів математичних викладів. Наприклад, часто бажано підкреслити певну симетрію чи іншу структуру, яка лежить в основі формули, і такі речі вимагають чіткого розуміння того, що саме відбувається у цій формулі.
Тим не менш, можна сформулювати кілька емпіричних правил щодо того, як працювати з довгими формулами на дисплеях, оскільки є деякі принципи, яких найкращий математичний верстальник прагне дотримуватися:
Хоча формули в абзаці завжди розриваються після бінарних операцій і зв’язків, відображені формули завжди розриваються перед двійковими операціями та зв’язками. Ось чому ми не закінчили перший рядок нашого попереднього прикладу
(2^{34}-1)+; ми закінчили його на(2^{34}-1і почали другий рядок на+.Якщо рівняння розривається перед двійковою операцією, другий рядок має починатися принаймні на два квадрати праворуч від того місця, де в першому рядку починається внутрішня підформула, що містить цю бінарну операцію. Наприклад, якщо ви хочете зламати
1$$\sum_{0<k<n}\left(<formula_1>+<formula_2>\right)$$біля знака «плюс» між <formula_1> і <formula_2> майже обов’язково, щоб знак «плюс» у другому рядку знаходився дещо правіше великої лівої дужки, яка відповідає \left(.
У щойно розглянутому прикладі потрібно особливо ретельно розбити формулу на два рядки, оскільки розділювачі \left і \right не можна використовувати окремо: ви не можете мати лише \left в одному рядку формулу та лише \right у другому. Крім того, вам потрібно, щоб два розділювачі були однакового розміру, навіть якщо вони розташовані в різних рядках. Зазвичай найкращим рішенням є вибір розміру роздільника самостійно; наприклад, ви можете ввести
1%% Preamble
2\usepackage{amsmath}
3%% Body
4\begin{align*}
5 \sum_{0<k<n}\biggl(&<formula_1>\\
6 &\qquad+<formula_2>\biggr)
7\end{align*}якщо роздільники \bigg найкращі. Зверніть увагу, що маркери & не зустрічаються біля знаків = у цьому прикладі, вони просто позначають точку вирівнювання.
Є ще один спосіб розбити довгі формули, який іноді називають дворядковою формою. Ідея полягає в тому, щоб розмістити першу частину формули майже врівень зліва, а другу частину – майже врівень праворуч, де «майже врівень» означає «одну квадро». Таким чином, розглянута раніше дволінійна форма довгого сигма-рівняння є
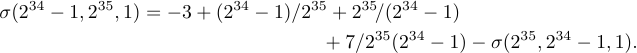
Щоб отримати цей дворядковий ефект, просто введіть:
1$$\displaylines{\quad\sigma(2^{34}-1,2^{35},1)
2 =-3+(2^{34}-1)/2^{35}+2^{35}\!/(2^{34}-1)\hfill{}\cr
3\hfill{}+7/2^{35}(2^{34}-1)-\sigma(2^{35},2^{34}-1,1).\quad\cr}$$Тут у другому рядку було введено додатковий {}, щоб TeX знав, що + є бінарною операцією. Дворядкова форма особливо рекомендована для рівнянь, які мають довгу ліву частину; у цьому випадку розрив зазвичай ставиться безпосередньо перед знаком =.