7. Коригування попереднього розміру макета | LaTeX

Зазвичай LaTeX чудово справляється зі складанням математичних формул. Але іноді потрібна більш точна настройка позиціонування. У цій статті розглядаються деякі прийоми тонкого налаштування макета, щоб зробити математичні формули трохи кращими.

7.1. Автоматичне визначення розмірів і інтервалів

Математичні символи та літери зазвичай стають меншими (і з меншими інтервалами), коли вони з’являються у дробах, нижніх або верхніх індексах. Математичні формули можна викласти у восьми математичних стилях TeX:


D, D'	`\displaystyle`	Відображаються на рядках самостійно
T, T'	`\textstyle`	Вбудовано в текст
S, S'	`\scriptstyle`	У верхньому чи нижньому індексах
SS, SS'	`\scriptscriptstyle`	У всіх верхніх або нижніх індексах

Стиль тексту (T) використовується на верхньому рівні формули, яка встановлюється в поточному тексті (між парою $ або між $ і $), тоді як стиль відображення використовується на верхній рівень показаної формули (між парою $$ або між \[ і \]). Що стосується підформул, стиль можна визначити за такою таблицею:


D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

Наступний приклад ілюструє різні стилі:

 1\normalsize                 %% Style:
 2\[ b                        %% D
 3    ^0                      %% S
 4   +                        %% D
 5   \frac{(k + p)            %% T
 6          _{j'}             %% S'
 7         % \displaystyle
 8         \pm                %% T [D]
 9         \frac{(f + q)      %% S [T]
10                ^{(pk)      %% SS [S]
11                   ^y       %% SS
12                   _{j'}}}  %% SS'
13              {(h + y)}}    %% S' [T']
14        {(l + q)            %% T'
15          ^{(pk)}}          %% S'
16\]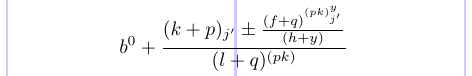

$Різні математичні стилі$

Ви можете видалити символ коментаря (%) перед \displaystyle і побачити, як деякі стилі змінилися на стилі в дужках:

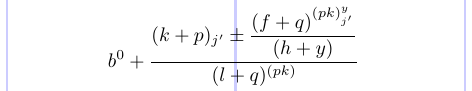
$Явно змінено математичні стилі$

Він показує, як явно вказати стиль, який буде використовуватися в кожній частині.

7.2. Підформули

У тексті пара фігурних дужок вказує на групу або область, у межах якої діє деяка декларація. У межах математичної формули вони, крім того, розмежовують підформулу, яка завжди набирається як окрема сутність, яка додається до зовнішньої формули. Як наслідок, підформули завжди набираються за своєю природною шириною і не розтягуються чи звужуються горизонтально, коли TeX створює абзац, намагаючись вмістити формулу в рядок. Ми вже показали, що підформула з простої групи дужок обробляється так, ніби це один символ. Це означає, що порожня група створює невидимий символ, який може змінити інтервал.

Вміст нижніх/верхніх індексів і аргументів багатьох (але не всіх) команд, таких як \frac і \mathrel, також є підформулами. Таким чином, вони отримують таке ж особливе ставлення. Аргумент \bm, наприклад, не обов’язково встановлюється як підформула, і це один із важливих винятків. У математичній формулі, якщо вам потрібно лише обмежити область оголошення, визначте групу за допомогою \begingroup і \endgroup. Пам’ятайте, що спеціалізовані математичні оголошення, такі як зміни стилю, застосовуються до кінця поточної підформули, незалежно від того, присутні інші групи чи ні.

7.3. Великі роздільники

LaTeX визначає чотири команди - \big, \Big, \bigg і Bigg - для забезпечення прямого керування розмірами розширюваних роздільників. Вони беруть єдиний аргумент, який має бути розширюваним роздільником, і створюють більші версії роздільника, від 1,2 до 3 базових розмірів.

Є також три варіанти для кожної з чотирьох команд, які дають чотири розміри початкового символу (\bigl, \Bigl, \biggl і \Biggl); чотири розміри символу зв’язку (\bigm, \Bigm, \biggm і \Biggm); і чотири розміри закриваючого символу (\bigr, \Bigr, \biggr і \Biggr). Усі 16 цих команд потрібно використовувати з будь-яким символом, який може стояти після \left, \right або (з eTeX) \middle (див. цю таблицю).

Розміри цих роздільників фіксовані в стандарті LaTeX. Однак у пакеті amsmath розміри адаптуються до розміру навколишнього матеріалу, відповідно до розміру шрифту та стилю математики, який використовується. Це показано на прикладі нижче.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]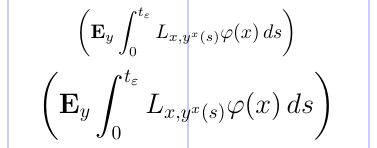

$Роздільники адаптуються до поточного розміру шрифту та математичних стилів$

7.4. Налаштування індексу на радикал

Розміщення індексу на знаку радикала не завжди добре в стандартному LaTeX. Однак ви можете використовувати команди \leftroot і \uproot, визначені в пакеті amsmath, щоб налаштувати позиціонування цього індексу. Додатні цілі аргументи цих команд переміщують індекс ліворуч і вгору, відповідно, а від’ємні аргументи — праворуч і вниз. Ці аргументи подано в математичних одиницях, які досить малі, тому ці команди підходять для точного налаштування.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4  \sqrt[\beta]{k} \qquad
5  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]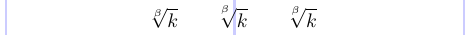

$Регулювання індексу радикального знака$

7.5. Тонка настройка зі стійками і фантомами

Щоразу, коли ви хочете «ідеально» набрати математичний інтервал і вирівнювання, зазвичай краще звернутися до унікальних і розширених можливостей примітивного TeX. Доступ до цих функцій забезпечується кількома командами, пов’язаними з \phantom і \smash. Ці команди можна використовувати або в математичних формулах, або в поточному тексті.

Давайте розглянемо такий приклад:

 1\usepackage{amsmath}
 2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
 3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
 4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
 5\newcommand\bfE{\mathbf{E}}
 6% -------------------------------------------------------------------------------
 7\begin{equation} \begin{split}
 8  f_{h, \ve}(x, y)
 9    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
10    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
11    &\relphantom{=} {} + h \biggl[
12       \frac{1}{\tve}
13       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
14               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
15    &\relphantom{=} \phantom{{} + h \biggl[ }
16       \frac{1}{\tve}
17       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
18               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19                                            \vf(x) \,ds    \biggr) \biggr]
20\end{split} \end{equation}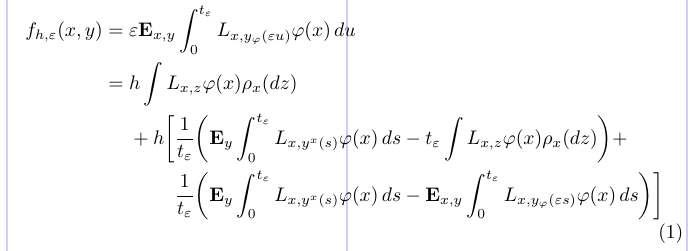

$Фантоми формули$

Тут команда \phantom регулює горизонтальне розташування. У преамбулі він використовується для визначення символу невидимого відношення, що дорівнює за шириною його аргументу (= у цьому прикладі). У математичних середовищах він використовується для вирівнювання певних рядків, починаючи їх із «фантомної» або невидимої підформули. Порожня пара дужок {} — це те саме, що \mathord{}, яка створює невидимий символ нульової ширини, необхідний для отримання правильного інтервалу «+ h» (без {}, плюс знак створить унарний плюс із невідповідним інтервалом перед h).

На відміну від \phantom, команда \smash набирає його вміст (у LR-блокі), але потім ігнорує їх висоту та ширину, ніби вони обидва дорівнюють нулю. Команда \hphantom, визначена в стандартному LaTeX, є комбінацією двох. Він створює еквівалент \smash{\phantom{деякий фантомний вміст}}, тобто невидиму коробку з нульовою висотою та глибиною, але шириною фантомного вмісту.

Команда \vphantom схожа, але вона робить ширину фантома нульовою, зберігаючи його загальну висоту плюс глибину. Команда \mathstrut визначається як \vphantom() і створює рамку нульової ширини, висота та глибина якої дорівнює висоті дужок.

У пакеті amsmath команда \smash може приймати необов’язковий аргумент, так що \smash[t]{...} ігнорує висоту вмісту коробки, зберігаючи глибину, тоді як \smash[ b]{...} ігнорує глибину, зберігаючи висоту.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

$Розбиваючи радикальний вираз$

Схоже, що надання y додаткової висоти за допомогою розпірки зробить радикали схожими. Але натомість це лише робить їх більш різними та потворнішими в цілому. Виявляється, найкраще розбити низ y.

У наступному прикладі показано дуже поширене використання smashing. Команда \smash використовується там, щоб забезпечити точне керування висотою оточуючих роздільників. Це також показує, що розбивання може спричинити проблеми, оскільки потрібно знати справжню висоту лінії. Це виправляється \vphantom. \Hmjd — складений символ, визначений як:

1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Щоб показати отриманий вертикальний простір, ми додали правила:

Зовнішній вигляд	`Код`	Коментар
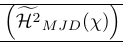$“Зовнішні дужки завеликі”$	`\left( {\Hmjd } \right)`	Зовнішні дужки завеликі
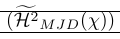$“Зовнішні дужки занадто малі та правила занадто близькі”$	`\left( \smash{\Hmjd } \right)`	Зовнішні дужки замалі, а правила надто близькі
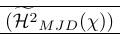$“Якраз”$	`\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}`	В самий раз!
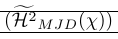$“Потрібні як Vphantom, так і Partial Smash”$	`\left( \smash[t]{\Hmjd } \right)`	Потрібні як `\vphantom`, так і частковий smash

У деяких місцях недоліки низькорівневої обробки TeX можуть призвести до помилок у тонких деталях набору. Це може статися в певних макетах, де (а) підформула (чисельник/знаменник дробу або нижній/верхній індекс) складається точно з одного LR-коробки або подібно сконструйованого математичного блоку, а також (б) цей блок не t матиме свій природний розмір, як і складніші форми \makebox, smashes і деякі фантоми.

Щоб побачити це, розглянемо такий приклад:

1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]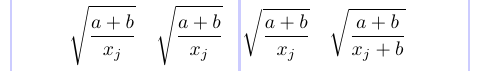

$Проблеми, спричинені руйнуванням$

Щоб зменшити глибину радикала, до другого радикалу було додано \smash, але це не мало ефекту. У третьому радикалі це спрацювало з порожньою фігурною дужкою. Але в четвертому радикалі порожня дужкова група не потрібна. Підводячи підсумок, щоразу, коли ви бачите, що \smash не працює, спробуйте додати порожню математичну підформулу ({}) перед самотньою рамкою, щоб її обробляли правильно.

7.6. Горизонтальний інтервал

Для більш тонкого та складного налаштування потрібні чіткі команди інтервалів, наведені в наступній таблиці:

$Команди горизонтального інтервалу$ І повна, і коротка форми цих команд є надійними, і їх також можна використовувати поза математичними формулами у звичайному тексті. Вони пов’язані з тонкими, середніми та товстими просторами, доступними на машинах, які використовувалися для набору математики в середині 20 століття.

Поточні значення трьох параметрів TeX \thinmuskip, \medmuskip і \thickmuskip визначають обсяг місця, доданого цими командами \..space. Їх стандартні значення з amsmath наведено в таблиці. Ці параметри низького рівня вимагають значень у математичних одиницях (mu). Тому їх можна встановити лише за допомогою низькорівневих призначень TeX, а не за допомогою \setlength чи подібного. Крім того, зазвичай їхні значення не слід змінювати, оскільки вони використовуються внутрішньо математичною версією TeX (див. наступну таблицю).

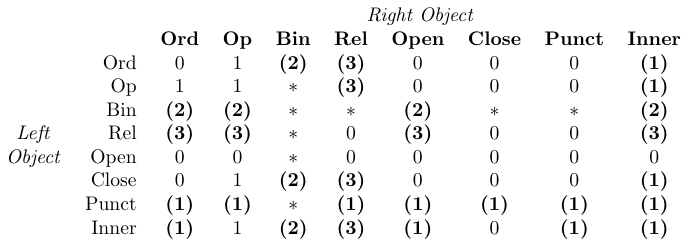
$Інтервал між символами$

У таблиці 0 означає «немає місця», 1 означає \thinmuspace, 2 означає \medmuskip, 3 означає \thickmuskip, * означає «неможливо». Записи, виділені жирним шрифтом, означають, що відповідний інтервал не додається в стилі математичних сценаріїв.

Одна математична одиниця (“1mu”) дорівнює 1/18 em у поточному розмірі математичних шрифтів. З цього випливає, що абсолютне значення mu змінюється залежно від математичного стилю, забезпечуючи послідовний інтервал незалежно від використовуваного стилю.

Текст у математичних формулах Шрифти в математичних формулах