9. Символи в математичних формулах | Підручник з LaTeX

У таблицях у цій статті перераховано великий діапазон математичних символів, що надаються пакетами AMS-LATEX, включаючи команди для доступу до кожного символу. Вони також містять додаткові символи зі шрифту St Mary Road, розробленого Алланом Джеффрі та Джеремі Гіббонсом. Цей пакунок розширює колекції символьних шрифтів Computer Modern і AMS і зазвичай має завантажуватися на додаток до amssymb, але завжди після нього. Він надає додаткові символи для таких областей, як функціональне програмування, алгебра процесів, теорія предметної області, лінійна логіка та багато іншого.

У таблицях зазначено, які додаткові пакети потрібно завантажити, щоб використовувати кожну символьну команду. Символи з назвами команд чорним кольором доступні в стандартному LaTeX. Символи з назвами команд синім кольором вимагають завантаження amsmath, amssymb або stmaryrd. Якщо необхідно, подальша класифікація надається позначками: ^(StM) означає символ із stmaryrd, коли таблиця також містить символи з інших пакетів; ^(kernel) позначає символи, які доступні в стандартному LaTeX, але лише шляхом поєднання двох або більше гліфів, тоді як один гліф існує у вказаному пакеті; і ^(var) позначає «алфавітні символи» (типу \mathalpha), які змінюють зовнішній вигляд під час використання в межах ідентифікатора математичного алфавіту.

9.1. Класи математичних символів

Основна класифікація математичних символів пов’язана з їх значенням у технічному використанні. У математичній типографіці ця класифікація визначає макет формули. Зокрема, математичний формат TeX регулює горизонтальний простір з обох боків від кожного символу відповідно до його математичного класу. Ця класифікація також робить деякі точніші відмінності, наприклад, між наголосами та простими символами та розбиває величезний список символів Зв’язок на кілька таблиць.

Налаштування для математики поміщає кожен символ в один із таких класів: Ordinary (Ord), Operator (Op), Binary (Bin), Relation (Rel), Opening (Open), Opening (Open), Закриття (Close), або Пунктуація (Punct). Клас символу можна явно змінити за допомогою команд \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathopen і \mathpunct. У наступному прикладі \# і \top (обидва Ord за замовчуванням) змінено на Rel і Op.

1\usepackage[fleqn]{amsmath}
2\[ a \# \top _x^\alpha x^\alpha_b \]
3\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]

$Явна зміна класу символів$

На додаток до наведених вище класів, певні підформули - найважливіші дроби та ті, що створюються \left і \right - утворюють клас під назвою Inner, який явно доступний за допомогою команди \mathinner.

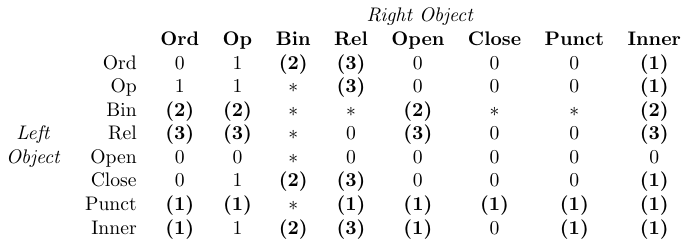
$Класи символів і інтервали$

У таблиці «0» означає «немає місця», «1» означає \thinmuspace, «2» означає \medmuskip, «3» означає \thickmuskip, «*» означає «неможливо». Записи, виділені жирним шрифтом, означають, що відповідний інтервал не додається в стилі математичних сценаріїв.

TeX обробляє інтервали у формулах, просто ідентифікуючи клас кожного об’єкта у формулі, а потім додаючи пробіл між кожною парою суміжних об’єктів, як визначено в попередній таблиці. Ця таблиця жорстко закодована в математичних процедурах набору тексту TeX, тому не може бути змінена пакетами макросів.

Двійковий символ перетворюється на Звичайний символ, якщо йому не передують і не слідують символи, сумісні з двійковою операцією. Тому деякі записи в таблиці позначені як неможливі. Наприклад, $+x$ дає +x (унарний плюс), а не + x. Останній може бути створений за допомогою ${}+x$ .

Розглянемо наступну формулу (значення за замовчуванням змінено, щоб чіткіше відображати додані пробіли):

1thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[
4a - b = -\max \{ x , y \}
5\]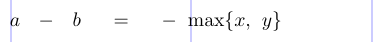

$\thinmuskip, \medmuskip і \thickmuskip$

TeX ідентифікує об’єкти як Ord, Bin, Ord і так далі, а потім вставляє пробіли наступним чином:

1 A      -      b      =      -    \max   \{   x    ,       y   \}
2Ord \: Bin \: Ord \; Rel \; Ord \, Op   Open Ord Punct \, Ord Close

Мінус перед \max перетворюється на Звичайний, оскільки Двійковий не може слідувати за Відношенням.

У конструкції “\left…\right" уся підформула, відмежована конструкцією, стає одним об’єктом класу *Inner*. Навпаки, такі команди, як \Biglі\Bigr створюють окремі символи класів *Opening* і *Closing* відповідно. Різниця між ними показана в таблиці інтервалів вище. Хоча вони можуть призвести до роздільників однакового вертикального розміру, відмінності між інтервалами можуть виникати залежно від суміжних об’єктів у формулі. Наприклад, *Ordinary*, за яким іде *Opening*, не отримує пробіл, тоді як *Ordinary*, за яким іде *Inner*, відокремлюється тонким пробілом. Пробіли всередині підформули в конструкції "\left…\right`” створені, як очікувалося, починаючи з символу Відкриття і закінчуючи символом Закриття.

1\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
2% -------------------------------------------------------------------------------
3\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]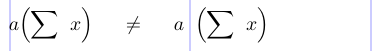

$\left…\right і \Bigl…\Bigr$

Таким чином, краще перевірити, чи символ належить до потрібного класу, а не просто шукати його в наступних таблицях.

9.2. Букви, цифри та інші Звичайні символи

Усі латинські літери ASCII без наголосу та арабські цифри називаються «алфавітними символами». Шрифт, яким вони набираються, може бути різним. У математичних формулах шрифт за замовчуванням для латинських літер — курсив, тоді як для арабських цифр — вертикальний/римський. Усі алфавітні символи належать до класу Ordinary.

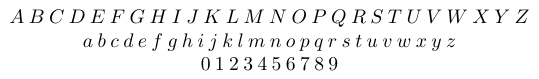
$Символи класу \mathord (грец.)$

На відміну від латинських літер, математичні грецькі літери більше не пов’язані з гліфами, які використовуються для набору звичайного грецького тексту. Через дивний випадок 18-го століття, у головній європейській традиції математичної типографіки шрифт за замовчуванням для малих грецьких літер у математичних формулах є курсивом, тоді як для великих грецьких літер він вертикальний/римський. (У фізиці та хімії, наприклад, типографські традиції дещо відрізняються.)

Великі грецькі літери в перших рядках наступної таблиці також є алфавітними символами, шрифт яких змінюється, за замовчуванням вертикальний/латинський. Існують великі грецькі літери, кожна з яких має такий самий вигляд, як латинська літера (наприклад, A і Alpha, B і Beta, K і Kappa, O і *Omicron *). Цих літер немає в таблиці. З цієї ж причини омікрон з маленької літери не існує. На практиці грецькі літери, схожі на латинські літери, не використовуються в математичних формулах.

$Грецькі літери$

Для синіх символів потрібен пакет amssymb. ^(var) вказує на змінний алфавітний символ.

У наступній таблиці наведено інші буквені символи класу Ordinary. Перші чотири — єврейські літери.

$Символи класу \mathord (у формі літери)$

Для синіх символів потрібен пакет amssymb.

У наступній таблиці наведено інші символи в класі Ordinary, включаючи деякі поширені знаки пунктуації. Вони поводяться як літери та цифри, тому навколо них ніколи не залишається додаткового місця.

$Символи класу \mathord (різне)$

Для символів синього кольору потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

Зверніть увагу, що знак оклику, крапка та знак питання не розглядаються як розділові знаки у формулах.

Синоніми: логічне заперечення - \lnot, \neg; | - \верт, |; || - \Vert, \|.

Поширеною помилкою є використання цих символів безпосередньо як бінарних операторів або символів відношення без використання правильно визначеної команди математичних символів для цього типу. Таким чином, якщо ви використовуєте такі команди, як \#, \квадрат або \&, уважно перевірте, чи ви отримали правильні міжсимвольні проміжки, або, навіть краще, визначте власну команду символу.

1\usepackage[fleqn]{amsmath} \usepackage{amssymb}
2\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
3\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
4% -------------------------------------------------------------------------------
5\[ a \neg b \qquad x \square y + z \]
6\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
7\[ a \bneg b \qquad x \rsquare y + z \]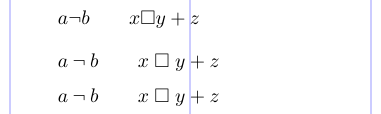

$Оголошення математичних символів$

Команда \DeclareMathSymbol використовується для оголошення імені вашого власного символу.

1\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}

Перший аргумент — це ім’я вибраної команди. Другий аргумент є однією з команд, що відповідає класу символів. Третій аргумент визначає шрифт символу, з якого символ має бути отриманий. Четвертий аргумент задає позицію символу в кодуванні шрифту: десяткове, вісімкове чи шістнадцяткове значення. Правильні значення для аргументів можна найпростіше знайти, переглянувши визначення у файлі amssymb.sty або fontmath.ltx (для основних символів). Наприклад, ми шукали \neq і \square, замінювали \mathord у кожному випадку та, нарешті, дали отриманому символу нову назву.

9.3. Математичні наголоси

У таблиці нижче наведено команди акцентів, доступні у формулах. Більшість із них визначені у стандартному TeX. Перегляньте тут інформацію про розширювані наголоси. Коли ви додаєте математичний акцент до символу, результатом є символ класу Ordinary.

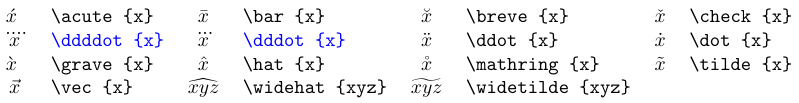
$Математичні акценти, надаючи підформули класу \mathord$

Акценти синього кольору вимагають пакета amsmath.

Останні два акценти доступні в діапазоні ширини, найбільший із яких використовується автоматично.

1\usepackage{amstext}
2% -------------------------------------------------------------------------------
3\[ a = b \text{ but } a \tilde{=} b
4\text{ which is not } a \mathrel{\tilde{=}} b \]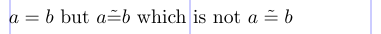

$Створення символу відношення із символу з наголосом$

Інші способи розміщення символів над символами Relation показано тут. Додаючи наголос до i або j в математичних формулах, найкраще використовувати безкрапкові варіанти \imath і \jmath.

9.4. Двійкові символи операторів

Існує понад 100 символів класу Binary, з яких можна вибрати. Більшість із них наведено в наступній таблиці. Деякі з них також доступні як символи Relation, хоча й під різними назвами.

$Символи класу \mathbin (різне)$

Для символів синього кольору потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

Лівий і правий трикутники також доступні як символи Відношення.

Пакет stmaryrd змінює Binary символи \bigtriangleup і \bigtriangledown на Operators, залишаючи лише синоніми \varbigtriangleup і \varbigtriangledown для Binary операторних форм.

Пакет amssymb пропонує декілька символів прямокутника для використання як Двійкових операторів; багато інших додано stmaryrd. Дивіться наступну таблицю.

$Символи класу \mathbin (коробки)$

Для всіх символів потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

Ви можете завантажити пакет stmaryrd з опцією heavycircles. У результаті кожна команда символу кола з наступної таблиці, яка починається з \var, замінює своє визначення відповідною командою без “var”; наприклад, символ \varodot стає \odot, і навпаки.

$Символи класу \mathbin (кружки)$

Для символів синього кольору потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

Параметр heavycircles пакета stmaryrd впливає на всі команди, що починаються з \var та їхні звичайні варіанти.

9.5. Символи відношення

Клас двійкових символів Relation навіть більший, ніж у Binary операторів. У наступній таблиці наведено символи рівності та порядку. Косу риску можна поставити через будь-який символ Відношення, поставивши перед ним команду \not. Заперечений символ представляє доповнення (або заперечення) відносин.

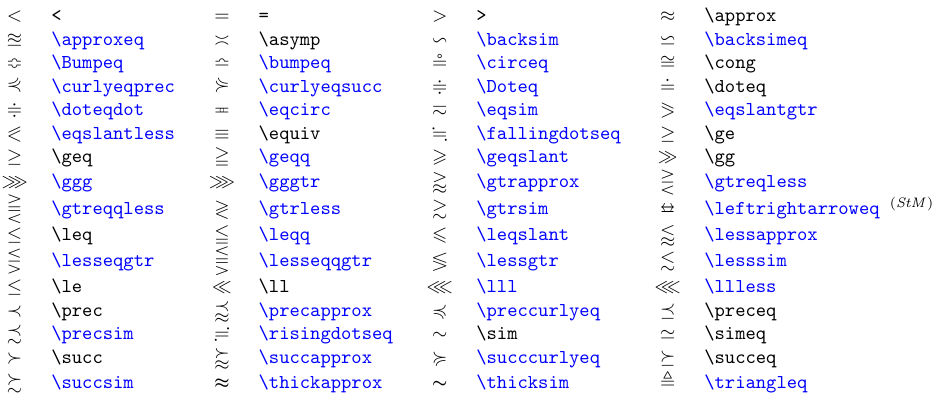
$Символи класу \mathrel (рівність і порядок)$

Для символів синього кольору потрібен або пакет amssymb, або, якщо позначено ^(StM), пакет stmaryrd.

1$ u \not< v$ or $a \not\in \mathbf{A} $

$Заперечення відношення$

Цей загальний метод заперечення символу Відношення не завжди дає хороші результати, особливо з більшими символами, тому що похила лінія завжди матиме той самий розмір, позицію та нахил. Через це також доступні деякі спеціально розроблені «заперечені символи». Перегляньте список у наступній таблиці.

$Символи класу \mathrel (рівність і порядок�заперечені)$

Для синіх символів потрібен пакет amssymb.

Якщо є вибір, зазвичай краще використовувати спеціально розроблені гліфи. Щоб зрозуміти чому, порівняйте символи в наступному прикладі.

1\usepackage{amssymb}
2% -------------------------------------------------------------------------------
3$ \not\leq \ \not\succeq \ \not\sim $ \par
4$ \nleq \ \nsucceq \ \nsim $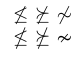

$Складені та спеціально розроблені символи запереченого відношення$

У наступній таблиці наведено символи Відношення для множин і включень.

$Символи класу \mathrel (множини та включення)$

Для символів синього кольору потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

А тепер заперечення символів Relation для множин і включення.

$Символи класу \mathrel (множини та заперечення включення)$

Для синіх символів потрібен пакет amssymb.

У наступній таблиці наведено символи Відношення у формі стрілок. Деякі розширювані конструкції стрілок, які створюють складені символи Relation, описані тут.

$Символи класу \mathrel (стрілки)$

Для символів синього кольору потрібен пакет amssymb або, якщо позначено ^(StM), пакет stmaryrd.

А ось заперечені символи Relation у формі стрілки.

$Символи класу \mathrel (відмінені стрілками)$

Для синіх символів потрібен пакет amssymb.

Існують інші елементи (крім \not, які використовуються для заперечення загальних символів Relation), які були спеціально розроблені для заперечення або розширення символів, схожих на стрілки. Дивіться наступну таблицю.

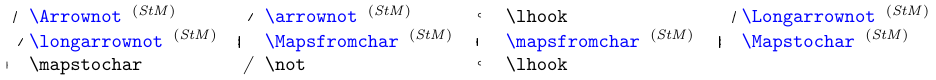
$Символи класу \mathrel (заперечення та розширення стрілок))$

Для синіх символів потрібен пакет stmaryrd.

Ці символи призначені для комбінування, переважно зі стрілками; наприклад, \longarrownot\longleftarrow.

Використовуйте \joinrel, щоб “склеїти” реляційні символи разом, наприклад, \lhook\joinrel\longrightarrow.

Розміри цих символів роблять їх непридатними для іншого використання.

1\usepackage{stmaryrd}
2% -------------------------------------------------------------------------------
3$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$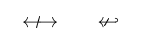

$Заперечення стрілок$

Нарешті, нижче наведено інші різноманітні символи Відношення.

$Символи класу \mathrel (різне)))$

Символи відношення синього кольору вимагають пакета amssymb.

\therefore є символом відношення, тому його інтервал може бути не таким, як очікується при звичайному використанні.

Шрифти в математичних формулах Математичні символи LaTeX та їхні супутники