7. 为布局进行调整

通常，乳胶在制定数学公式方面做得很好。但是有时需要对定位进行更好的调整。本文讨论了一些微调布局的技术，以使数学公式更好一些。

7.1. 自动尺寸和间距

当数学符号和字母出现在分数，下标或上文中时，通常会变小(并具有更紧密的间距)。数学公式可以以八种Tex数学样式进行布局：

D, D'	\displaystyle	单独显示在行上
T, T'	\textstyle	嵌入文本
S, S'	\scriptstyle	在上标或下标中
SS, SS'	\scriptscriptstyle	在所有高阶上标或下标中

文本样式 (T) 用于在连续文本中设置的公式的顶层（一对 $ 之间或 \( 和 \) 之间），显示样式用于在显示的公式的顶层（一对 $$ 之间或 \[ 和 \] 之间）。对于子公式，样式可从下表中确定：

D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

下一个示例说明了各种样式：

\normalsize                 %% Style:
\[ b                        %% D
    ^0                      %% S
   +                        %% D
   \frac{(k + p)            %% T
          _{j'}             %% S'
         % \displaystyle
         \pm                %% T [D]
         \frac{(f + q)      %% S [T]
                ^{(pk)      %% SS [S]
                   ^y       %% SS
                   _{j'}}}  %% SS'
              {(h + y)}}    %% S' [T']
        {(l + q)            %% T'
          ^{(pk)}}          %% S'
\]

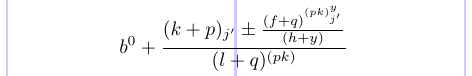
您可以在\displayStyle之前删除注释char(`’％’)，并查看一些样式如何更改为括号中的样式：

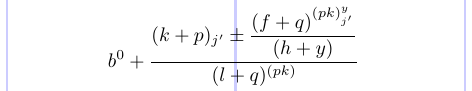
它显示了如何明确指定每个部分中要使用的样式。

7.2. 亚形成型

在文本中，一对牙套表示某些声明生效的组或范围。在数学公式中，它们另外，还划定了一个子形式，该子形式始终是添加到外部公式中的独立实体。结果，亚形式总是在其自然宽度上是排版的，当Tex构建试图将公式安装在线路中的段落时，不会水平伸展或收缩。我们已经表明，来自简单支撑组的子格式被处理好，就好像它是一个符号一样。这意味着一个空的组会产生一个可以改变间距的隐形符号。

下标/上标的内容以及许多（但并非所有）命令（例如 \frac 和 \mathrel）的参数也是子公式。因此，它们会得到相同的特殊处理。例如，\bm 的参数不一定设置为子公式，这是一个重要的例外。在数学公式中，如果只需要限制声明的范围，请使用 \begingroup 和 \endgroup 定义一个组。请记住，专门的数学声明（例如样式更改）会一直有效，直到当前子公式结束，无论是否存在任何其他组。

7.3. 大分界符

LaTeX 定义了四个命令 - \big、\Big、\bigg 和 Bigg - 用于直接控制可扩展分隔符的大小。它们接受一个参数（该参数必须是可扩展分隔符），并生成更大的分隔符版本，大小是基本分隔符大小的 1.2 到 3 倍。

这四个命令各自有三种变体，分别对应四种大小的开始符号（\bigl、\Bigl、\biggl 和 \Biggl）；四种大小的关系符号（\bigm、\Bigm、\biggm 和 \Biggm）；以及四种大小的结束符号（\bigr、\Bigr、\biggr 和 \Biggr）。所有这 16 个命令都必须与位于 \left、\right 或（使用 eTeX）\middle 之后的任何符号一起使用（请参阅此 表格）。

这些定系数的尺寸固定在标准乳胶中。但是，使用amsmath软件包，根据使用的字体大小和数学样式，尺寸适应周围材料的尺寸。这在下面的示例中显示。

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
\Large
\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]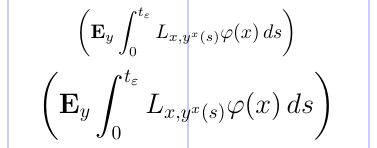

7.4. 调整自由基的索引

在标准 LaTeX 中，根号上的索引位置并不总是合适的。但是，您可以使用 amsmath 包中定义的命令 \leftroot 和 \uproot 来调整此索引的位置。这些命令的正整数参数分别将索引向左和向上移动，而负数参数则将索引向右和向下移动。这些参数以数学单位给出，非常小，因此这些命令适合进行微调。

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\[
  \sqrt[\beta]{k} \qquad
  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
\]

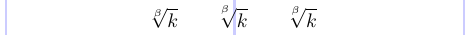
7.5. 用支柱和幻影进行微调

每当您想“完美”的排版数学间距和对齐方式时，通常最好转向原始Tex的独特和先进的能力。访问这些功能由与\phantom和\smash相关的许多命令提供。这些命令可以在数学公式或运行文本中使用。

让我们来看看以下示例：

\usepackage{amsmath}
\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
\newcommand\bfE{\mathbf{E}}
% -------------------------------------------------------------------------------
\begin{equation} \begin{split}
  f_{h, \ve}(x, y)
    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
    &\relphantom{=} {} + h \biggl[
       \frac{1}{\tve}
       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
    &\relphantom{=} \phantom{{} + h \biggl[ }
       \frac{1}{\tve}
       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
                                            \vf(x) \,ds    \biggr) \biggr]
\end{split} \end{equation}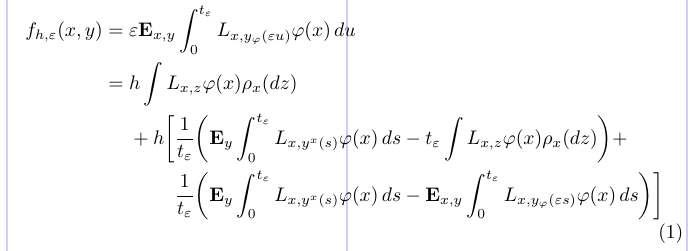

这里，\phantom 命令会调整水平位置。在序言中，它用于定义一个宽度与其参数（本例中为 =）相等的隐形关系符号。在数学环境中，它用于通过以“幻像”（即不可见的子公式）开头来对齐某些行。空括号 {} 与 \mathord{} 相同，后者会生成一个不可见的零宽度符号，用于获得正确的“+ h”间距（如果没有 {}，加号将生成一元加号，并在 h 之前出现不合适的间距）。

与 \phantom 不同，命令 \smash 会将其内容排版（在 LR 盒子中），但会忽略它们的高度和宽度，就好像它们都为零一样。标准 LaTeX 中定义的命令 \hphantom 是两者的组合。它生成的效果相当于 \smash{\phantom{some phantom contents}}，即一个高度和深度均为零、但宽度与幻像内容相同的不可见盒子。

\vphantom 命令类似，但它将幻像内容的宽度设为零，同时保留其总高度和深度。命令 \mathstrut 定义为 \vphantom(，生成一个高度和深度等于括号的零宽度盒子。

使用 amsmath 包，\smash 命令可以采用可选参数，这样 \smash[t]{...} 会忽略框内容的高度，保留深度，而 \smash[b]{...} 会忽略深度，保留高度。

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

似乎给 * y *用支柱额外的高度会使激进分子看起来相似。但是，相反，它只会使它们看起来更加不同，而且整体上更丑陋。事实证明，粉碎 * y *的底部是最好的方法。

以下示例显示了粉碎的非常普遍的用法。 \smash命令用于在那里提供对周围定界符高度的精细控制。这也表明，粉碎可能会引起问题，因为需要知道线的实际高度。这是由\ vphantom修复的。 \hmjd是定义为：

\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

为了显示由此产生的垂直空间，我们添加了规则：

Appearance	Code	Comment
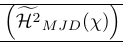	\left( {\Hmjd } \right)	外括号太大
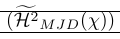	\left( \smash{\Hmjd } \right)	外括号太小，线太近
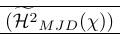	\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}	刚刚好！
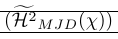	\left( \smash[t]{\Hmjd } \right)	需要 \vphantom 和部分 Smash

在一些地方，低级 TeX 处理的缺陷可能会导致排版细节出现错误。这种情况可能发生在特定的布局中，其中 (a) 子公式（分数的分子/分母或下标/上标）恰好由一个 LR 盒子或类似构造的数学盒子组成，并且 (b) 该盒子没有其自然大小，例如更复杂的 \makebox、smashes 和一些 phantoms 形式。

要看到这一点，让我们看看以下示例：

\[
\sqrt{ \frac{a+b}{x_j} } \quad
\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
\sqrt{ \frac{a+b}{\smash{x_j+b}} }
\]

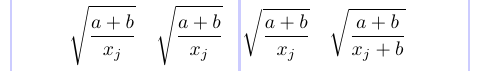
为了减少部首的深度，在第二个部首中添加了 \smash，但这没有效果。在第三个部首中，它与空括号组兼容。但在第四个部首中，不需要空括号组。总而言之，每当您发现 \smash 不起作用时，请尝试在单独的方框前添加一个空的数学子公式（{}），以确保其正确处理。

7.6. 水平间距

更精细，更困难的调整需要下表中显示的明确间距命令：

这些命令的完整形式和短形式都是可靠的，也可以在正常文本中使用数学公式以外。它们与20世纪中叶用于排版数学的机器上可用的薄，中和较厚的空间有关。

三个 TeX 参数 \thinmuskip、\medmuskip 和 \thickmuskip 的当前值定义了由 \..space 命令添加的空间量。它们与 amsmath 一起使用时的默认值列于表中。这些低级参数需要以数学单位 (mu) 为单位的值。因此，它们只能通过低级 TeX 赋值语句设置，而不能通过 \setlength 或类似的命令设置。此外，通常情况下，它们的值不应被修改，因为它们在 TeX 的数学排版过程中被内部使用（参见下表）。

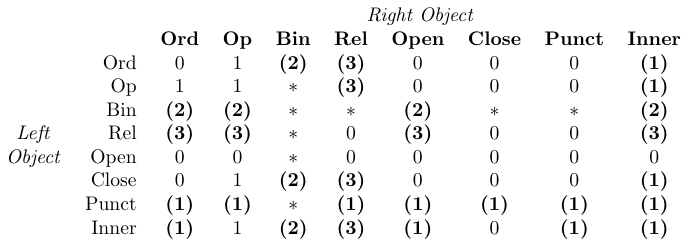
表中 0 表示“无空格”，1 表示 \thinmuspace，2 表示 \medmuskip，3 表示 \thickmuskip，* 表示“不可能”。粗体表示在数学脚本样式中不添加相应的空格。

一个数学单元(`1mu’)等于当前数学字体大小中的 em的1/18. 因此，A * Mu *的绝对值随数学样式而变化，无论使用哪种样式，都可以提供一致的间距。