8. 数学公式中的字体

LaTeX 字体简介

与普通文本不同，数学中通常不需要自动改变字体形状。不同的形状在数学中具有特定含义。例如，粗体正立字母可用于表示向量。如果公式中的字符因周围条件而改变形状，结果将是错误的。这就是数学公式中字体处理不同于正文的原因。

公式中的字符可以分为两类：符号和字母字符（包括数字）。实际上，TeX 内部处理八种类别来确定适当的间距。但在当前讨论中，划分为两类已经足够。

一些符号，例如 =，可以直接从键盘输入。然而，部分符号必须通过命令输入，例如 \leq 可得到“小于等于”符号。公式中的另一大类字符——字母字符——可以直接从键盘输入。

标准 LaTeX 预定义了超过 200 个符号，几乎可以排版任何所需的公式。这些符号分布在多个不同的字体中，但用户无需了解它们在内部的表示方式即可使用。如果需要，还可以以类似方式访问额外的符号字体。

符号和字母字符有一个对我们现在最重要的区别：在同一公式中，符号的图形表现是固定的，而用户可以改变字母字符的外观。改变公式中字母字符外观的命令被称为 数学字母标识符（math alphabet identifiers），与这些命令关联的字体称为 数学字母（math alphabets）。即使公式置于诸如默认斜体的定理环境中，也不会改变，因为字母标识符独立于公式外的字体命令。这一点非常重要，因为字符形状携带意义，必须在文档的任何出现处保持不变。

8.1. 数学字母标识符

仅仅一个字母表和大量符号对科学家来说远远不够。他们倾向于使用所有可用的字体来表示特殊概念。除了希腊字母等外文字母（通常作为符号访问——\alpha、\beta 等），我们还可以找到用于矩阵的无衬线字母、用于向量的粗体衬线字母、用于群、理想或域的 Fraktur 字体，甚至使用书法体来表示集合。约定的数量是无限的，并且在不同学科之间各不相同。LaTeX 正是通过允许声明新的数学字母标识符并将其关联到任意所需的字体形状组，来满足这种需求，而不是仅依赖于不可扩展的预定义集合。这些标识符是可在公式中使用的特殊命令，它们会把参数中的任何字母字符排版为特定的字体。正如我们稍后将在 此处看到的，在不同公式中可以使用不同的字体，但在同一公式中它们始终选择相同的字体，不受外部条件影响。

预定义字母标识符

LaTeX 已经内置了一些字母标识符。它们如下表所示。最后两行显示，公式中使用的字母来自数学字母 \mathnormal。另一方面，\mathit 产生的字母间距不同，这意味着该字母可以用于提供在某些学科中常见的完整单词变量名。

命令	示例代码	结果
\mathcal	$\mathcal{A}=a$
\mathrm	$\mathrm{max}_i$
\mathbf	$\sum x = \mathbf{v}$
\mathsf	$\mathsf{G}_1^2$
\mathtt	$\mathtt{W}(a)$
\mathnormal	$\mathnormal{abc}=abc$
\mathit	$differ\neq\mathit{differ}$

在 LaTeX2e 中，数学字母标识符是带有一个参数的命令，该参数可以是单个字母或单词，用特殊字体排版。

Therefore, $\mathsf{G}$ can be computed as
\begin{equation}
\mathsf{G} = \mathcal{A} +
             \sum_{i=1}^{n} \mathcal{B}_{i}
\end{equation}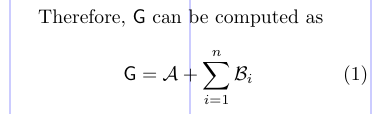

默认数学字母

如果没有显式指定字母标识符，字母字符默认从哪个字母集中选取？换句话说，默认的数学字母是什么？答案是：没有单一的默认数学字母。LaTeX 系统可以被设置为从不同的字母中提取字符，除非用户显式指定，否则通常会出现这种情况，如下面的示例所示。

\begin{eqnarray}
x &=& 12345 \\
\mathrm{x} &=& \mathrm{12345} \\
\mathnormal{x} &=& \mathnormal{12345}
\end{eqnarray}

从图中可以看到，\mathrm 不会改变数字，而 \mathnormal 不会改变字母。因此，在默认设置下，数字的默认字母是与 \mathrm 关联的数学字母，字母的默认字母是与 \mathnormal 关联的。这种行为可以通过 \DeclareMathSymbol 命令进行控制。

LaTeX 在数学中使用何种字体？

在 LaTeX 中，数学模式的默认字体通常是 Computer Modern。当然，也可以在文档导言区使用宏包指定其他字体。

自定义字母标识符

可以使用 \DeclareMathAlphabet 命令定义新的数学字母标识符。比如说，你想让斜体无衬线字体可作为数学字母使用。首先决定一个新命令名称，例如 \msfsl，作为字母标识符。然后参考下表找到合适的字体形状组。

例如，Computer Modern Sans 系列包含中等粗细的正立和斜体形状。如果你决定使用该系列的斜体形状，可以通过 \DeclareMathAlphabet 告诉 LaTeX。

\DeclareMathAlphabet{cmd}{encoding}{family}{series}{shape}

上述声明包含四个参数（标识符本身之外）：编码名称、字体族、粗细以及形状。下面的示例中，定义的字母标识符将始终切换为 Computer Modern Sans 中等斜体。

\DeclareMathAlphabet{\msfsl}{OT1}{cmss}{m}{sl}
% -------------------------------------------------------------------------------
We demonstrate this with the formula
\begin{equation}
\sum \msfsl{A}_{i} = a \tan \beta
\end{equation}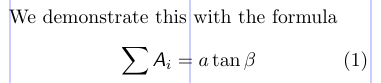

也可以在宏包文件或文档导言区重新定义已有的数学字母标识符。例如：

\DeclareMathAlphabet{\mathsf}{OT1}{pag}{m}{n}

这将覆盖 \mathsf 标识符的默认设置，使其在公式中使用 Adobe Avant Garde。

如果某个数学字母属于已经被 LaTeX 为其他目的加载的符号字体（例如 \mathcal），最好使用 \DeclareSymbolFontAlphabet，因为它更好地利用了 TeX 在数学方面相对有限的资源。

最佳数学字体

除默认的 Computer Modern 外，LaTeX 还内置了七种用于排版数学字母的字体，用户无需在导言区额外加载宏包即可自定义数学表达式。下面列出 8 种常用字体供你选择。

字体	用途	命令
正立罗马	标准正立字体	\mathrm{}
手写体	用于排版普通数学字母	\mathnormal{}
手写体（大写）	用于排版大写字母的特殊手写体	\mathcal{}
斜体字母	斜体文本	\mathit{}
正立 无衬线	正立无衬线字母	\mathsf{}
正立罗马粗体	正立罗马粗体字母	\mathbf{}
打字机体	正立打字机体字母	\mathtt{}

8.2. 数学中的文本字体命令

虽然像 \rmfamily 这样的文本字体声明不能在数学模式中使用，但诸如 \textrm 之类的字体切换命令可以在文本和数学中通用。使用这些命令，你可以在公式中临时切换到文本上下文，在公式中间排版逻辑上属于外部文本的一段文字。该文字的字体将取决于外围条件，即继承当前的编码、族、粗细和形状，示例如下：

\sffamily The result will be
\[ x = 10 \textbf{ and thus } y = 12 \]

从图中可以看到 Sans 家族被保留，粗细被改为粗体。由 amstext（同样由 amsmath 加载）提供的 \text 命令可能更有用。它会自动拾取当前的编码、族、粗细和形状，而不改变它们。

8.3. 数学公式版本

我们已经讨论了使用数学字母标识符改变公式部分外观的方式。LaTeX 还允许整体改变公式的外观。数学公式总是以某个 数学版本（math version）排版。你可以在数学模式之外使用 \mathversion 命令切换不同的数学版本，从而改变后续公式的整体布局。

LaTeX 默认提供两种数学版本：normal（普通）和 bold（粗体）。特殊宏包还能提供更多版本。例如，mathtime 宏包（用于商业 MathTime 字体）会设置一个名为 heavy 的数学版本，以使用 MathTime 字体的超粗符号排版公式。

显然，默认的数学版本是 \mathversion{normal}。粗体版本则会让字母字符和符号更粗，但大运算符（如 \sum）默认不会变化。下面的示例先以普通版本排版同一公式，再以粗体版本排版。

\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}
\mathversion{bold}
\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}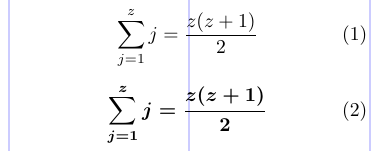

使用 \mathversion 可能适用于标题等特定情形，但需要注意改变版本会同时改变公式的外观乃至意义。如果只想加粗公式中的某些符号或字符，应该使用 \mathbf（针对字母）或 \bm（由 bm 宏包提供）而不是切换数学版本。

当切换数学版本时，LaTeX 会在内部表中查找该版本对应的所有符号位置。它可能也会更改数学字母标识符并将它们关联到该版本中的其他字体形状。

自定义的字母标识符（如前文示例中的 \msfsl）在所有数学版本中保持不变，只要它们是通过 \DeclareMathAlphabet 声明的。若要让某个字母标识符在特定数学版本中使用不同的字体，需要使用 \SetMathAlphabet 命令。例如，在默认设置下，\mathsf 标识符的定义如下：

\DeclareMathAlphabet{\mathsf}{OT1}{cmss}{m}{n}
\SetMathAlphabet{\mathsf}{bold}{OT1}{cmss}{bx}{n}

第一行在所有数学版本中将 Computer Modern Sans 中等斜体设为 \mathsf 的默认；第二行则指示 LaTeX 在粗体数学版本中使用 Computer Modern Sans 粗体扩展。

\SetMathAlphabet{cmd}{version}{encoding}{family}{series}{shape}

如前所述，\SetMathAlphabet 接受六个参数：字母标识符、目标数学版本以及四个用于定位字体的参数。

如果使用 \DeclareMathAlphabet 重新定义已有的字母标识符，所有先前针对该标识符的 \SetMathAlphabet 声明都会被清除。因此，除非再次添加新的 \SetMathAlphabet 声明，否则该标识符在所有数学版本中保持相同。

8.4. 使用 AMS‑LATEX 包调优公式字体

amsfonts（以及 amssymb）宏包定义了两个数学字母：欧拉 Fraktur 字母（\mathfrak）和黑板粗体字母（\mathbb）。示例：

\usepackage{amsfonts}
% -------------------------------------------------------------------------------
$ \forall n \in \mathbb{N} : \mathfrak{M}_n \leq \mathfrak{A} $

5. 粗体数学字体样式——bm 包

对于拉丁字母，仅使用 \mathbf 即可。对于其他字符，使用 bm 包更为合适。只需加载它并使用 \bm，即可让任意公式在可用的粗体字体范围内实现粗体效果。

下面的示例展示了多种使用 \bm 和 \mathbf 的方式，并演示了如何使用标准 LaTeX 的 \newcommand 与 bm 包提供的 \bmdefine 为常用粗体符号定义快捷命令。请注意，\mathbf{xy} 与 \bm{xy} 并不相同：前者产生粗体罗马 “xy”，后者产生粗体数学斜体 “xy”。

\usepackage{amsmath,amssymb,bm}
\newcommand\bfB{\mathbf{B}} \newcommand\bfx{\mathbf{x}}
\bmdefine\bpi{\pi} \bmdefine\binfty{\infty}
% -------------------------------------------------------------------------------
\section{The bold equivalence
  $\sum_{j < B} \prod_\lambda : \bm{\sum_{x_j} \prod_\lambda}$}
\begin{gather}
  B_\infty + \pi B_1 \sim \bfB_{\binfty} \bm{+} \bpi \bfB_{\bm{1}}
    \bm {\sim B_\infty + \pi B_1}\\
  B_\binfty + \bpi B_{\bm{1}} \bm{\in} \bm{\biggl\lbrace}
    (\bfB, \bfx) : \frac {\partial \bfB}{\partial\bfx}
    \bm{\lnapprox} \bm{1} \bm{\biggr\rbrace}
\end{gather}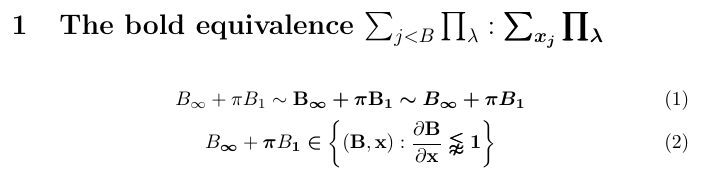

本例中 bm 尽力满足对各个符号和字母的粗体需求。但细观察会发现，结果并非总是最优的。例如，求和与乘积运算符采用了“穷举式粗体”（poor man’s bold）技术，即将符号重叠打印三次以产生粗体效果；而大括号根本没有加粗。由于 Computer Modern 数学字体并非所有符号都有粗体变体，这类缺陷无法完全避免。

bm 实际遵循的规则是什么？总体而言，它利用 LaTeX 已包含的 粗体 数学版本（通过 \boldmath 访问）来排版整个公式的粗体。如果某个符号在粗体版本中对应的字体与普通版本不同，bm 会直接使用该粗体字体，从而得到完美的结果（前提是粗体版本已正确配置）。如果两者相同，则假设没有可用的粗体变体，进而使用穷举式粗体。

请在修改现有数学字体设置的宏包之后再加载 bm 包！

对分隔符（如示例中的 \biggl\lbrace）的处理更加复杂。TeX 通常根据请求的高度在一系列不同尺寸的字形中选取合适的分隔符。这些字形可能位于不同的字体中，且某些尺寸可能没有粗体变体。因此，bm 只能根据粗体数学版本提供的字体来排版分隔符。在 Computer Modern 中，仅最小尺寸的分隔符提供了粗体，其余尺寸只能使用普通字体。

\usepackage{bm}
% -------------------------------------------------------------------------------
$\bm{\Biggl\lbrace\biggl\lbrace\Bigl\lbrace\bigl \lbrace \lbrace
  \mathcal{Q}
  \rangle \bigr\rangle\Bigr\rangle\biggr\rangle
\Biggr\rangle}$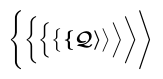

通常，如果一个接受参数的命令出现在 \bm 的参数内部，则该命令必须完整包含在 \bm 的参数中。这样，所有排版内容都将加粗。如果只想让命令的输出部分加粗，需要把不需要加粗的符号放在 \mbox 中，并在盒子内容内部使用 \unboldmath 显式恢复普通数学版本。\mbox 在 TeX 中被视为 普通（Ordinary）类符号，因此为保证间距正确，可能需要在其前后加上 \mathbin、\mathrel 或 \mathop。

\usepackage{amsmath,bm}
% -------------------------------------------------------------------------------
$ \bm{\sqrt[2]{x \times \alpha}} $ but
$ \bm{\sqrt[2]{x \mathbin{\mbox{\unboldmath$\times$}} \alpha}} $
or the similar
$ \bm{\sqrtsign}{\bm{x} \times \bm{\alpha}} $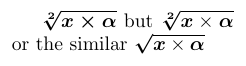

幸运的是，这类复杂操作并不常见。多数情况下，仅需在参数的某些部分加粗即可，这可以通过在这些部分内部使用 \bm 来实现。正如前例中的 \sqrtsign，对于常见的粗体重音符，\bm 已专门编程以允许重音的参数位于自身参数之外。但如果你经常需要为此类重音创建快捷方式，最好自行定义，例如：

提升性能

虽然 \bmdefine\bpi{\pi} 看似仅是 \newcommand\bpi{\bm{\pi}} 的简写，实际上它的工作方式几乎相反：\bmdefine 会先创建一个隐藏的临时命令，然后立即使用该临时命令生成粗体符号。换言之，每次调用 \bm{\alpha} 时都会重新执行一次 \bmdefine，这相当耗时。如果在导言区提前定义 \bmdefine\balpha{\alpha}，则以后使用 \balpha 时只会调用一次已完成的工作。

\usepackage{bm}
\bmdefine\bhat{\hat}
% -------------------------------------------------------------------------------
$\hat a \neq \bm{\hat a} \neq \bm\hat a = \bhat a\neq \bm\widehat a$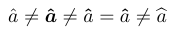

该示例还表明，变量宽度的重音（例如 \widehat）与分隔符共享同一缺陷：在 Computer Modern 数学设置中，它们来源于没有粗体变体的字体。