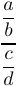5. 分数、二项式系数和数学样式
在数学公式中,你经常会看到分数以及其他类似的结构,比如分子放在分母之上。后者的一个例子是二项式系数。
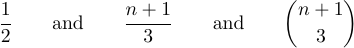
你可以通过输入 $1\over2$、$n+1\over3$ 和 $\n+1\choose3$ 来得到这三个以显示公式形式呈现的式子。
\over 命令会作用于公式中的所有内容,除非你用大括号将其包裹在一个特定的子公式中,在这种情况下,\over 只作用于该子公式内部。

在同一个子公式中不能使用两次 \over,例如,a\over b\over 2 是不合法的。相反,你应该显式指定分子和分母:

看起来两个公式都不是很美观。在这种情况下,通常最好把分数转换为“斜杠形式”。例如,最后两个公式应当这样书写:
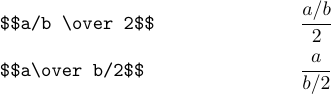
下面是更复杂的例子:
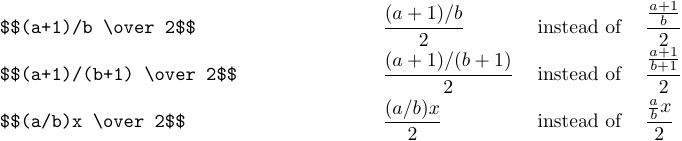
从上面的例子可以看到,当字母和其他符号出现在分数中时,它们有时会变小,就像它们出现在下标或上标时一样。现在我们来讨论 TeX 如何选择符号大小。TeX 有八种样式可以用于排版公式:
- display style(用于单独一行显示的公式)
- text style(用于嵌入正文的公式)
- script style(用于作为上标或下标的子公式)
- scriptscript style(用于二级上标或下标的子公式)
以及四种“紧凑”样式,除了上标和下标的提升程度更小之外,基本相同。我们将这八种样式分别记作 D、D’、T、T’、S、S’、SS、SS’,其中 D 为 display style,D’ 为紧凑的 display style,T 为 text style,依此类推。TeX 还使用三种字号来排版数学公式:正文大小、脚本大小和脚本脚本大小。
要在正文中排版公式,只需用 $... 将其包裹,例如:
(此处会产生 T 样式的公式)。或者你可以使用 $...$ 来得到一个显示公式;这会以 D 样式显示公式。公式的子公式可以采用不同的样式。一旦你知道了样式,就可以确定 TeX 将使用的字号:

没有 “SSS” 样式,因为如此微小的符号几乎不可读。

例如,如果 x^{a_b} 需要以 D 样式排版,则 a_b 将以 S 样式显示,b 将以 SS 样式显示;结果如下:
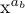
我们尚未看到 D 与 T 样式之间的区别。实际上,两者在指数的位置上有细微差别,尽管两者都使用脚本大小。但在处理分数时,D 与 T 样式之间的区别非常明显:

因此,如果在正文中输入 $1\over2,你会得到 S 样式在 S’ 上方的效果。但如果在显示公式中输入 $1\over2$,则会得到 T 样式在 T’ 上方的效果。
最后,\underline 不会改变样式。数学重音、\sqrt 和 \overline 命令会把非紧凑样式转换为对应的紧凑样式,同时保持紧凑。
有时你可能不喜欢 TeX 按其默认规则选择的样式。你可以通过输入 \displaystyle、\textstyle、\scriptstyle 或 \scriptscriptstyle 来显式指定所需的样式;所选样式会一直作用到公式或子公式结束,或直到你再次指定另一种样式。例如,$n+\scriptstyle n+\scriptscriptstyle n.$ 将产生如下显示:
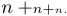
可以看到,随着样式的变化,加号也会变小,并且在脚本样式中 TeX 不会在 + 周围添加空格。
我们来看另一个例子——连续分数。
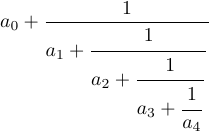
你可以这样输入:
1$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$如果在此公式中省略 \strut 和 \displaystyle,结果会不同:
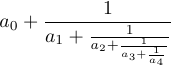
LaTeX 定义了宏 \frac,允许你使用另一种语法来指定分数:\frac{a}{b} 等价于 a\over b,\frac12 等价于 1\over2。
还有另一个操作 \atop,它类似于 \over,但不会绘制分数线:

LaTeX 还定义了 \choose,其作用类似于 \atop,但会把结果用括号括起来:
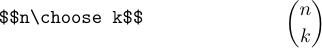
之所以称为 \choose,是因为它是二项式系数的常用记号,用来表示从 n 个元素中选取 k 个的方式数。
\over、\atop 和 \choose 这三个命令不能混用。例如,$n\choose k\over 2$ 是非法的。你必须使用分组来得到合法的形式:${n\choose k}\over2$ 或 $n\choose{k\over2}$。
TeX 还有 \above 命令,它是 \over 和 \atop 的通用版本。使用该命令时,你可以通过 \above<dimen> 来指定线条的确切粗细。例如:
1$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$将会产生一个复合分数,分子和分母之间的分数线厚度为 1pt: