10. 最受欢迎的 LaTeX 数学符号及其伴随

最受欢迎的 LaTeX 数学符号

在数学公式中经常使用的关键符号之一是求和符号。在接下来的章节中，我们将探讨在 LaTeX 中使用和格式化求和符号的方法。

求和符号以希腊字母 Sigma 表示，用于表示一系列项的相加。它使数学家能够简洁地表达诸如求和、数列和级数等概念。在 LaTeX 中，求和符号可以通过特定命令轻松地嵌入数学表达式中。

要在 LaTeX 中使用求和符号，需要使用命令 \sum。其通用语法如下：

1\sum_{i=lower}^{upper} expression

此处，变量 i 表示求和的索引。下限和上限定义了求和的范围。表达式可以包含数学项，表示要被求和的内容。

例如，要表示从 1 到 5 的数字之和，LaTeX 代码如下：

1$\sum_{i=1}^{5} i$

它将产生如下输出：

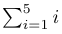
$一个简单的求和符号示例$

另一个经常使用的 LaTeX 数学符号是 LaTeX 极限符号。下面，我们将深入探讨它在数学公式中的意义和用法。

LaTeX 极限符号通常表示为 lim，是用于描述函数在趋近特定值或无穷大时行为的基本数学符号。通过了解与此符号相关的 LaTeX 命令，用户可以在数学表达式中准确地表示极限。

要在 LaTeX 中生成极限符号，只需使用命令 \lim，后跟任何需要的额外说明。例如，输入

1$\lim_{x \to \infty}f(x)$

将产生极限符号，变量 x 趋向无穷大的形式如下：

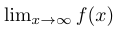
$一个简单的极限示例$

此符号有效地传达了当输入变量趋向无限大时，函数行为的观察。

在数学公式中，LaTeX 极限符号在表达函数的行为和边界方面起着关键作用。它使研究人员、教育工作者和学生能够准确描述和分析诸如收敛、连续性和可微性等数学概念。

此外，LaTeX 极限符号可以与其他符号和运算符结合，构建更复杂的数学表达式。例如，将极限符号与求和符号结合使用，允许用户表示具有可变上下限的求和。这种灵活性和多功能性使 LaTeX 成为数学排版的宝贵工具。

LaTeX 中的符号极限允许用户定义数学表达式的边界或约束。它们对于准确表示如求和、积分和乘积等运算的概念至关重要。通过使用适当的 LaTeX 命令，用户可以在符号上定位极限，以指定数学运算的范围或行为。

为了说明 LaTeX 中的符号极限，下面以求和符号为例。求和符号常用于表达一系列项的总和。使用 \sum 命令，用户可以生成求和符号。然而，要定义求和的上下限，需要使用额外的命令。

例如，输入

1$\sum_{i=1}^n$

将把下标定位为 i=1，上标为 n。此表示法表明求和操作应在 i 从 1 开始到 n 结束的范围内进行。

除了默认位置外，LaTeX 还允许用户自定义极限的位置。使用 \limits 命令，用户可以将极限置于求和符号的上方和下方。例如，输入

1$\sum\limits_{i=1}^n$

将把极限置于求和符号的上下方，提供更清晰的表示。这也是显示模式下的默认行为。因此

1$\sum{i=1}^n$

不需要 \limits。但若要切换回索引位置的极限，需要使用 \nolimits。

比较下表中的变体：

$不同位置和模式下的符号极限$

本节我们将探讨如何使用 relsize 宏包在 LaTeX 中获取更大的求和符号。借助 relsize 宏包，用户可以轻松调整数学符号的大小，包括求和符号，以满足特定需求。

首先，用户需要在 LaTeX 文档的导言区加入以下行以引入 relsize 宏包：

1\usepackage{relsize}

宏包引入后，用户可以使用 \mathlarger{} 命令获得更大的求和符号。将所需的表达式放入 \mathlarger{} 的大括号中，求和符号将以更大的尺寸显示。

考虑以下示例：

1\begin{equation*}
2\sin x = \mathlarger{\mathlarger{\sum}}_{n=0}^{\infty}(-1)^n\frac{x^{2n + 1}}{(2n + 1)!}
3\end{equation*}

它将在下面产生如下输出：

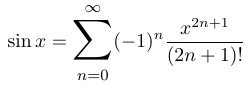
$大的求和符号$

正如我们所见，LaTeX 的 relsize 宏包提供了一种便捷方式来获取更大的求和符号。通过在文档导言区引入该宏包并使用 \mathlarger{} 命令，用户可以根据具体需求调整求和符号的大小。