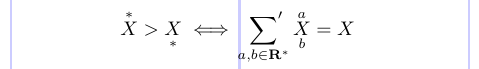4. Verzierte Symbole und zusammengesetzte Strukturen | LaTeX

Das Paket amsmath bietet einige Befehle zum Erstellen von Strukturen wie bruchähnlichen Objekten und dekorierten Symbolen. Hier werden einige davon besprochen.

4.1. Allgemeine Brüche

Das Paket amsmath definiert den Befehl \genfrac, der einen verallgemeinerten Bruch erzeugt.

1\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Die ersten beiden Argumente definieren linke bzw. rechte Trennzeichen. Mit dem dritten Argument thick können Sie die Standarddicke der Bruchregel überschreiben. Binominalkoeffizienten (siehe unten) verwenden beispielsweise den Wert 0pt für dieses Argument, um die Linie unsichtbar zu machen. Der Standardwert (wenn leer gelassen) der Linienstärke wird durch die aktuelle Schriftarteinstellung für den mathematischen Schriftsatz bestimmt. Die folgende Liste enthält die in den Beispielen dieses Artikels verwendeten Standardwerte.

Style	Default Thickness
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

Das vierte Argument, style, überschreibt (sofern es nicht leer gelassen wird) den mathematischen Stil für das verwendete Layout und die verwendete Schriftgröße. Der Wert muss im Bereich 0-3 liegen: 0 – \displaystyle, 1 – \textstyle, 2 – \scriptstyle, 3 – \scriptscriptstyle. Wenn dieses Argument leer bleibt, wird der Stil gemäß den normalen Regeln für Brüche ausgewählt. Die letzten beiden Argumente sind Zähler und Nenner.

Die alten Bruchbefehle \over, \overwithdelims, \atop, \atopwithdelims, \above und \abovewithdelims, die Standard-LaTeX von TeX erbt, erzeugen Warnungen, wenn sie mit dem Paket amsmath verwendet werden.

4.1.1. Einfache Brüche

Mit dem Befehl \genfrac definiert das Paket amsmath außerdem drei Befehle als praktische Abkürzungen: \frac, \dfrac und \tfrac.

1\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
2\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
3\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

Das folgende Beispiel zeigt die Verwendung dieser Befehle:

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \frac{1}{k} \log_2 c(f)
5  \quad \tfrac{1}{k} \log_2 c(f)
6\end{equation}
7Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
8        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.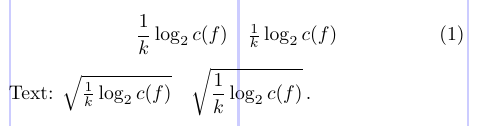

$\frac, \dfrac und \tfrac$

4.1.2. Binomialkoeffizienten

Eine weitere bruchartige Struktur sind Binomialkoeffizienten. Um Ihnen beim Schreiben zu helfen, bietet das Paket amsmath ähnliche Befehle \binom, \dbinom und \tbinom.

So wird der Befehl \genfrac abgekürzt:

1\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
2\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
3\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

Und hier ist das Beispiel:

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
5\end{equation}
6Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.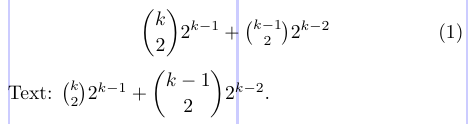

$\binom, \dbinom und \tbinom$

4.1.3. Fortsetzungsbrüche

Wenn Sie ein Brucharray setzen müssen, das im Wesentlichen ein unendlicher Bruch ist, der auch als „Fortsetzungsbruch“ bezeichnet wird, gibt es den Befehl \cfrac im Paket amsmath. Übergeben Sie das optionale Argument [l] oder [r], um einen Zähler links oder rechts auszurichten, der standardmäßig zentriert ist.

 1\usepackage{amsmath}
 2% -------------------------------------------------------------------------------
 3\begin{equation*}
 4\cfrac {1}{\sqrt{2} +
 5  \cfrac {1}{\sqrt{3} +
 6    \cfrac {1}{\sqrt{4} +
 7      \cfrac[r] {1}{\sqrt{5} +
 8        \cfrac[l] {1}{\sqrt{6} + \dotsb }
 9}}}}
10\end{equation*}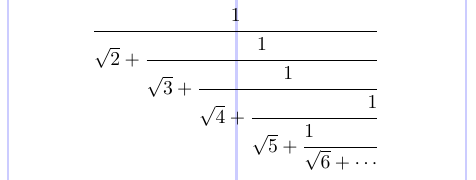

$Ein Kettenbruch$

4.2. Box-Mathematik

Das Paket amsmath stellt den Befehl „\boxed“ ähnlich wie \fbox bereit, um den Inhalt des Mathematikmodus in eine Box zu packen.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
5\end{equation}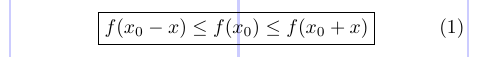

$Eine Boxformel$

4.3. Grenzen setzen

Tiefgestellte und hochgestellte Zeichen für Integrale, Summen, Produkte oder andere Operatoren können entweder über und unter dem mathematischen Operator (der „Grenzposition“) oder an der tiefgestellten/hochgestellten Position rechts vom Operator platziert werden. Normalerweise werden im Text keine Begrenzungen verwendet (andernfalls können sich die Zeilen ausbreiten). In einer angezeigten Formel hängt die Platzierung vom Operator ab. Das folgende Beispiel zeigt die Standardplatzierung in LaTeX.

1\[
2\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
3\]
4Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.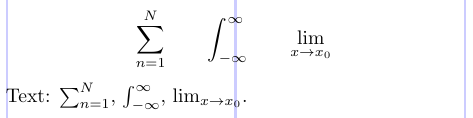

$Die Standardplatzierung der tiefgestellten/hochgestellten Zeichen in LaTeX$

Das Paket amsmath bietet Optionen zur Steuerung der Positionierung. Sie sind unten aufgeführt, wobei default das Verhalten markiert, falls das Paket amsmath mit einer Standard-LaTeX-Dokumentklasse, aber ohne eine dieser Optionen verwendet wird.


`intlimits`, `nointlimits`	Platziert hochgestellte/tiefgestellte Zeichen der Integrationssymbole jeweils oberhalb und unterhalb bzw. seitlich (Standard). Wird nur in angezeigten Formeln verwendet.
`sumlimits`, `nosumlimits`	Platziert hochgestellte/tiefgestellte Zeichen von großen Operatoren (Summe, Produkt usw.) jeweils oberhalb und unterhalb (Standard) bzw. seitlich. Wird nur in angezeigten Formeln verwendet.
`namelimits`, `nonamelimits`	Ähnlich wie `sumlimits` oder `nosumlimits`, aber für bestimmte Operatoren oder „Operatornamen“ wie `inf`, `sup`, `lim`, `min`, `max`, die traditionell mit tiefgestellten Zeichen darunter gesetzt werden, zumindest wenn sie in einer angezeigten Formel vorkommen.

TeX verfügt über drei primitive Befehle, die unmittelbar nach dem Symbol- oder Operatornamen erscheinen und die Positionierung von tiefgestellten/hochgestellten Zeichen steuern: \limits, \nolimits und \displaylimits. Der Befehl \displaylimits erzeugt tiefgestellte/hochgestellte Zeichen an der Grenzposition, wenn der aktuelle Mathematikstil ein Anzeigestil ist. Dies ist das Standardverhalten, wenn ein Symbol der Klasse Operator erscheint oder ein \mathop-Befehl verwendet wird. Wenn Sie einen Operator mit tiefgestellten/hochgestellten Zeichen an der Grenzposition außerhalb einer Anzeige setzen müssen, müssen Sie ihn einzeln mit dem Befehl \limits deklarieren.

Vergleichen Sie das folgende Beispiel mit dem vorherigen.

1\[
2\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
3\]
4Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.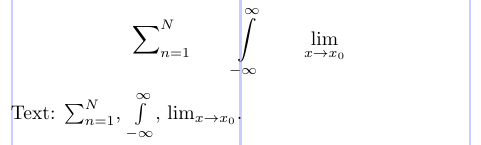

$Steuern der Platzierung der tiefgestellten/hochgestellten Zeichen mit TeX-Primitiven$

4.3. Mehrere Integrale

Um mehrere Integralzeichen mit gut angepassten Abständen dazwischen sowohl im Text als auch in der Anzeige zu setzen, verwenden Sie die Befehle \iint, \iiint und \iiiint. \idotsint erzeugt zwei Integralzeichen mit Auslassungspunkten dazwischen.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{gather*}
4\iint \limits _V f(x,y) \,dx \,dy \\
5\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
6\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
7\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
8\end{gather*}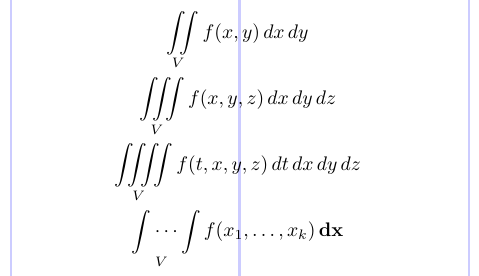

$Mehrere Integrale$

4.4. Modulare Beziehungen

Die mod-Notation für Äquivalenzklassen ganzer Zahlen unterliegt den speziellen Abstandskonventionen. Um damit umzugehen, bietet das Paket amsmath die Befehle \mod, \bmod, \pmod und \pod. Das folgende Beispiel zeigt die Verwendung dieser Befehle.

 1\usepackage{amsmath}
 2% -------------------------------------------------------------------------------
 3\begin{align*}
 4u & \equiv v + 1 \mod{n^2} \\
 5u & \equiv v + 1 \bmod{n^2} \\
 6u & = v + 1 \pmod{n^2} \\
 7u & = v + 1 \pod{n^2}
 8\end{align*}
 9The in-text layout: $ u = v + 1 \pmod{n^2} $
10\begin{gather*}
11(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
12x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
13\end{gather*}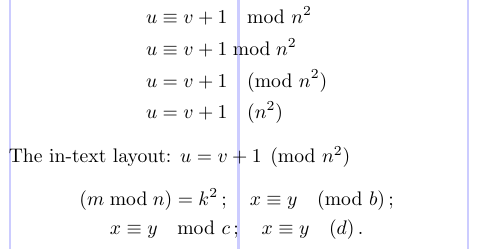

$Modulare Beziehung$

Mit amsmath wird der Abstand von \pmod innerhalb einer nicht angezeigten Formel verringert.

4.5. Mathematische Punktakzente

Zusätzlich zu den mathematischen Akzenten \dot und \ddot stellt das Paket amsmath die Befehle \dddot und \ddddot bereit, die dreifache bzw. vierfache Punktakzente erzeugen.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

$Punktakzente$

4.6. Hochgestellte Zeichen aus Akzenten machen: das Paket `amsxtra`.

Das Paket amsxtra bietet eine nützliche Funktion, eine Sammlung einfacher Befehle zum Platzieren von Akzenten als hochgestellte Zeichen für Unterformeln:

1\usepackage{amsxtra}
2% -------------------------------------------------------------------------------
3$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
4$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
5$(abc)\sphat$ \quad $(abc)\sptilde$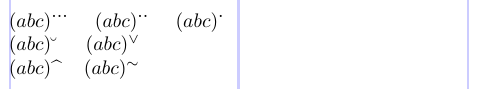

$Akzente als hochgestellte Zeichen$

4.7. Andere Dekorationen

Standard-LaTeX verfügt über den Befehl \stackrel, der einen hochgestellten Index über einem Relation-Symbol platziert. Darüber hinaus definiert das Paket amsmath die Befehle \overset und \underset. Verwenden Sie es, um Material über oder unter einem Ordinary- oder Relation-Symbol oder einem Binary-Operator-Symbol zu platzieren.

Der Befehl \sideset fügt zusätzlich zu den normalen Grenzwerten Dekorationen zu jedem Operator-Symbol (Summe, Produkt usw.) hinzu. Diese werden an den tiefgestellten und hochgestellten Positionen links und rechts vom Operator platziert.

1\[ \overset{*}{X} > \underset{*}{X}
2\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
3\overset{a}{\underset{b}{X}} = X \]

$Mehr Dekoration$