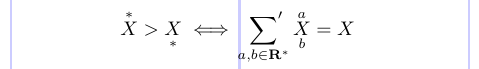4. Símbolos decorados y estructuras compuestas | LaTeX

El paquete amsmath proporciona algunos comandos para producir estructuras como objetos con forma de fracciones y símbolos decorados. Este análisis cubre algunos de ellos.

4.1. fracciones generales

El paquete amsmath define el comando \genfrac, que produce una fracción generalizada.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Los dos primeros argumentos definen los delimitadores izquierdo y derecho, respectivamente. Usando el tercer argumento, grueso, puedes anular el espesor predeterminado de la regla de fracción. Por ejemplo, los coeficientes binomiales (ver más abajo) usan el valor “0pt” para este argumento para hacer que la línea sea invisible. El valor predeterminado (cuando se deja vacío) del grosor de la línea lo determina la configuración de fuente actual para la composición tipográfica matemática. La siguiente lista contiene los valores predeterminados utilizados en los ejemplos de este artículo.

Estilo	Grosor predeterminado
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

El cuarto argumento, estilo, anula (si no se deja vacío) el estilo matemático para el diseño y el tamaño de fuente utilizado. El valor debe estar en el rango 0-3: 0 - \displaystyle, 1 - \textstyle, 2 - \scriptstyle, 3 - \scriptscriptstyle. Si este argumento se deja vacío, el estilo se selecciona según las reglas normales para fracciones. Los dos últimos argumentos son el numerador y el denominador.

Los antiguos comandos de fracción \over, \overwithdelims, \atop, \atopwithdelims, \above y \abovewithdelims, que LaTeX estándar hereda de TeX, producen advertencias cuando se utilizan con el paquete amsmath.

4.1.1. fracciones simples

Al tener el comando \genfrac, el paquete \amsmath también define tres comandos como abreviaturas convenientes: \frac, \dfrac y \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

El siguiente ejemplo demuestra el uso de estos comandos:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.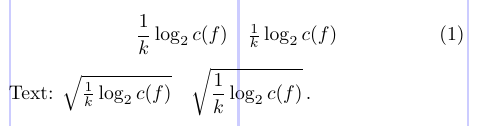

4.1.2. Coeficientes binomiales

Otra estructura similar a una fracción son los coeficientes binomiales. Para ayudarle a componerlos, el paquete amsmath proporciona comandos similares \binom, \dbinom y \tbinom.

Así abrevian el comando \genfrac:

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

Y aquí está el ejemplo:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.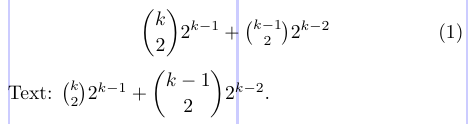

4.1.3. fracciones continuas

Si necesita componer una matriz de fracciones, que es esencialmente una fracción infinita, también conocida como “fracción continua”, existe el comando \cfrac en el paquete amsmath. Pase el argumento opcional [l] o [r] para alinear un numerador a la izquierda o a la derecha, que está centrado de forma predeterminada.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}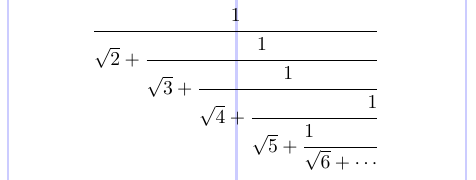

4.2. Matemáticas en caja

El paquete amsmath proporciona el comando \boxed similar a \fbox para colocar el contenido del modo matemático en un cuadro.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}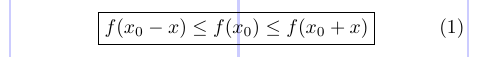

4.3. Posicionando los límites

Los subíndices y superíndices de integrales, sumas, productos u otros operadores se pueden colocar encima y debajo del operador matemático (la “posición límite”) o en la posición de subíndice/superíndice a la derecha del operador. Normalmente, los límites no se utilizan en el texto (de lo contrario, las líneas pueden extenderse). En una fórmula mostrada, la ubicación depende del operador. El siguiente ejemplo muestra la ubicación predeterminada en LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.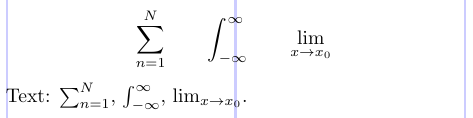

El paquete amsmath ofrece opciones para controlar el posicionamiento. Se enumeran a continuación, donde default marca el comportamiento en caso de que el paquete amsmath se use con una clase de documento LaTeX estándar pero sin ninguna de estas opciones.

intlimits, nointlimits	Coloca los superíndices/subíndices de los símbolos de integración arriba y abajo o al costado (predeterminado), respectivamente. Se utilizan solo en fórmulas mostradas.
sumlimits, nosumlimits	Coloca los superíndices/subíndices de operadores grandes (suma, producto, etc.) arriba y abajo (predeterminado) o al costado, respectivamente. Se utilizan solo en fórmulas mostradas.
namelimits, nonamelimits	Similar a sumlimits o nosumlimits pero para ciertos operadores, o “nombres de operadores”, como inf, sup, lim, min, max, que tradicionalmente se escriben con subíndices debajo, al menos cuando aparecen en una fórmula mostrada.

TeX tiene tres comandos primitivos que, aparecidos inmediatamente después del símbolo o nombre del operador, controlan la posición de los subíndices/superíndices: \limits, \nolimits y \displaylimits. El comando \displaylimits produce subíndices/superíndices en la posición límite cuando el estilo matemático actual es un estilo de visualización. Este es el comportamiento predeterminado siempre que aparece un símbolo de clase Operador o se utiliza un comando \mathop. Si necesita componer un operador con subíndices/superíndices en la posición límite fuera de una pantalla, debe declararlo individualmente usando el comando \limits.

Compare el siguiente ejemplo con el anterior.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.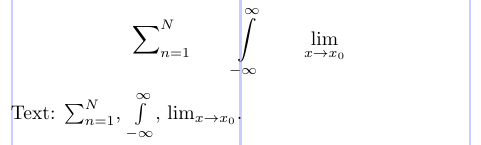

4.3. Integrales múltiples

Para componer múltiples signos integrales con espacios bien ajustados entre ellos tanto en texto como en pantalla, use los comandos \iint, \iiint y \iiiint. El \idotsint produce dos signos integrales con puntos suspensivos entre ellos.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}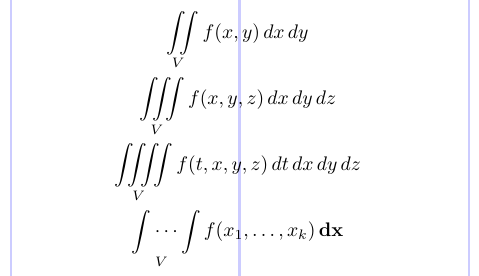

4.4. Relaciones modulares

La notación “mod” para clases de equivalencia de números enteros se rige por convenciones de espaciado especiales. Para solucionarlo, el paquete \amsmath ofrece los comandos \mod, \bmod, \pmod y \pod. El siguiente ejemplo muestra el uso de estos comandos.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}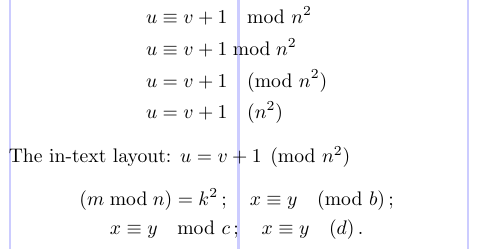

Con amsmath, se reduce el espaciado de \pmod dentro de una fórmula no mostrada.

4.5. Acentos de puntos matemáticos

Además de los acentos matemáticos \dot y \ddot, el paquete amsmath proporciona los comandos \dddot y \ddddot, que producen acentos de puntos triples y cuádruples, respectivamente.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Crear superíndices a partir de acentos: el paquete amsxtra

El paquete amsxtra ofrece una característica útil, una colección de comandos simples para colocar acentos como superíndices en subfórmulas:

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$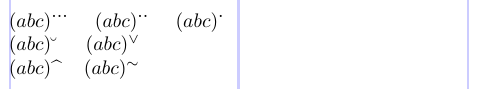

4.7. Otras decoraciones

LaTeX estándar tiene el comando \stackrel que coloca un superíndice encima de un símbolo Relación. Además, el paquete amsmath define los comandos \overset y \underset. Úselo para colocar material encima o debajo de cualquier símbolo ordinario o de relación o símbolo de operador binario.

El comando \sideset agrega decoraciones a cualquier símbolo del Operador (suma, producto, etc.) además de los límites normales. Estos se colocan en las posiciones de subíndice y superíndice a la izquierda y derecha del Operador.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]