Afinando fórmulas matemáticas | manual de látex

Ya hemos analizado la mayoría de las facilidades necesarias para construir fórmulas matemáticas. Pero todavía hay algunos puntos finos que le permitirán producir fórmulas realmente hermosas, fórmulas que mejorarán la apariencia general y la legibilidad de los libros y artículos que escribirá.

8.1. Puntuación

La regla general es: cuando una fórmula va seguida de un punto, coma, punto y coma, dos puntos, signo de interrogación, signo de exclamación, etc., poner la puntuación después de $, cuando la fórmula esté en el texto; pero coloque la puntuación antes de $$ cuando se muestre la fórmula. Por ejemplo,

If $x<0$, we have shown that $$y=f(x).$$

Por lo tanto, nunca deberías escribir nada como

for $x = a, b$, or $c$.

debería ser

for $x = a$, $b$, $c$.

En el primer caso, TeX escribirá $x = a, b$ como una fórmula única, poniendo así un espacio delgado entre la coma y la b. Este espacio no será el mismo que el espacio entre la coma y la c, ya que los espacios entre palabras siempre son más grandes que los espacios finos. Este espaciamiento parece malo, pero en el segundo caso el espaciamiento se verá bien.

También es importante que TeX nunca rompa una línea de un párrafo en el espacio entre la coma y la b porque los saltos después de las comas en las fórmulas suelen ser incorrectos, como en la ecuación $x = f(x, a)$. De este modo, se inhibe la posibilidad de romper líneas en un párrafo, lo que conduce a una peor apariencia del documento tipográfico. En otras palabras, si un signo de puntuación pertenece lingüísticamente a la oración y no a la fórmula, déjelo fuera de los $.

8.2. Letras no cursivas

Las funciones matemáticas comunes como “log” siempre están configuradas en tipo romano. La mejor manera de incluir dichos objetos en una fórmula es utilizar los siguientes comandos:

En los siguientes ejemplos se utilizan algunos de estos comandos:

Las dos últimas fórmulas mostradas muestran que TeX trata algunos de los comandos como operadores grandes con límites como el signo de suma. Y el subíndice de \max no se trata como el subíndice de \log. Los subíndices y superíndices se convertirán en límites cuando se agreguen a \det, \gcd, \inf, \lim, \liminf, \limsup, \max, \min , \Pr y \sup, en estilo de visualización.

Si necesita un tipo romano para una función u operador de uso frecuente que no figura en la lista anterior, puede definir fácilmente su propio comando. Supongamos que desea definir un operador con límites y llamarlo \oper. Para ello deberá incluir en el preámbulo la siguiente definición:

\def\oper{\mathop{\rm oper}}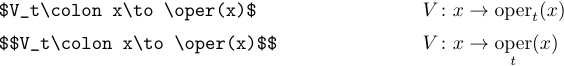

En caso de que se suponga que su operador no tiene límites, utilice una definición como la siguiente:

\def\oper{\mathop{\rm oper}\nolimits}

Si necesita el tipo romano para un solo uso, es más fácil cambiar al tipo \rm de la siguiente manera:

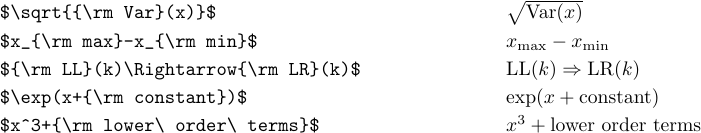
Observe los usos de ‘\ ’ en el último caso. Sin ellos, los espacios en blanco ordinarios se habrían ignorado y los “términos de orden inferior” se habrían escrito como “términos de orden inferior”.

La palabra “mod”, que también suele aparecer en tipografía romana en las fórmulas, necesita más cuidado, porque se utiliza de dos maneras diferentes. LaTeX proporciona el comando \bmod que se usará cuando “mod” sea una operación binaria y el comando \pmod que se usará cuando “mod” aparezca entre paréntesis al final de una fórmula.

Observe que \pmod inserta sus propios paréntesis; la cantidad que aparece después de “mod” entre paréntesis debe estar entre llaves a menos que sea un símbolo único.

También puede obtener otros estilos de tipo de la misma manera que obtiene el tipo romano usando \rm. Por ejemplo, \bf aparece en negrita:

Puedes notar que ‘+’ y ‘=" todavía están en tipo romano. LaTeX configura las cosas para que comandos como \rm y \bf afecten solo las letras mayúsculas A a Z, las letras minúsculas a a z, los dígitos 0 a 9 , las letras griegas mayúsculas \Gamma hasta \Omega y acentos matemáticos como \hat y \tilde. Por cierto, no se utilizaron llaves en este ejemplo, ya que los $ tienen el efecto de agrupar; \bf cambia la fuente actual, pero el cambio es local, por lo que no afecta la fuente actual fuera de la fórmula.

También puedes decir \cal en fórmulas para obtener letras mayúsculas en un estilo “caligráfico”.

Esto sólo funciona con las letras A a Z; obtendrá resultados extraños si aplica \cal a letras minúsculas o griegas.

También está \mit, que significa “cursiva matemática”. Esto afecta al griego en mayúsculas.

Cuando “\mit” está en vigor, las letras ordinarias “A” a “Z” y “a” a “z” no cambian; están en cursiva como de costumbre, porque normalmente provienen de la fuente matemática cursiva. Por el contrario, las letras griegas mayúsculas y los acentos matemáticos no se ven afectados por “\rm”, ya que normalmente provienen de la fuente romana.

Con LaTeX, también puedes escribir \it o \tt para obtener texto en cursiva o letras de máquina de escribir en tu fórmula. Probablemente se pregunte por qué se proporcionan tanto \mit como \it. La respuesta es que \mit es “cursiva matemática” (que suele ser mejor para fórmulas) y \it es “cursiva de texto” (que suele ser mejor para ejecutar texto).

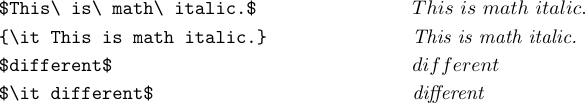
Las letras en cursiva matemática son más anchas y el espaciado es diferente. Esto funciona mejor en la mayoría de las fórmulas, pero la apariencia se ve afectada cuando intentas escribir ciertas palabras en cursiva como “diferente” en el modo matemático. Una ‘f’ en cursiva ancha suele ser deseable en las fórmulas, pero no en el texto. Por lo tanto, es mejor usar \it en una fórmula que se supone que contiene una palabra en cursiva. Por lo general, este no es un caso de matemáticas clásicas, pero es un caso común cuando se escriben programas de computadora:

El segundo ejemplo muestra el uso de subrayados cortos para dividir los nombres de los identificadores.

8.3. Espaciado entre fórmulas

Es un caso común cuando una pantalla contiene más de una fórmula; por ejemplo, una ecuación puede ir acompañada de una condición secundaria:

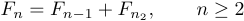
En tales casos necesitas decirle a TeX cuánto espacio poner después de la coma, porque las convenciones normales agruparían las cosas. Para obtener esto, puedes escribir

$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.

Aquí, \qquad significa “doble cuádruple”, donde “cuádruple” significa cierta cantidad de espacio que es común para las impresoras. Por lo tanto, \quad significa el cuádruple espacio de una impresora en la dirección horizontal. Siempre que desee un espaciado que difiera de las convenciones normales, debe especificarlo explícitamente mediante comandos como \quad y \qquad.

Un quad solía ser una pieza cuadrada en blanco, de 1 cm de ancho y 1 cm de alto, aproximadamente del tamaño de una M mayúscula; pero el quad de LaTeX no tiene altura.

En el texto de un párrafo, las fórmulas se ven mejor si están separadas por palabras, no solo por comas. Pero si realmente no hay texto para insertar, al menos deberías dejar algo de espacio entre las fórmulas. Comparar

The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.

y

The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.

que dan

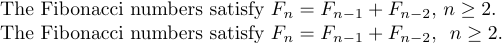
El ‘' aquí da una separación visual que compensa en parte el mal estilo.

8.4. Espaciado dentro de fórmulas

Ya hemos visto que TeX realiza un espaciado automático de las fórmulas matemáticas, lo que las hace lucir correctas en la mayoría de los casos. Sin embargo, es natural que surjan excepciones, ya que la cantidad de fórmulas posibles es enorme y las reglas de espaciado de TeX son bastante simples. Por lo tanto, es deseable tener unidades finas de espaciado para tales casos, en lugar de las piezas grandes que surgen de \ , \quad y \qquad.

Los elementos básicos del espacio que TeX pone en fórmulas se llaman espacios delgados, espacios medianos y espacios gruesos. TeX los inserta en fórmulas automáticamente, pero puedes agregar tu propio espaciado cuando quieras, usando los comandos

Las fórmulas que involucran cálculo se ven mejor cuando se inserta un espacio extra delgado antes de dx o dy o d lo que sea; pero TeX no hace esto automáticamente. Los siguientes ejemplos muestran cómo informar a TeX sobre estas necesidades:

Observe que no se necesitaba \, después de ‘/’ en la penúltima fórmula. Tampoco hay necesidad de \, en el último ejemplo, ya que dt aparece por sí solo en el numerador de una fracción; esto lo separa visualmente del resto de la fórmula.

Las unidades físicas, cuando aparecen en una fórmula, deben estar escritas en tipo romano y separadas del material anterior por un espacio delgado:

También se deben insertar espacios finos después de los signos de exclamación (operación factorial), si el siguiente carácter es una letra, un dígito o un delimitador de apertura:

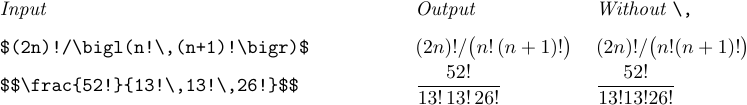
Además de estos casos, ocasionalmente encontrarás fórmulas en las que los símbolos están demasiado agrupados o en las que aparece demasiado espacio en blanco, debido a ciertas combinaciones desafortunadas de formas. Un \, o \! aplicado con buen gusto abrirá o cerrará las cosas para que el lector no se distraiga del significado matemático de la fórmula. Los radicales y las integrales múltiples suelen ser candidatos para este ajuste fino. A continuación se muestran algunos ejemplos de situaciones a tener en cuenta:

Las reglas de espaciado de TeX a veces fallan cuando ‘|’ y ‘\|’ aparecen en una fórmula, porque estos símbolos se tratan como símbolos ordinarios en lugar de delimitadores. Considere las fórmulas

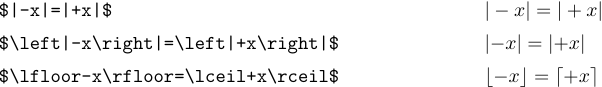
En el primer caso, el espaciado es incorrecto porque TeX cree que el signo más está calculando la suma de ‘|’ y ‘x’. El uso de \left y \right en el segundo ejemplo coloca a TeX en el camino correcto. El tercer ejemplo muestra que no se necesitan tales correcciones con otros delimitadores, porque TeX sabe si son aperturas o cierres.

8.5. elipses

Una elipsis puede indicarse mediante dos tipos diferentes de puntos, uno más alto que el otro. Las mejores tradiciones distinguen entre estas dos posibilidades. Generalmente es correcto producir fórmulas como

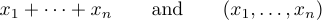
pero es incorrecto producir fórmulas como

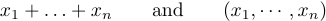
La idea es escribir \ldots cuando desee tres puntos bajos y \cdots cuando desee tres puntos centrados verticalmente. En general, es mejor usar \cdots entre + y - y signos de multiplicación, y también entre signos = o signos “menor o igual” o signos de subconjunto u otras relaciones similares. Los puntos bajos se utilizan entre comas y cuando las cosas se yuxtaponen sin ningún signo entre ellas:

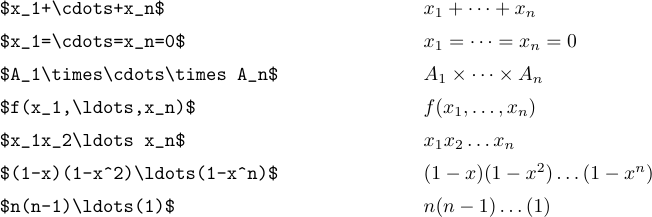Pero hay un caso especial en el que \ldots y \cdots no producen el espaciado correcto. Esto sucede cuando aparecen al final de una fórmula o justo antes de un delimitador de cierre. En tales situaciones se necesita un espacio extra fino. Por ejemplo, considere las siguientes oraciones:

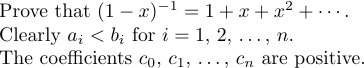
La primera frase se produce escribiendo

Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.

Sin \, el punto se habría acercado demasiado a \cdots.

La segunda oración fue escrita como:

Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.

Observe el uso de vínculos (~), que evitan saltos de línea incorrectos. Estas elipses son muy comunes en algunas formas de escritura matemática, por lo que LaTeX proporciona la macro \dots como abreviatura de $\ldots\,$ para usar en el texto de un párrafo. Por lo tanto, la tercera oración se puede escribir

The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.

8.6. Salto de línea

Cuando tienes fórmulas en un párrafo, es posible que TeX tenga que dividirlas entre líneas. Romperá una fórmula solo después de un símbolo de relación, o después de un símbolo de operación binaria, donde la relación u operación binaria está en el nivel externo de la fórmula, lo que significa que no está encerrada en {...}. Por ejemplo, si escribe

$f(x,y) = x^2-y^2 = (x+y)(x-y)$

en el medio del párrafo, existe la posibilidad de que TeX se rompa después de cualquiera de los signos = (preferido) o después de - o + o - (en caso de emergencia). Pero en ningún caso habrá una pausa después de la coma, ya que las comas después de las cuales son deseables las pausas no deberían aparecer entre $.

Si no desea permitir la interrupción en este ejemplo, excepto después de los signos =, puede escribir

$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$

porque estos apoyos adicionales “congelan” las subfórmulas, metiéndolas en cajas irrompibles. Pero no hay necesidad de preocuparse por tales cosas a menos que TeX realmente rompa una fórmula, ya que la posibilidad de que esto ocurra es bastante baja.

Si desea permitir la interrupción en algún punto del nivel externo de una fórmula, puede decir \allowbreak. Por ejemplo, si la fórmula

$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$

aparece en el texto de un párrafo, TeX permitirá dividirlo en dos partes

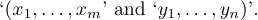
8.7. Tirantes

Los símbolos ‘{’ y ‘}’ se utilizan en varias notaciones diferentes, y LaTeX proporciona algunos comandos para ayudarle a manejar fórmulas que involucran tales cosas. El caso más simple es cuando se utilizan llaves para indicar un conjunto de elementos. Por ejemplo, “{a, b, c}” representa el conjunto de tres elementos a, b y c:

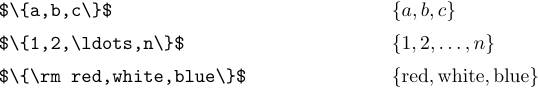
Un conjunto también puede indicarse dando un elemento genérico seguido de una condición específica. Por ejemplo, el conjunto de todos los objetos x que son mayores que 5 se puede escribir de la siguiente manera:

Se trata de dos variantes para indicar un mismo conjunto. El primero requiere usar \mid para obtener la barra vertical, mientras que el segundo no requiere nada excepto los dos puntos, que se trata como una operación binaria.

Cuando los delimitadores crecen, deben llamarse \bigl, \bigm y \bigr:

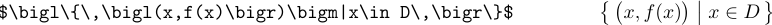
Las fórmulas con delimitadores aún mayores usarían comandos \Big o \bigg o incluso \Bigg.

También puede encontrar otro uso de llaves en las fórmulas mostradas. En realidad, es una llave izquierda que indica una elección entre varias alternativas:

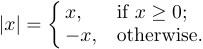
Esta construcción se puede escribir usando el comando \case:

$$|x|=\case{x,&if $x\ge0$;\cr
            -x,&otherwise.\cr}$$

Cada uno de los casos tiene dos partes separadas por el símbolo “&”, que juega un papel especial en la construcción de estructuras tabulares. A la izquierda de & hay una fórmula matemática que está implícitamente encerrada en $...$; a la derecha de & hay texto normal. Entonces, -x, en la segunda línea se escribirá en modo matemático, pero de lo contrario se escribirá en modo horizontal. Los espacios en blanco antes y después de “&” se ignoran. Puede haber cualquier número de casos, aunque normalmente son sólo dos. Cada caso debe ir seguido de \cr.

Las llaves horizontales se colocarán encima o debajo de partes de una fórmula mostrada si usa los comandos \overbrace o \underbrace. Estas cosas se consideran operadores grandes como \sum, por lo que puedes poner límites encima o debajo de ellos especificando superíndices o subíndices:

8.8. matrices

Las matrices son objetos bastante comunes en fórmulas matemáticas; son simplemente conjuntos rectangulares de fórmulas dispuestas en filas y columnas. LaTeX proporciona el comando \matrix para tratar con los tipos más comunes de matrices.

Por ejemplo, supongamos que desea especificar la visualización

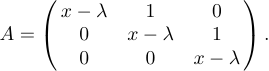
Todo lo que haces es escribir

$$A=\left(\matrix{x-\lambda&1&0\cr
                  0&x-\lambda&1\cr
                  0&0&x-\lambda\cr}\right).$$

Esto es bastante similar a la construcción \cases que vimos anteriormente; cada fila de la matriz va seguida de \cr y los signos & se utilizan entre las entradas individuales de cada fila. Sin embargo, a diferencia de \cases, se supone que debes colocar tus propios delimitadores \left y \right alrededor de la matriz. La razón es que se pueden utilizar diferentes delimitadores en diferentes construcciones de matrices. Por otro lado, los paréntesis se usan con más frecuencia que otros delimitadores, por lo que puedes escribir \pmatrix si quieres que LaTeX establezca los paréntesis por ti:

$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$

Cada entrada de una matriz normalmente está centrada en su columna, y cada columna se expande tanto como sea necesario para acomodar las entradas que contiene, y hay un espacio cuádruple entre columnas. Si desea que algo salga alineado hacia la izquierda/derecha en su columna, sígalo/precédalo por \hfill.

Cada entrada de una matriz se procesa por separado de las demás y se compone como una fórmula matemática en estilo de texto. Así, por ejemplo, si dice \rm en una entrada, no afecta a las demás. Decir {\rm x&y} no es válido.

Las matrices suelen aparecer como patrones genéricos que utilizan elipses para indicar filas o columnas que quedan fuera. Puede componer dichas matrices colocando las elipses en sus propias filas y/o columnas. Además de \ldots, LaTeX proporciona \vdots (puntos verticales) y \ddots (puntos diagonales) para este tipo de construcciones. Considere la siguiente matriz

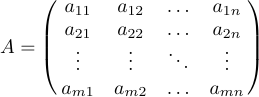
que se especifica como:

$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
             a_{21}&a_{22}&\ldots&a_{2n}\cr
             \vdots&\vdots&\ddots&\vdots\cr
             a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$

A veces, una matriz está bordeada en la parte superior e izquierda por fórmulas que dan etiquetas a las filas y columnas. Para esta situación, se define en LaTeX una macro especial llamada \bordermatrix. Por ejemplo, la pantalla

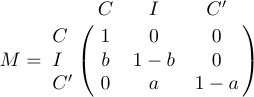
se obtiene al escribir

$$M=\bordermatrix{&C&I&C'\cr
                C&1&0&0\cr
                I&b&1-b&0\cr
                C'&0&a&1-a\cr}$$

La primera fila muestra las etiquetas superiores, que aparecen encima de los grandes paréntesis izquierdo y derecho; la primera columna proporciona las etiquetas de la izquierda, que están escritas a ras de la izquierda, justo antes de la propia matriz. El elemento en la intersección de la primera columna y la primera fila normalmente está en blanco. Y al igual que \pmatrix, \bordermatrix inserta sus propios paréntesis.

Por lo general, no es aconsejable poner matrices en el texto de un párrafo. La razón es que son tan grandes que se muestran mejor. Pero aún así, es posible que en ocasiones quieras descuidar esto. En este caso, puede utilizar \choose o \atop:

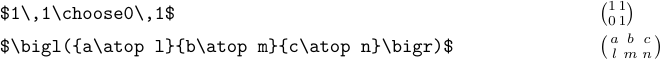
La macro \matrix no produce matrices pequeñas como esta.