7. Ajustes de tamaño previo al diseño | manual de látex

Por lo general, LaTeX hace un gran trabajo al diseñar fórmulas matemáticas. Pero a veces es necesario un ajuste más preciso del posicionamiento. Este artículo analiza algunas técnicas para ajustar el diseño y mejorar un poco las fórmulas matemáticas.

7.1. Dimensionamiento y espaciado automáticos

Los símbolos y letras matemáticos generalmente se vuelven más pequeños (y con espacios más ajustados) cuando aparecen en fracciones, subíndices o superíndices. Las fórmulas matemáticas se pueden presentar en ocho estilos matemáticos TeX:

D, D'	\displaystyle	Se muestran en líneas independientes
T, T'	\textstyle	Se incrustan en el texto
S, S'	\scriptstyle	En superíndices o subíndices
SS, SS'	\scriptscriptstyle	En todos los superíndices o subíndices de orden superior

El estilo de texto (T) se usa en el nivel superior de una fórmula que se establece en el texto en ejecución (entre un par de $ o entre \( y \)), mientras que el estilo de visualización se usa en el nivel superior. nivel superior de una fórmula mostrada (entre un par de $$ o entre \[ y \]). En cuanto a las subfórmulas, el estilo se puede determinar a partir de la siguiente tabla:

D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

El siguiente ejemplo ilustra los distintos estilos:

\normalsize                 %% Style:
\[ b                        %% D
    ^0                      %% S
   +                        %% D
   \frac{(k + p)            %% T
          _{j'}             %% S'
         % \displaystyle
         \pm                %% T [D]
         \frac{(f + q)      %% S [T]
                ^{(pk)      %% SS [S]
                   ^y       %% SS
                   _{j'}}}  %% SS'
              {(h + y)}}    %% S' [T']
        {(l + q)            %% T'
          ^{(pk)}}          %% S'
\]

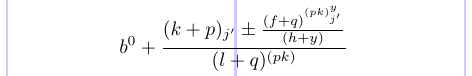
Puedes eliminar el carácter de comentario (%) antes de \displaystyle y ver cómo algunos de los estilos han cambiado a los que están entre paréntesis:

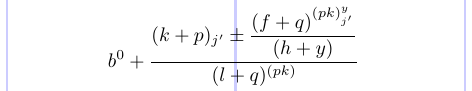
Muestra cómo especificar explícitamente el estilo que se utilizará en cada parte.

7.2. Subfórmulas

En el texto, un par de llaves indica un grupo o un ámbito dentro del cual alguna declaración está en vigor. Dentro de una fórmula matemática, además, delimitan una subfórmula, que siempre se compone como una entidad separada que se agrega a la fórmula externa. Como consecuencia, las subfórmulas siempre se escriben en su ancho natural y no se estiran ni encogen horizontalmente cuando TeX construye un párrafo tratando de encajar la fórmula en una línea. Ya hemos demostrado que la subfórmula de un grupo de llaves simple se procesa como si fuera un símbolo único. Esto significa que un grupo vacío produce un símbolo invisible que puede cambiar el espaciado.

El contenido de los subíndices/superíndices y los argumentos de muchos (pero no todos) comandos, como \frac y \mathrel, también son subfórmulas. Por tanto, reciben el mismo trato especial. El argumento de \bm, por ejemplo, no necesariamente se establece como una subfórmula, y esta es una de las excepciones importantes. En una fórmula matemática, si solo necesita limitar el alcance de una declaración, defina un grupo usando \begingroup y \endgroup. Recuerde que las declaraciones matemáticas especializadas, como los cambios de estilo, se aplican hasta el final de la subfórmula actual, independientemente de si hay otros grupos presentes o no.

7.3. Grandes delimitadores

LaTeX define cuatro comandos: \big, \Big, \bigg y Bigg, para proporcionar control directo de los tamaños de los delimitadores extensibles. Toman un único argumento, que debe ser un delimitador extensible, y producen versiones más grandes del delimitador, de 1,2 a 3 veces el tamaño base.

También hay tres variantes para cada uno de los cuatro comandos, dando cuatro tamaños de Símbolo de apertura (\bigl, \Bigl, \biggl y \Biggl); cuatro tamaños de Símbolo de relación (\bigm, \Bigm, \biggm y \Biggm); y cuatro tamaños de símbolo de cierre (\bigr, \Bigr, \biggr y \Biggr). Estos 16 comandos deben usarse con cualquier símbolo que pueda venir después de \left, \right o (con eTeX) \middle (consulte esta tabla).

Los tamaños de estos delimitadores están fijados en LaTeX estándar. Sin embargo, con el paquete amsmath, los tamaños se adaptan al tamaño del material circundante, según el tamaño de fuente y el estilo matemático utilizado. Esto se muestra en el siguiente ejemplo.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
\Large
\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]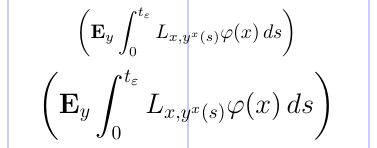

7.4. Ajustando el índice de forma radical.

La ubicación del índice en un signo radical no siempre es buena en LaTeX estándar. Sin embargo, puede utilizar los comandos \leftroot y \uproot definidos en el paquete amsmath para ajustar la posición de este índice. Los argumentos enteros positivos para estos comandos mueven el índice hacia la izquierda y hacia arriba, respectivamente, mientras que los argumentos negativos lo mueven hacia la derecha y hacia abajo. Estos argumentos se dan en unidades matemáticas, que son bastante pequeñas, por lo que estos comandos son adecuados para realizar ajustes.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\[
  \sqrt[\beta]{k} \qquad
  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
\]

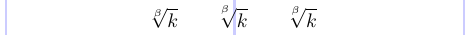
7.5. Puesta a punto con puntales y fantasmas

Siempre que desee componer “perfectamente” el espaciado y la alineación matemática, generalmente es mejor recurrir a las capacidades únicas y avanzadas del TeX primitivo. El acceso a estas funciones se proporciona mediante una serie de comandos relacionados con \phantom y \smash. Esos comandos se pueden usar en fórmulas matemáticas o en texto corriente.

Echemos un vistazo al siguiente ejemplo:

\usepackage{amsmath}
\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
\newcommand\bfE{\mathbf{E}}
% -------------------------------------------------------------------------------
\begin{equation} \begin{split}
  f_{h, \ve}(x, y)
    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
    &\relphantom{=} {} + h \biggl[
       \frac{1}{\tve}
       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
    &\relphantom{=} \phantom{{} + h \biggl[ }
       \frac{1}{\tve}
       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
                                            \vf(x) \,ds    \biggr) \biggr]
\end{split} \end{equation}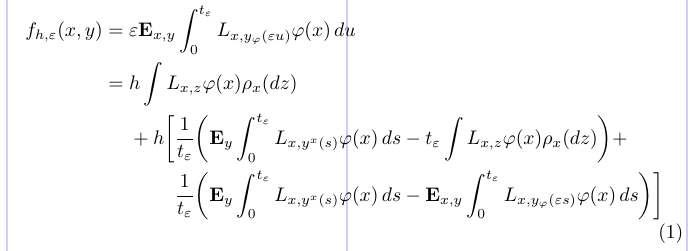

Aquí, el comando \phantom ajusta el posicionamiento horizontal. En el preámbulo, se utiliza para definir un símbolo de relación invisible de igual ancho que su argumento (= en este ejemplo). Dentro de los entornos matemáticos, se utiliza para alinear ciertas líneas comenzando con una subfórmula “fantasma” o invisible. El par de llaves vacías {} es lo mismo que \mathord{}, lo que produce un símbolo invisible de ancho cero necesario para obtener el espaciado correcto de “+ h” (sin {}, el signo más El signo producirá un signo más unario con un espaciado inadecuado antes de h).

A diferencia de \phantom, el comando \smash escribe su contenido (en un cuadro LR) pero luego ignora tanto su alto como su ancho, como si ambos fueran cero. El comando \hphantom, definido en LaTeX estándar, es una combinación de los dos. Produce el equivalente a \smash{\phantom{algunos contenidos fantasmas}}, es decir, un cuadro invisible con altura y profundidad cero pero con el ancho del contenido fantasma.

El comando \vphantom es similar, pero hace que el ancho del fantasma sea cero preservando su altura total más su profundidad. El comando \mathstrut se define como \vphantom( y produce un cuadro de ancho cero con altura y profundidad igual a la de un paréntesis.

Con el paquete amsmath, el comando \smash puede tomar un argumento opcional, de modo que \smash[t]{...} ignora la altura del contenido del cuadro, manteniendo la profundidad, mientras que \smash[ b]{...} ignora la profundidad y conserva la altura.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

Parece que darle a la y algo de altura adicional con un puntal hará que los radicales se vean similares. Pero, en cambio, sólo los hace parecer más diferentes y más feos en su conjunto. Resulta que romper el fondo de la y es la mejor manera.

El siguiente ejemplo muestra un uso muy común de aplastar. El comando \smash se utiliza allí para proporcionar un control preciso sobre la altura de los delimitadores circundantes. También muestra que el aplastamiento puede causar problemas ya que es necesario conocer la altura real de la línea. Esto lo repara \vphantom. \Hmjd es el símbolo compuesto definido como:

\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Para mostrar el espacio vertical resultante agregamos reglas:

Apariencia	Código	Comentario
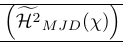	\left( {\Hmjd } \right)	Los corchetes externos son demasiado grandes
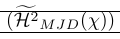	\left( \smash{\Hmjd } \right)	Los corchetes externos son demasiado pequeños y las reglas demasiado cercanas
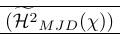	\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}	¡Perfecto!
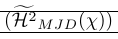	\left( \smash[t]{\Hmjd } \right)	Se necesitan tanto \vphantom como Smash parcial

En algunos lugares, las deficiencias en el procesamiento de TeX de bajo nivel pueden provocar errores en los detalles finos de la composición tipográfica. Esto puede suceder en diseños particulares donde (a) una subfórmula (numerador/denominador de una fracción o subíndice/superíndice) consiste exactamente en un cuadro LR, o un cuadro matemático construido de manera similar, y también (b) ese cuadro no tiene su tamaño natural, como sucede con las formas más complejas de \makebox, los smashes y algunos fantasmas.

Para ver esto, veamos el siguiente ejemplo:

\[
\sqrt{ \frac{a+b}{x_j} } \quad
\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
\sqrt{ \frac{a+b}{\smash{x_j+b}} }
\]

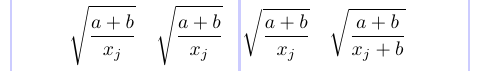
Para reducir la profundidad del radical, se añadió un \smash en el segundo radical, pero esto no tuvo ningún efecto. En el tercer radical trabajó con un grupo de tirantes vacío. Pero en el cuarto radical no se necesitó ningún grupo de refuerzo vacío. Para resumir, siempre que encuentre que \smash no funciona, intente agregar una subfórmula matemática vacía ({}) antes del cuadro solitario, para que se trate correctamente.

7.6. Espaciado horizontal

Un ajuste más preciso y más difícil requiere los comandos de espaciado explícitos que se muestran en la siguiente tabla:

Tanto la forma completa como la breve de estos comandos son sólidas y también se pueden usar fuera de las fórmulas matemáticas en el texto normal. Están relacionados con los espacios finos, medianos y gruesos disponibles en las máquinas utilizadas para componer matemáticas a mediados del siglo XX.

Los valores actuales de los tres parámetros TeX \thinmuskip, \medmuskip y \thickmuskip definen la cantidad de espacio agregado por estos comandos \..space. Sus valores predeterminados con “amsmath” se enumeran en la tabla. Estos parámetros de bajo nivel requieren valores en unidades matemáticas (mu). Por lo tanto, sólo se pueden configurar mediante asignaciones TeX de bajo nivel, no mediante \setlength o similar. Además, normalmente sus valores no deberían modificarse ya que son utilizados internamente por la composición tipográfica matemática de TeX (consulte la siguiente tabla).

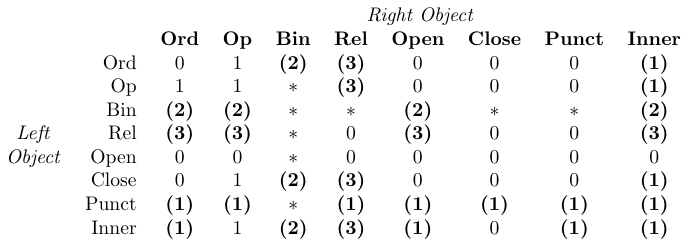
En la tabla, 0 significa “sin espacio”, 1 significa \thinmuspace, 2 significa \medmuskip, 3 significa \thickmuskip, * significa “imposible”. Las entradas en negrita significan que no se agrega el espaciado correspondiente en los estilos de escritura matemática.

Una unidad matemática (1mu) es igual a 1/18 de em en el tamaño de fuente matemática actual. De ello se deduce que el valor absoluto de mu varía con el estilo matemático, dando un espaciado consistente independientemente del estilo utilizado.