8. Fuentes en fórmulas matemáticas | Matemáticas de fuentes

Introducción a las fuentes LaTeX

A diferencia del texto flotante, generalmente no necesitará cambios automáticos en las formas de la fuente. Las diferentes formas tienen significados específicos en matemáticas. Por ejemplo, se pueden utilizar letras verticales en negrita para los vectores. Si los caracteres de una fórmula cambiaran debido a las condiciones del entorno, el resultado sería incorrecto. Por eso el manejo de las fuentes en las fórmulas matemáticas difiere del manejo de las fuentes en el texto.

Los caracteres de una fórmula se pueden dividir en dos clases: símbolos y caracteres alfabéticos (incluidos los dígitos). En realidad, TeX trata internamente con ocho clases que definen el espaciado apropiado. Pero para el debate actual, la división en dos clases es suficiente.

Algunos símbolos, como =, se pueden ingresar directamente desde el teclado. Sin embargo, parte de ellos se debe ingresar mediante un comando, por ejemplo, \leq da un signo menor o igual. El otro grupo principal de caracteres de una fórmula, los caracteres del alfabeto, se ingresan directamente desde el teclado.

Hay más de 200 símbolos predefinidos en LaTeX estándar. Permite al usuario escribir casi cualquier fórmula deseada. Estos símbolos están ubicados en varias fuentes diferentes, pero se puede acceder a ellos de tal manera que el usuario no tiene que ser consciente de cómo se representan internamente. Si es necesario, se pueden hacer accesibles fuentes de símbolos adicionales de forma similar.

Los símbolos y los caracteres del alfabeto tienen una diferencia que es más importante para nosotros ahora: los símbolos tienen la misma representación gráfica dentro de una fórmula, mientras que el usuario puede cambiar la apariencia de los caracteres del alfabeto. Los comandos que cambian la apariencia de los caracteres alfabéticos en una fórmula se denominan identificadores del alfabeto matemático, y las fuentes asociadas con estos comandos se denominan alfabetos matemáticos. Una fórmula no cambia si se coloca, por ejemplo, dentro de un entorno de teorema donde el texto está escrito en cursiva de forma predeterminada, porque los identificadores alfabéticos son independientes de los comandos de fuente circundantes fuera de la fórmula. Este comportamiento es muy importante porque las formas de los caracteres conllevan significados que deben permanecer sin cambios dondequiera que aparezca la fórmula en un documento.

8.1. Identificadores del alfabeto matemático

Un alfabeto y una gran cantidad de símbolos no son suficientes para los científicos. Intentan utilizar todos los tipos de letra disponibles para indicar conceptos especiales. Además de los alfabetos extranjeros como las letras griegas, a las que normalmente se accede como símbolos - \alpha, \beta, etc. - podemos encontrar letras sans serif para matrices, letras serif en negrita para vectores, fuentes Fraktur para grupos, ideales o campos. Otros usan formas caligráficas para indicar conjuntos. El número de convenciones es infinito y difieren de una disciplina a otra. Y LaTeX se adapta a esto, haciendo posible declarar nuevos identificadores de alfabeto matemático y asociarlos con cualquier grupo de formas de fuente deseado en lugar de depender únicamente de un conjunto predefinido que no se puede ampliar. Estos identificadores son comandos especiales que se usan en una fórmula que escribe cualquier carácter del alfabeto en su argumento en un tipo de letra específico. Estos identificadores pueden usar diferentes tipos de letra en diferentes fórmulas, como veremos más adelante, pero dentro de una fórmula siempre seleccionan el mismo tipo de letra independientemente de las condiciones del entorno.

Identificadores de alfabeto predefinidos

LaTeX ya tiene algunos identificadores alfabéticos integrados. Se muestran en la siguiente tabla. Las dos últimas líneas muestran que las letras utilizadas en las fórmulas se toman del alfabeto matemático \mathnormal. Por otro lado, las letras producidas por \mathit tienen espacios diferentes, lo que significa que este alfabeto se puede utilizar para proporcionar nombres de variables de palabras completas que son comunes en algunas disciplinas.

Comando	Código de ejemplo	Resultado
`\mathcal`	$\mathcal{A}=a$	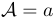$“A caligráfica es igual a a”$
`\mathrm`	$\mathrm{max}_i$	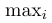$“Subíndice máximo romano i”$
`\mathbf`	$\sum x = \mathbf{v}$	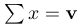$“Suma x en negrita es igual a v”$
`\mathsf`	$\mathsf{G}_1^2$	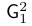$“G sin serifa, subíndice 1, superíndice 2”$
`\mathtt`	$\mathtt{W}(a)$	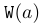$“Máquina de escribir W de a”$
`\mathnormal`	$\mathnormal{abc}=abc$	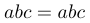$“Abc normal es igual a abc”$
`\mathit`	$differ\neq\mathit{differ}$	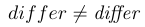$“Diferencia cursiva no es igual a diferencia”$

En LaTeX2e, los identificadores del alfabeto matemático son comandos con un argumento, una sola letra o una sola palabra que se escriben en una fuente especial.

1Therefore, $\mathsf{G}$ can be computed as
2\begin{equation}
3\mathsf{G} = \mathcal{A} +
4             \sum_{i=1}^{n} \mathcal{B}_{i}
5\end{equation}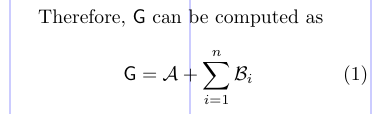

$Identificadores del alfabeto matemático predefinidos$

Alfabeto matemático predeterminado

Si no especifica explícitamente un identificador de alfabeto, ¿de qué alfabeto se seleccionan los caracteres del alfabeto? En otras palabras, ¿cuál es el alfabeto matemático predeterminado? La respuesta es que no existe un único alfabeto matemático predeterminado. El sistema LaTeX se puede configurar para que los caracteres alfabéticos se obtengan de diferentes alfabetos, a menos que el usuario solicite explícitamente uno específico, y este es normalmente el caso, como muestra el siguiente ejemplo.

1\begin{eqnarray}
2x &=& 12345 \\
3\mathrm{x} &=& \mathrm{12345} \\
4\mathnormal{x} &=& \mathnormal{12345}
5\end{eqnarray}

$Sin alfabeto matemático predeterminado$

Aquí puede ver que \mathrm no cambia los dígitos y \mathnormal no cambia las letras, por lo que el valor predeterminado para los dígitos en la configuración normal es el alfabeto matemático asociado con \mathrm y el El valor predeterminado para las letras es el asociado con \mathnormal. Este comportamiento se puede controlar con el comando \DeclareMathSymbol.

¿Qué fuente usa LaTeX para matemáticas?

En LaTeX, la fuente predeterminada utilizada para el modo matemático suele ser Computer Modern. Sin embargo, también puede utilizar diferentes fuentes especificándolas en el preámbulo de su documento LaTeX mediante paquetes.

Identificadores de alfabeto personalizados

Puede utilizar el comando \DeclareMathAlphabet para definir un nuevo identificador de alfabeto matemático. Supongamos que desea que un tipo de letra sans serif inclinado esté disponible como alfabeto matemático. Primero decide un nuevo nombre de comando, como \msfsl, que se utilizará como identificador alfabético. Luego, consulte la tabla de clasificación de fuentes a continuación para encontrar un grupo de formas de fuente adecuado para asignar a este identificador alfabético.

$Clasificación de las familias tipográficas Computer Modern$

Descubrirás que la familia Computer Modern Sans, por ejemplo, consta de una serie mediana con formas verticales e inclinadas. Si decide utilizar la forma inclinada de esta familia, dígaselo a LaTeX usando \DeclareMathAlphabet.

1\DeclareMathAlphabet{cmd}{encoding}{family}{series}{shape}

Hay cuatro parámetros (además del propio identificador) en la declaración: el nombre de codificación, la familia, la serie y la forma de la fuente que se utilizará. El identificador alfabético definido en el siguiente ejemplo siempre cambiará a Computer Modern Sans medio inclinado.

1\DeclareMathAlphabet{\msfsl}{OT1}{cmss}{m}{sl}
2% -------------------------------------------------------------------------------
3We demonstrate this with the formula
4\begin{equation}
5\sum \msfsl{A}_{i} = a \tan \beta
6\end{equation}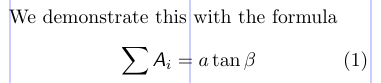

$Declaración de un identificador de alfabeto matemático personalizado$

También puede redefinir un identificador de alfabeto matemático existente en un archivo de paquete o en el preámbulo de su documento. Por ejemplo,

1\DeclareMathAlphabet{\mathsf}{OT1}{pag}{m}{n}

anulará la configuración predeterminada para el identificador alfabético \mathsf. Cambiará a Adobe Avant Garde en sus fórmulas.

Tenga en cuenta que si el alfabeto matemático en cuestión es parte de una fuente de símbolos que ya está cargada por LaTeX por otras razones (por ejemplo, \mathcal), es mejor usar \DeclareSymbolFontAlphabet ya que hace un mejor uso de los recursos algo limitados de TeX para las matemáticas.

Las mejores fuentes matemáticas

Además de la fuente predeterminada Computer Modern, LaTeX ofrece siete fuentes integradas para componer alfabetos matemáticos, de modo que los usuarios puedan personalizar sus expresiones matemáticas sin necesidad de paquetes adicionales en el preámbulo. Y la mejor opción para ti es utilizar una de estas 8 fuentes.

Fuente	Uso	Comando
Roman vertical	Fuente vertical estándar	`\mathrm{}`
Caligráfica	Se utiliza para componer letras matemáticas regulares.	`\mathnormal{}`
Caligráfica	Se utiliza para componer letras mayúsculas con una fuente caligráfica especial.	`\mathcal{}`
Letras cursivas	Convertir el texto en cursiva	`\mathit{}`
Sans Serif vertical	Establece letras Sans Serif verticales	`\mathsf{}`
Roman vertical en negrita	Se utiliza para componer letras Roman vertical en negrita	`\mathbf{}`
Tipo de máquina de escribir	Se utiliza para componer letras tipográficas de máquina de escribir en posición vertical.	`\mathtt{}`

8.2. Comandos de fuentes de texto en matemáticas

Aunque las declaraciones de fuentes de texto como \rmfamily no se pueden usar en matemáticas, los comandos de cambio de fuente, por ejemplo, \textrm, se pueden usar tanto en texto como en matemáticas. Con estos comandos, puede cambiar temporalmente del contexto matemático al de texto y componer algo de texto en medio de su fórmula que lógicamente es parte del texto circundante fuera de la fórmula. La fuente utilizada para componer este texto dependerá de las condiciones del entorno, lo que significa que heredará la codificación, familia, serie y forma actuales, como en el siguiente ejemplo.

1\sffamily The result will be
2\[ x = 10 \textbf{ and thus } y = 12 \]

$Comandos de fuente de texto en matemáticas$

Aquí podemos ver que se mantuvo la familia Sans y la serie se cambió a negrita. El comando \text proporcionado por el paquete amstext (que también carga amsmath) puede resultar más útil. Recoge los valores actuales de codificación, familia, serie y forma sin cambiar ninguno de ellos.

8.3. Versiones de fórmulas matemáticas

Hemos discutido cómo cambiar partes de una fórmula usando identificadores del alfabeto matemático. LaTeX también te permite cambiar la apariencia de una fórmula en su conjunto. Las fórmulas matemáticas siempre se escriben en una determinada versión matemática. Y puedes cambiar entre versiones matemáticas fuera del modo matemático usando el comando \mathversion, que cambia el diseño general de las siguientes fórmulas.

LaTeX tiene dos versiones matemáticas por defecto: normal y negrita. Y los paquetes especiales proporcionan más versiones. Por ejemplo, el paquete mathtime (para las fuentes comerciales MathTime) configura una versión matemática llamada heavy para componer fórmulas con símbolos ultra negritas como los que proporcionan las fuentes MathTime.

Obviamente, la versión matemática predeterminada es \mathversion{normal}. La versión en negrita, a su vez, producirá caracteres alfabéticos y símbolos más en negrita, aunque los operadores grandes, como \sum, no se modifican de forma predeterminada. El siguiente ejemplo muestra la misma fórmula primero en la versión matemática normal y luego en negrita.

1\begin{equation}
2  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
3\end{equation}
4\mathversion{bold}
5\begin{equation}
6  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
7\end{equation}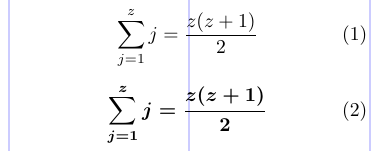

$Versiones matemáticas$

Usar \mathversion puede ser adecuado en determinadas situaciones, como en los títulos, pero hay que tener en cuenta que cambiar la versión significa cambiar la apariencia y posiblemente el significado de toda la fórmula. Si desea oscurecer sólo algunos símbolos o caracteres dentro de una fórmula, debe usar el identificador alfabético \mathbf para los caracteres y/o usar el comando \bm proporcionado por el paquete bm en lugar de cambie la \mathversion.

Cuando cambia la versión matemática, LaTeX busca en sus tablas internas dónde se encuentran todos los símbolos para esta nueva versión matemática. También puede cambiar todos o algunos de los identificadores del alfabeto matemático y asociarlos con otras formas de fuente en esta versión.

Pero, ¿qué sucede con los identificadores alfabéticos personalizados como \msfsl que definimos en el ejemplo? Siempre que los declares usando \DeclareMathAlphabet, seguirán siendo los mismos en todas las versiones matemáticas.

Si el identificador del alfabeto matemático va a producir una fuente diferente en una versión matemática especial, debe informarle a LaTeX usando el comando \SetMathAlphabet. Por ejemplo, en la configuración predeterminada, el identificador alfabético \mathsf se define de la siguiente manera:

1\DeclareMathAlphabet{\mathsf}{OT1}{cmss}{m}{n}
2\SetMathAlphabet{\mathsf}{bold}{OT1}{cmss}{bx}{n}

La primera línea establece el medio Computer Modern Sans como predeterminado para \mathsf en todas las versiones matemáticas. La segunda línea indica a LaTeX que use Computer Modern Sans negrita extendida en la versión matemática en negrita.

1\SetMathAlphabet{cmd}{version}{encoding}{family}{series}{shape}

Como habrás adivinado en el ejemplo anterior, \SetMathAlphabet toma seis argumentos: el identificador del alfabeto matemático, el nombre de la versión matemática para la cual estás definiendo una configuración especial y cuatro parámetros para identificar la fuente con la que estás asociando. su configuración. Como señalamos anteriormente, puede redefinir un identificador de alfabeto matemático existente usando \DeclareMathAlphabet. Si lo hace, todas las declaraciones \SetMathAlphabet anteriores para este identificador se eliminan de la memoria interna de LaTeX. Por lo tanto, el identificador aparecerá igual en todas las versiones matemáticas a menos que le agregue nuevas declaraciones \SetMathAlphabet.

8.4. Ajuste de fuentes en fórmulas con paquetes AMS-LATEX

El paquete amsfonts (y amssymb) define dos alfabetos matemáticos: el alfabeto Euler Fraktur (\mathfrak) y el alfabeto Blackboard Bold (\mathbb). Vea el ejemplo a continuación.

1\usepackage{amsfonts}
2% -------------------------------------------------------------------------------
3$ \forall n \in \mathbb{N} : \mathfrak{M}_n \leq \mathfrak{A} $

$identificadores del alfabeto matemático de amsfonts$

5. Estilo de fuente matemática en negrita. El paquete `bm`

Solo para letras latinas, puede usar el comando \mathbf. Para todo lo demás, existe el paquete bm. Simplemente cárguelo y use \bm para hacer que cualquier fórmula sea tan llamativa y hermosa como lo permitan las fuentes disponibles.

El siguiente ejemplo muestra muchas formas de utilizar los comandos \bm y \mathbf. También muestra una estrategia para definir nombres abreviados para símbolos en negrita que aparecen con frecuencia, utilizando \newcommand y \bmdefine estándar de LaTeX, que proporciona el paquete bm. Tenga en cuenta que \mathbf{xy} no es idéntico a \bm{xy}. El primero produce “xy” romano en negrita y el segundo produce “xy” (negrita cursiva matemática).

 1\usepackage{amsmath,amssymb,bm}
 2\newcommand\bfB{\mathbf{B}} \newcommand\bfx{\mathbf{x}}
 3\bmdefine\bpi{\pi} \bmdefine\binfty{\infty}
 4% -------------------------------------------------------------------------------
 5\section{The bold equivalence
 6  $\sum_{j < B} \prod_\lambda : \bm{\sum_{x_j} \prod_\lambda}$}
 7\begin{gather}
 8  B_\infty + \pi B_1 \sim \bfB_{\binfty} \bm{+} \bpi \bfB_{\bm{1}}
 9    \bm {\sim B_\infty + \pi B_1}\\
10  B_\binfty + \bpi B_{\bm{1}} \bm{\in} \bm{\biggl\lbrace}
11    (\bfB, \bfx) : \frac {\partial \bfB}{\partial\bfx}
12    \bm{\lnapprox} \bm{1} \bm{\biggr\rbrace}
13\end{gather}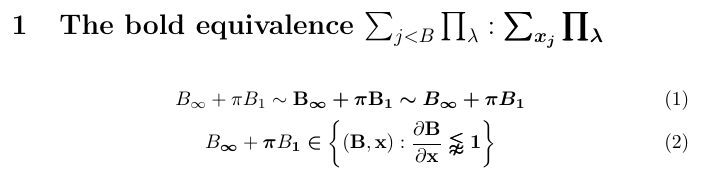

$Usando el paquete bm$

En este ejemplo, bm hace todo lo posible para cumplir con las solicitudes de versiones en negrita de símbolos y letras individuales. Pero si miras de cerca, verás que los resultados no siempre son óptimos. Por ejemplo, los operadores de suma y producto se crean con una técnica conocida como negrita del pobre, en la que el símbolo se sobreimprime tres veces con ligeros desplazamientos. Además, las llaves no están en negrita en absoluto. Estos inconvenientes no se pueden evitar porque para algunos símbolos simplemente no hay una variante en negrita cuando se utilizan las fuentes matemáticas Computer Modern.

¿Cuáles son las reglas exactas que sigue \bm para producir formas en negrita de los símbolos en su argumento? En general, utiliza el hecho de que LaTeX incluye una versión matemática negrita (accesible a través de \boldmath) para escribir una fórmula completa en negrita (siempre que haya fuentes de negrita adecuadas disponibles y configuradas). Para cada símbolo, el comando \bm mira esta versión matemática para ver qué se haría en esa versión. Si la fuente seleccionada para el símbolo es diferente de la seleccionada en la versión matemática normal, entonces escribe el símbolo en esta fuente en negrita, obteniendo un resultado perfecto (suponiendo que la versión matemática en negrita se configuró correctamente). Si las fuentes en ambas versiones son idénticas, se supone que no hay ninguna variante en negrita disponible y se aplica la negrita del pobre.

¡Cargue el paquete bm después de los paquetes que cambian la configuración de fuente matemática existente!

La situación es aún más compleja con delimitadores, como \biggl\lbrace en el ejemplo. TeX normalmente escribe un delimitador mediante un glifo elegido para que coincida con una altura solicitada de una secuencia de diferentes tamaños. Estos glifos se pueden ubicar en diferentes fuentes y un tamaño particular puede tener o no variantes en negrita. Todo esto en conjunto hace imposible que \bm determine de manera confiable si necesita aplicar la negrita del pobre. Por lo tanto, escribe el delimitador utilizando cualquier fuente que ofrezca la versión matemática en negrita. Con las fuentes matemáticas Computer Modern, solo el tamaño de delimitador más pequeño está disponible en negrita; todos los demás tamaños provienen de fuentes que no tienen variantes en negrita.

1\usepackage{bm}
2% -------------------------------------------------------------------------------
3$\bm{\Biggl\lbrace\biggl\lbrace\Bigl\lbrace\bigl \lbrace \lbrace
4  \mathcal{Q}
5  \rangle \bigr\rangle\Bigr\rangle\biggr\rangle
6\Biggr\rangle}$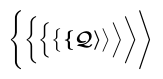

$Delimitadores puestos (y no puestos) en negrita por el comando \bm$ Normalmente, si un comando que a su vez toma argumentos está dentro del argumento de \bm, entonces ese comando debe estar completamente incluido en el argumento de \bm. Como resultado, todas las partes del material tipográfico aparecerán en negrita. Si necesita que la salida de un comando con argumentos esté solo parcialmente en negrita, debe hacer lo siguiente. Debe colocar los símbolos que no desea que estén en negrita en un \mbox y restablecer explícitamente la versión matemática dentro del contenido del cuadro usando \unboldmath. TeX considera que \mbox es un símbolo de clase Ordinario. Por lo tanto, para lograr el espaciado correcto, es posible que deba rodearlo con \mathbin, \mathrel o \mathop.

1\usepackage{amsmath,bm}
2% -------------------------------------------------------------------------------
3$ \bm{\sqrt[2]{x \times \alpha}} $ but
4$ \bm{\sqrt[2]{x \mathbin{\mbox{\unboldmath$\times$}} \alpha}} $
5or the similar
6$ \bm{\sqrtsign}{\bm{x} \times \bm{\alpha}} $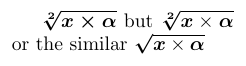

$\bm con comandos que toman argumentos$

Afortunadamente, rara vez se requieren operaciones tan complejas. En la mayoría de los casos que involucran comandos con argumentos, solo es necesario poner en negrita partes del argumento. Y esto se puede lograr usando el comando \bm dentro de esos argumentos. Al igual que con \sqrtsign en el ejemplo anterior, para el caso común de acentos en negrita, \bm está especialmente programado para permitir que el argumento del acento esté fuera de su propio argumento. Sin embargo, si necesita estos acentos con regularidad, es mejor definir sus propias abreviaturas, como en el ejemplo siguiente.

Mejorando el rendimiento

Aunque \bmdefine\bpi{\pi} parece ser simplemente una abreviatura de \newcommand\bpi{\bm{\pi}}, en realidad la verdad es casi lo contrario: \bm define un nuevo temporal oculto comando usando \bmdefine y luego usa inmediatamente este comando temporal para producir el símbolo en negrita. En otras palabras, \bmdefine hace todo el trabajo duro. Si usa con frecuencia, por ejemplo, algo que está definido mediante \bm{\alpha}, entonces se ejecuta un nuevo \bmdefine cada vez. Si proporciona la definición \bmdefine\balpha{\alpha} en el preámbulo, entonces \bmdefine realiza su laborioso trabajo solo una vez, sin importar cuántas veces se use \balpha.

1\usepackage{bm}
2\bmdefine\bhat{\hat}
3% -------------------------------------------------------------------------------
4$\hat a \neq \bm{\hat a} \neq \bm\hat a = \bhat a\neq \bm\widehat a$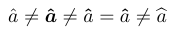

$Optimizado para poner acentos en negrita con el comando \bm$

Este ejemplo también muestra que los acentos de ancho variable (por ejemplo, \widehat) comparten una deficiencia con los delimitadores: en la configuración matemática Computer Modern provienen de una fuente para la cual no hay ninguna variante en negrita disponible.

Ajustes de tamaño previo al diseño. Símbolos en LaTeX.