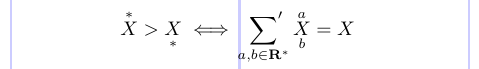4. Symboles décorés et structures composées | Manuel LaTeX

Le package amsmath fournit quelques commandes pour produire des structures telles que des objets ressemblant à des fractions et des symboles décorés. Cette discussion couvre certains d’entre eux.

4.1. Fractions générales

Le package amsmath définit la commande \genfrac, qui produit une fraction généralisée.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Les deux premiers arguments définissent respectivement les délimiteurs gauche et droit. En utilisant le troisième argument, thick, vous pouvez remplacer l’épaisseur par défaut de la règle de fraction. Par exemple, les coefficients binomiaux (voir ci-dessous) utilisent la valeur « 0pt » pour cet argument afin de rendre la ligne invisible. La valeur par défaut (lorsqu’elle est laissée vide) de l’épaisseur du trait est déterminée par la configuration actuelle de la police pour la composition mathématique. La liste suivante contient les valeurs par défaut utilisées dans les exemples de cet article.

Style	Épaisseur par défaut
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

Le quatrième argument, style, remplace (s’il n’est pas vide) le style mathématique pour la mise en page et la taille de police utilisée. La valeur doit être comprise entre 0 et 3 : 0 - \displaystyle, 1 - \textstyle, 2 - \scriptstyle, 3 - \scriptscriptstyle. Si cet argument est laissé vide, le style est sélectionné selon les règles normales pour les fractions. Les deux derniers arguments sont le numérateur et le dénominateur.

Les anciennes commandes de fraction \over, \overwithdelims, \atop, \atopwithdelims, \above et \abovewithdelims, que le LaTeX standard hérite de TeX, produisent des avertissements lorsqu’elles sont utilisées avec le package amsmath.

4.1.1. Fractions simples

Disposant de la commande \genfrac, le package amsmath définit également trois commandes comme raccourcis pratiques : \frac, \dfrac et \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

L’exemple ci-dessous montre l’utilisation de ces commandes :

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.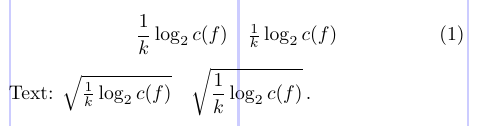

4.1.2. Coefficients binomiaux

Une autre structure semblable à une fraction est celle des coefficients binomiaux. Pour vous aider à les composer, le package amsmath fournit des commandes similaires \binom, \dbinom et \tbinom.

Voici comment ils abrégent la commande \genfrac :

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

Et voici l’exemple :

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.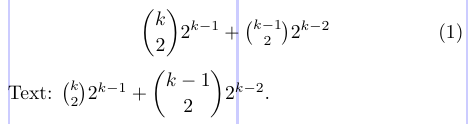

4.1.3. Fractions continues

Si vous avez besoin de composer un tableau de fractions, qui est essentiellement une fraction infinie, également connue sous le nom de « fraction continue », il existe la commande \cfrac dans le package amsmath. Passez l’argument facultatif [l] ou [r] pour aligner un numérateur à gauche ou à droite, qui est centré par défaut.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}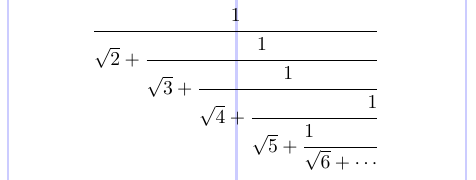

4.2. Mathématiques en boîte

Le package amsmath fournit la commande \boxed similaire à \fbox pour mettre le contenu du mode mathématique dans une boîte.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}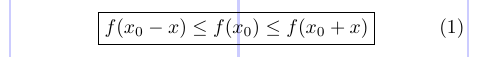

4.3. Positionner les limites

Les indices et exposants sur les intégrales, les sommes, les produits ou d’autres opérateurs peuvent être placés soit au-dessus et au-dessous de l’opérateur mathématique (la « position limite »), soit dans la position indice/exposant à droite de l’opérateur. En règle générale, les limites ne sont pas utilisées dans le texte (sinon les lignes pourraient s’étendre). Dans une formule affichée, le placement dépend de l’opérateur. L’exemple suivant montre le placement par défaut dans LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.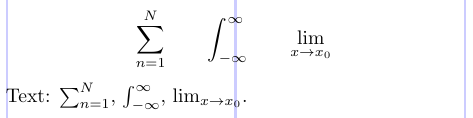

Le package amsmath offre des options pour contrôler le positionnement. Ils sont répertoriés ci-dessous, où default marque le comportement dans le cas où le package amsmath est utilisé avec une classe de document LaTeX standard mais sans aucune de ces options.

intlimits, nointlimits	Placer les exposants/indices des symboles d’intégration au-dessus et en dessous ou sur le côté (par défaut), respectivement. Utilisé uniquement dans les formules affichées.
sumlimits, nosumlimits	Placer les exposants/indices des grands opérateurs (somme, produit, etc.) au-dessus et en dessous (par défaut) ou sur le côté, respectivement. Utilisé uniquement dans les formules affichées.
namelimits, nonamelimits	Similaire à sumlimits ou nosumlimits mais pour certains opérateurs, ou « noms d’opérateurs », tels que inf, sup, lim, min, max, qui sont traditionnellement composés avec des indices en dessous, au moins lorsqu’ils apparaissent dans une formule affichée.

TeX a trois commandes primitives qui, apparues immédiatement après le symbole ou le nom de l’opérateur, contrôlent le positionnement des indices/exposants : \limits, \nolimits et \displaylimits. La commande \displaylimits produit des indices/exposants en position limite lorsque le style mathématique actuel est un style d’affichage. C’est le comportement par défaut chaque fois qu’un symbole de classe Operator apparaît ou qu’une commande \mathop est utilisée. Si vous devez composer un opérateur avec des indices/exposants en position limite en dehors d’un affichage, vous devez le déclarer individuellement à l’aide de la commande \limits.

Comparez l’exemple suivant au précédent.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.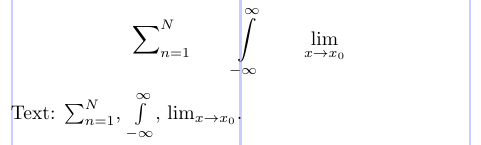

4.3. Intégrales multiples

Pour composer plusieurs signes intégraux avec des espaces bien ajustés entre eux dans le texte et les affichages, utilisez les commandes \iint, \iiint et \iiiint. Le \idotsint produit deux signes intégraux avec des points de suspension entre eux.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}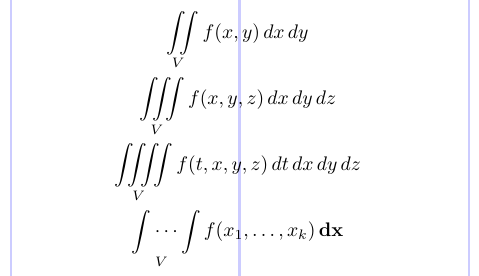

4.4. Relations modulaires

La notation « mod » pour les classes d’équivalence d’entiers est régie par les conventions d’espacement spéciales. Pour y faire face, le package amsmath propose les commandes \mod, \bmod, \pmod et \pod. L’exemple suivant montre l’utilisation de ces commandes.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}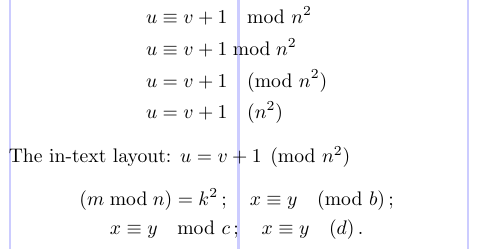

Avec amsmath, l’espacement de \pmod est diminué dans une formule non affichée.

4.5. Accents de points mathématiques

En plus des accents mathématiques \dot et \ddot, le package amsmath fournit les commandes \dddot et \ddddot, qui produisent respectivement des accents de points triples et quadruples.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Créer des exposants à partir d’accents : le package amsxtra

Le package amsxtra offre une fonctionnalité utile, une collection de commandes simples pour placer des accents en exposant dans une sous-formule :

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$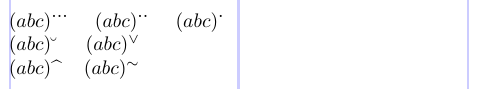

4.7. Autres décorations

LaTeX standard a la commande \stackrel qui place un exposant au-dessus d’un symbole Relation. De plus, le package amsmath définit les commandes \overset et \underset. Utilisez-le pour placer du matériel au-dessus ou en dessous de tout symbole Ordinaire ou Relation ou Opérateur binaire.

La commande \sideset ajoute des décorations à tout symbole Opérateur (somme, produit, etc.) en plus des limites normales. Ceux-ci sont placés en indice et en exposant à gauche et à droite de Opérateur.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]