7. Ajustements de prédimensionnement de la mise en page
Habituellement, LaTeX fait un excellent travail en présentant des formules mathématiques. Mais parfois, un ajustement plus fin du positionnement est nécessaire. Cet article traite de certaines techniques permettant d’affiner la mise en page afin d’améliorer un peu les formules mathématiques.
7.1. Dimensionnement et espacement automatiques
Les symboles mathématiques et les lettres deviennent généralement plus petits (et avec un espacement plus serré) lorsqu’ils apparaissent sous forme de fractions, d’indices ou d’exposants. Les formules mathématiques peuvent être présentées dans huit styles mathématiques TeX :
| D, D' | \displaystyle | Affichés sur des lignes seules |
| T, T' | \textstyle | Intégrés dans le texte |
| S, S' | \scriptstyle | En exposants ou indices |
| SS, SS' | \scriptscriptstyle | Dans tous les exposants ou indices d’ordre supérieur |
Le style de texte (T) est utilisé au niveau supérieur d’une formule définie dans le texte en cours d’exécution (entre une paire de $ ou entre \( et \)), tandis que le style d’affichage est utilisé au niveau niveau supérieur d’une formule affichée (entre une paire de $$ ou entre \[ et \]). Quant aux sous-formules, le style peut être déterminé à partir du tableau suivant :
| D | S | S' | T | T' |
| D' | S' | S' | T' | T' |
| T | S | S' | S | S' |
| T' | S' | S' | S' | S' |
| S, SS | SS | SS' | SS | SS' |
| S’, SS' | SS' | SS' | SS' | SS' |
L’exemple suivant illustre les différents styles :
1\normalsize %% Style:
2\[ b %% D
3 ^0 %% S
4 + %% D
5 \frac{(k + p) %% T
6 _{j'} %% S'
7 % \displaystyle
8 \pm %% T [D]
9 \frac{(f + q) %% S [T]
10 ^{(pk) %% SS [S]
11 ^y %% SS
12 _{j'}}} %% SS'
13 {(h + y)}} %% S' [T']
14 {(l + q) %% T'
15 ^{(pk)}} %% S'
16\]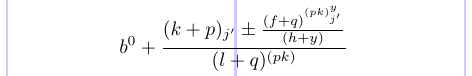
Vous pouvez supprimer le caractère de commentaire (%) avant \displaystyle et voir comment certains styles ont changé pour ceux entre parenthèses :
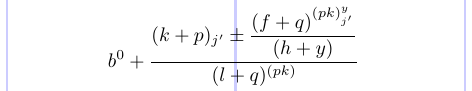
Il montre comment spécifier explicitement le style à utiliser dans chaque partie.
7.2. Sous-formules
Dans le texte, une paire d’accolades indique un groupe, ou une portée, dans lequel une déclaration est en vigueur. Dans une formule mathématique, ils délimitent en outre une sous-formule, qui est toujours composée comme une entité distincte ajoutée à la formule externe. En conséquence, les sous-formules sont toujours composées à leur largeur naturelle et ne s’étirent ni ne rétrécissent horizontalement lorsque TeX construit un paragraphe en essayant d’ajuster la formule sur une ligne. Nous avons déjà montré que la sous-formule d’un simple groupe d’accolades est traitée comme s’il s’agissait d’un seul symbole. Cela signifie qu’un groupe vide produit un symbole invisible qui peut modifier l’espacement.
Le contenu des indices/exposants et les arguments de nombreuses commandes (mais pas toutes), telles que \frac et \mathrel, sont également des sous-formules. Ainsi, ils bénéficient du même traitement spécial. L’argument de \bm, par exemple, n’est pas nécessairement défini comme une sous-formule, et c’est l’une des exceptions importantes. Dans une formule mathématique, si vous avez uniquement besoin de limiter la portée d’une déclaration, définissez un groupe en utilisant \begingroup et \endgroup. N’oubliez pas que les déclarations mathématiques spécialisées, telles que les changements de style, s’appliquent jusqu’à la fin de la sous-formule actuelle, que d’autres groupes soient présents ou non.
7.3. Grands délimiteurs
LaTeX définit quatre commandes - \big, \Big, \bigg et Bigg - pour fournir un contrôle direct de la taille des délimiteurs extensibles. Ils prennent un seul argument, qui doit être un délimiteur extensible, et produisent des versions plus grandes du délimiteur, de 1,2 à 3 fois la taille de base.
Il existe également trois variantes pour chacune des quatre commandes, donnant quatre tailles de Symbole d’ouverture (\bigl, \Bigl, \biggl et \Biggl) ; quatre tailles de Symbole de relation (\bigm, \Bigm, \biggm et \Biggm) ; et quatre tailles de Symbole de fermeture (\bigr, \Bigr, \biggr et \Biggr). Ces 16 commandes doivent être utilisées avec n’importe quel symbole pouvant venir après \left, \right ou (avec eTeX) \middle (voir ce
tableau).
Les tailles de ces délimiteurs sont fixées dans le LaTeX standard. Cependant, avec le package amsmath, les tailles s’adaptent à la taille du matériau environnant, en fonction de la taille de la police et du style mathématique utilisé. Ceci est illustré dans l’exemple ci-dessous.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4 L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7 L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]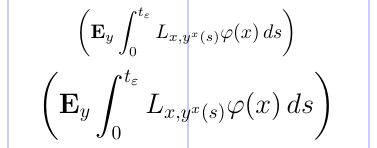
7.4. Ajustement de l’index sur un radical
Le placement de l’index sur un signe radical n’est pas toujours bon en LaTeX standard. Cependant, vous pouvez utiliser les commandes \leftroot et \uproot définies dans le package amsmath pour ajuster le positionnement de cet index. Les arguments entiers positifs de ces commandes déplacent l’index respectivement vers la gauche et vers le haut, tandis que les arguments négatifs le déplacent vers la droite et le bas. Ces arguments sont donnés en unités mathématiques, qui sont assez petites, ces commandes conviennent donc à un réglage fin.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4 \sqrt[\beta]{k} \qquad
5 \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6 \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]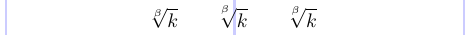
7.5. Réglage fin avec des jambes de force et des fantômes
Chaque fois que vous souhaitez composer « parfaitement » l’espacement et l’alignement mathématiques, il est généralement préférable de se tourner vers les capacités uniques et avancées de TeX primitif. L’accès à ces fonctionnalités est fourni par un certain nombre de commandes liées à \phantom et \smash. Ces commandes peuvent être utilisées soit dans des formules mathématiques, soit dans du texte en cours d’exécution.
Jetons un coup d’œil à l’exemple suivant :
1\usepackage{amsmath}
2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
5\newcommand\bfE{\mathbf{E}}
6% -------------------------------------------------------------------------------
7\begin{equation} \begin{split}
8 f_{h, \ve}(x, y)
9 &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du \\
10 &= h \int L_{x, z} \vf(x) \rho_x(dz) \\
11 &\relphantom{=} {} + h \biggl[
12 \frac{1}{\tve}
13 \biggl( \bfE_{y} \int_0^{\tve} L_{x, y^x(s)} \vf(x) \,ds
14 - \tve \int L_{x, z} \vf(x) \rho_x(dz) \biggr) + \\
15 &\relphantom{=} \phantom{{} + h \biggl[ }
16 \frac{1}{\tve}
17 \biggl( \bfE_{y} \int_0^{\tve} L_{x, y^x(s)} \vf(x) \,ds
18 - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19 \vf(x) \,ds \biggr) \biggr]
20\end{split} \end{equation}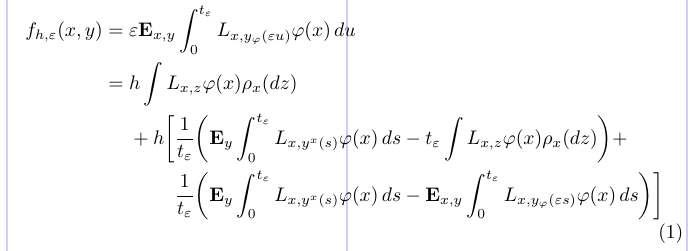
Ici, la commande \phantom obtient le positionnement horizontal ajusté. Dans le préambule, il permet de définir un symbole de relation invisible de largeur égale à son argument (= dans cet exemple). Dans les environnements mathématiques, il est utilisé pour aligner certaines lignes en les commençant par une sous-formule « fantôme » ou invisible. La paire d’accolades vide {} est la même que \mathord{}, qui produit un symbole invisible de largeur nulle nécessaire pour obtenir l’espacement correct de “+ h” (sans {}, le plus le signe produira un plus unaire avec un espacement inapproprié avant h).
Contrairement à \phantom, la commande \smash compose son contenu (dans une boîte LR) mais ignore ensuite leur hauteur et leur largeur, comme si elles étaient toutes deux nulles. La commande \hphantom, définie dans le standard LaTeX, est une combinaison des deux. Il produit l’équivalent de \smash{\phantom{some phantom content}}, c’est-à-dire une boîte invisible avec une hauteur et une profondeur nulles mais la largeur du contenu fantôme.
La commande \vphantom est similaire, mais elle rend la largeur du fantôme nulle en préservant sa hauteur totale plus sa profondeur. La commande \mathstrut est définie comme \vphantom( et produit une boîte de largeur nulle de hauteur et de profondeur égales à celles d’une parenthèse.
Avec le package amsmath, la commande \smash peut prendre un argument facultatif, de sorte que \smash[t]{...} ignore la hauteur du contenu de la boîte, en gardant la profondeur, tandis que \smash[ b]{...} ignore la profondeur, conservant la hauteur.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$
Il semble que donner au y une hauteur supplémentaire avec une entretoise rendra les radicaux similaires. Mais au lieu de cela, cela ne fait que les rendre plus différents et plus laids dans leur ensemble. Il s’avère que briser le bas du y est le meilleur moyen.
L’exemple suivant montre une utilisation très courante du smashing. La commande \smash y est utilisée pour fournir un contrôle précis sur la hauteur des délimiteurs environnants. Cela montre également que l’écrasement peut poser des problèmes car il faut connaître la hauteur réelle de la ligne. Ceci est réparé par \vphantom. \Hmjd est le symbole composé défini comme :
1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}Pour afficher l’espace vertical résultant, nous avons ajouté des règles :
| Apparence | Code | Commentaire |
|---|---|---|
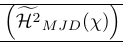 | \left( {\Hmjd } \right) | Crochets extérieurs trop grands |
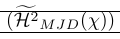 | \left( \smash{\Hmjd } \right) | Crochets extérieurs trop petits et règles trop proches |
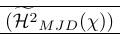 | \left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd} | Exactement comme il faut ! |
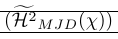 | \left( \smash[t]{\Hmjd } \right) | \vphantom et Smash partiel sont tous deux nécessaires |
Dans certains cas, des déficiences dans le traitement TeX de bas niveau peuvent conduire à des erreurs dans les détails fins de la composition. Cela peut se produire dans des mises en page particulières où (a) une sous-formule (numérateur/dénominateur d’une fraction ou indice/exposant) consiste exactement en une seule boîte LR, ou une boîte mathématique construite de manière similaire, et aussi (b) cette boîte n’a pas sa taille naturelle, comme avec les formes plus complexes de
\makebox, smashes et certains fantômes.
Pour voir cela, regardons l’exemple suivant :
1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]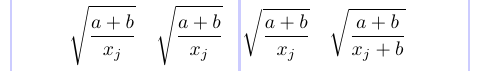
Pour réduire la profondeur du radical, un \smash a été ajouté dans le deuxième radical, mais cela n’a eu aucun effet. Dans le troisième radical, il travaillait avec un groupe d’accolades vides. Mais dans le quatrième radical, aucun groupe d’accolades vides n’était nécessaire. Pour résumer, chaque fois que vous constatez que \smash ne fonctionne pas, essayez d’ajouter une sous-formule mathématique vide ({}) avant la case isolée, pour qu’elle soit correctement traitée.
7.6. Espacement horizontal
Un réglage plus fin et plus difficile nécessite les commandes d’espacement explicites présentées dans le tableau suivant :
Les formes complètes et courtes de ces commandes sont robustes et peuvent également être utilisées en dehors des formules mathématiques dans un texte normal. Ils sont liés aux espaces fins, moyens et épais disponibles sur les machines utilisées pour composer les mathématiques au milieu du XXe siècle.
Les valeurs actuelles des trois paramètres TeX \thinmuskip, \medmuskip et \thickmuskip définissent la quantité d’espace ajoutée par ces commandes \..space. Leurs valeurs par défaut avec amsmath sont répertoriées dans le tableau. Ces paramètres de bas niveau nécessitent des valeurs en unités mathématiques (mu). Par conséquent, ils ne peuvent être définis que via des affectations TeX de bas niveau, et non par \setlength ou similaire. De plus, normalement leurs valeurs ne doivent pas être modifiées puisqu’elles sont utilisées en interne par la composition mathématique de TeX (voir le tableau suivant).
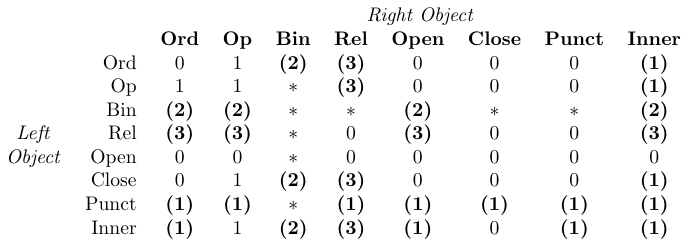
Dans le tableau, 0 signifie « pas d’espace », 1 signifie
\thinmuspace, 2 signifie\medmuskip, 3 signifie\thickmuskip, * signifie « impossible ». Les entrées en gras signifient que l’espacement correspondant n’est pas ajouté dans les styles d’écriture mathématique.
Une unité mathématique (« 1mu ») est égale à 1/18 de em dans la taille de police mathématique actuelle. Il s’ensuit que la valeur absolue d’un mu varie avec un style mathématique, donnant un espacement cohérent quel que soit le style utilisé.