8. Polices dans les formules mathématiques | LaTeX

Introduction aux police LaTeX

Contrairement au texte flottant, vous n’aurez généralement pas besoin de modifications automatiques des formes de police. Différentes formes ont des significations spécifiques en mathématiques. Par exemple, des lettres verticales en gras peuvent être utilisées pour les vecteurs. Si les caractères d’une formule devaient changer en raison des conditions environnantes, le résultat serait incorrect. C’est pourquoi la gestion des polices dans les formules mathématiques diffère de celle dans le texte.

Les caractères d’une formule peuvent être divisés en deux classes : les symboles et les caractères alphabétiques (y compris les chiffres). En fait, TeX gère en interne huit classes qui définissent un espacement approprié. Mais pour le débat actuel, la division en deux classes suffit amplement.

Certains symboles, tels que =, peuvent être saisis directement à partir du clavier. Cependant, une partie d’entre eux doit être saisie via une commande, par exemple, \leq donne un signe inférieur ou égal. L’autre groupe principal de caractères d’une formule, les caractères alphabétiques, sont saisis directement à partir du clavier.

Il existe plus de 200 symboles prédéfinis dans LaTeX standard. Il permet à l’utilisateur de composer presque toutes les formules souhaitées. Ces symboles sont situés dans un certain nombre de polices différentes, mais ils sont accessibles de telle manière que l’utilisateur n’a pas besoin de savoir comment ils sont représentés en interne. Si nécessaire, des polices de symboles supplémentaires peuvent être rendues accessibles de la même manière.

Les symboles et les caractères alphabétiques présentent une différence qui est la plus importante pour nous actuellement : les symboles ont la même représentation graphique dans une formule, tandis que l’utilisateur peut modifier l’apparence des caractères alphabétiques. Les commandes qui modifient l’apparence des caractères alphabétiques dans une formule sont appelées identifiants d’alphabet mathématique, et les polices associées à ces commandes sont appelées alphabets mathématiques. Une formule ne change pas si elle est placée, par exemple, dans un environnement de théorème où le texte est composé en italique par défaut, car les identifiants alphabétiques sont indépendants des commandes de police environnantes en dehors de la formule. Ce comportement est très important car les formes de caractères portent des significations qui doivent rester inchangées partout où la formule apparaît dans un document.

8.1. Identificateurs de l’alphabet mathématique

Un alphabet et un grand nombre de symboles ne suffisent pas aux scientifiques. Ils essaient d’utiliser toutes les polices disponibles pour désigner des concepts particuliers. En plus des alphabets étrangers tels que les lettres grecques, qui sont généralement accessibles sous forme de symboles - \alpha, \beta, etc. - nous pouvons trouver des lettres sans empattement pour les matrices, des lettres en gras avec empattement pour les vecteurs, des polices Fraktur pour les groupes, idéaux ou domaines. D’autres utilisent des formes calligraphiques pour désigner des ensembles. Le nombre de conventions est infini et elles diffèrent d’une discipline à l’autre. Et LaTeX s’adapte à cela, permettant de déclarer de nouveaux identifiants d’alphabet mathématique et de les associer à n’importe quel groupe de formes de police souhaité au lieu de s’appuyer uniquement sur un ensemble prédéfini qui ne peut pas être étendu. Ces identifiants sont des commandes spéciales à utiliser dans une formule qui compose n’importe quel caractère alphabétique de son argument dans une police spécifique. Ces identifiants peuvent utiliser différentes polices de caractères dans différentes formules, comme nous le verrons plus tard, mais au sein d’une formule, ils sélectionnent toujours la même police quelles que soient les conditions environnantes.

Identificateurs alphabétiques prédéfinis

LaTeX possède déjà quelques identifiants alphabétiques intégrés. Ils sont présentés dans le tableau ci-dessous. Les deux dernières lignes montrent que les lettres utilisées dans les formules sont tirées de l’alphabet mathématique « \mathnormal ». D’un autre côté, les lettres produites par \mathit ont un espacement différent, ce qui signifie que cet alphabet peut être utilisé pour fournir des noms de variables complets qui sont courants dans certaines disciplines.

905 / 5,000

Commande	Exemple de code	Résultat
\mathcal	$\mathcal{A}=a$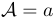
\mathrm	$\mathrm{max}_i$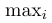
\mathbf	$\sum x = \mathbf{v}$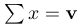
\mathsf	$\mathsf{G}_1^2$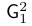
\mathtt	$\mathtt{W}(a)$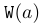
\mathnormal	$\mathnormal{abc}=abc$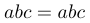
\mathit	$differ\neq\mathit{differ}$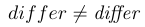

Dans LaTeX2e, les identifiants de l’alphabet mathématique sont des commandes avec un argument, une seule lettre ou un seul mot à composer dans une police spéciale.

Therefore, $\mathsf{G}$ can be computed as
\begin{equation}
\mathsf{G} = \mathcal{A} +
             \sum_{i=1}^{n} \mathcal{B}_{i}
\end{equation}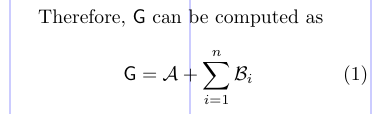

Alphabet mathématique par défaut

Si vous ne spécifiez pas explicitement un identifiant d’alphabet, à partir de quel alphabet les caractères de l’alphabet sont-ils sélectionnés ? En d’autres termes, quel est l’alphabet mathématique par défaut ? La réponse est qu’il n’existe pas d’alphabet mathématique par défaut. Le système LaTeX peut être configuré de manière à ce que les caractères alphabétiques soient récupérés à partir de différents alphabets, à moins que l’utilisateur n’en demande explicitement un spécifique, et c’est normalement le cas, comme le montre l’exemple suivant.

\begin{eqnarray}
x &=& 12345 \\
\mathrm{x} &=& \mathrm{12345} \\
\mathnormal{x} &=& \mathnormal{12345}
\end{eqnarray}

Ici, vous pouvez voir que \mathrm ne change pas les chiffres et \mathnormal ne change pas les lettres, donc la valeur par défaut pour les chiffres dans la configuration normale est l’alphabet mathématique associé à \mathrm et le La valeur par défaut pour les lettres est celle associée à \mathnormal. Ce comportement peut être contrôlé avec la commande \DeclareMathSymbol.

Quelle police LaTeX utilise-t-il pour les mathématiques ?

Dans LaTeX, la police par défaut utilisée pour le mode mathématique est généralement Computer Modern. Cependant, vous pouvez également utiliser différentes polices en les spécifiant dans le préambule de votre document LaTeX à l’aide de packages.

Identifiants alphabétiques personnalisés

Vous pouvez utiliser la commande \DeclareMathAlphabet pour définir un nouvel identifiant d’alphabet mathématique. Supposons que vous souhaitiez créer une police de caractères inclinée sans empattement disponible en tant qu’alphabet mathématique. Vous décidez d’abord d’un nouveau nom de commande, tel que \msfsl, à utiliser comme identifiant alphabétique. Ensuite, vous vous référez au tableau de classification des polices ci-dessous pour trouver un groupe de formes de police approprié à attribuer à cet identifiant alphabétique.

Vous constaterez que la famille Computer Modern Sans, par exemple, se compose d’une série moyenne aux formes verticales et inclinées. Si vous décidez d’utiliser la forme inclinée de cette famille, vous l’indiquez à LaTeX en utilisant \DeclareMathAlphabet.

\DeclareMathAlphabet{cmd}{encoding}{family}{series}{shape}

Il y a quatre paramètres (outre l’identifiant lui-même) dans la déclaration : le nom de l’encodage, la famille, la série et la forme de la police à utiliser. L’identifiant alphabétique défini dans l’exemple suivant passera toujours à Computer Modern Sans moyen incliné.

\DeclareMathAlphabet{\msfsl}{OT1}{cmss}{m}{sl}
% -------------------------------------------------------------------------------
We demonstrate this with the formula
\begin{equation}
\sum \msfsl{A}_{i} = a \tan \beta
\end{equation}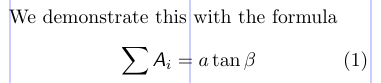

Vous pouvez également redéfinir un identifiant d’alphabet mathématique existant dans un fichier de package ou dans le préambule de votre document. Par exemple,

\DeclareMathAlphabet{\mathsf}{OT1}{pag}{m}{n}

remplacera les paramètres par défaut pour l’identifiant alphabétique \mathsf. Il passera à Adobe Avant Garde dans vos formules.

Notez que si l’alphabet mathématique en question fait partie d’une police de symboles déjà chargée par LaTeX pour d’autres raisons (par exemple, \mathcal), il est préférable d’utiliser \DeclareSymbolFontAlphabet car il utilise mieux les ressources quelque peu limitées de TeX pour les mathématiques.

Meilleures polices mathématiques

Outre la police par défaut Computer Modern, LaTeX propose sept polices intégrées pour la composition des alphabets mathématiques, afin que les utilisateurs puissent personnaliser leurs expressions mathématiques sans avoir besoin de packages supplémentaires dans le préambule. Et la meilleure option pour vous est d’utiliser l’une de ces 8 polices.

Police	Utilisation	Commande
Roman droit	Police droite standard	\mathrm{}
Calligraphique	Utilisé pour la composition de lettres mathématiques normales.	\mathnormal{}
Calligraphique	Utilisé pour composer des lettres majuscules avec une police calligraphique spéciale.	\mathcal{}
Lettres italiques	Mettre le texte en italique	\mathit{}
Upright Sans Serif	Définit des lettres Sans Serif droites	\mathsf{}
Roman droit gras	Utilisé pour la composition de lettres romaines droites en gras	\mathbf{}
Type de machine à écrire	Utilisé pour la composition de lettres de type machine à écrire droites.	\mathtt{}

8.2. Commandes de police de texte en mathématiques

Bien que les déclarations de police de texte comme \rmfamily ne puissent pas être utilisées en mathématiques, les commandes de changement de police - par exemple \textrm - peuvent être utilisées à la fois en texte et en mathématiques. À l’aide de ces commandes, vous pouvez passer temporairement du contexte mathématique au contexte textuel et composer du texte au milieu de votre formule qui fait logiquement partie du texte environnant en dehors de la formule. La police utilisée pour composer ce texte dépendra des conditions environnantes, ce qui signifie qu’elle héritera de l’encodage, de la famille, de la série et de la forme actuels, comme dans l’exemple ci-dessous.

\sffamily The result will be
\[ x = 10 \textbf{ and thus } y = 12 \]

Ici, nous pouvons voir que la famille Sans a été conservée et que la série a été modifiée en gras. La commande \text fournie par le package amstext (qui est également chargé par amsmath) peut s’avérer plus utile. Il récupère les valeurs actuelles d’encodage, de famille, de série et de forme sans aucune modification.

8.3. Versions de formules mathématiques

Nous avons expliqué comment modifier des parties d’une formule à l’aide d’identifiants de l’alphabet mathématique. LaTeX vous permet également de modifier l’apparence d’une formule dans son ensemble. Les formules mathématiques sont toujours composées dans une certaine version mathématique. Et vous pouvez basculer entre les versions mathématiques en dehors du mode mathématique en utilisant la commande « \mathversion », qui modifie la disposition globale des formules suivantes.

LaTeX a deux versions mathématiques par défaut : normal et gras. Et des packages spéciaux fournissent plus de versions. Par exemple, le package mathtime (pour les polices commerciales MathTime) configure une version mathématique appelée heavy pour composer des formules avec des symboles ultra gras comme ceux fournis par les polices MathTime.

Évidemment, la version mathématique par défaut est \mathversion{normal}. La version grasse, à son tour, produira des caractères alphabétiques et des symboles plus gras, bien que les gros opérateurs, comme \sum, ne soient pas modifiés par défaut. L’exemple ci-dessous montre la même formule d’abord dans la version mathématique normale, puis dans la version mathématique en gras.

\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}
\mathversion{bold}
\begin{equation}
  \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
\end{equation}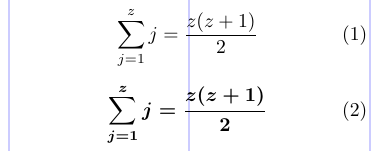

Utiliser \mathversion peut convenir dans certaines situations, comme dans les titres, mais vous devez garder à l’esprit que changer la version signifie changer l’apparence et éventuellement la signification de la formule entière. Si vous souhaitez assombrir uniquement certains symboles ou caractères dans une formule, vous devez utiliser l’identifiant alphabétique \mathbf pour les caractères et/ou utiliser la commande \bm fournie par le package bm plutôt que changez le \mathversion.

Lorsque vous modifiez la version mathématique, LaTeX recherche dans ses tableaux internes où se trouvent tous les symboles de cette nouvelle version mathématique. Il peut également modifier tout ou partie des identifiants de l’alphabet mathématique et les associer à d’autres formes de police dans cette version.

Mais qu’arrive-t-il aux identifiants alphabétiques personnalisés comme \msfsl que nous avons définis dans l’ exemple ? Tant que vous les avez déclarés en utilisant \DeclareMathAlphabet, ils resteront les mêmes dans toutes les versions mathématiques.

Si l’identifiant de l’alphabet mathématique doit produire une police différente dans une version mathématique spéciale, vous devez en informer LaTeX en utilisant la commande \SetMathAlphabet. Par exemple, dans la configuration par défaut, l’identifiant alphabétique \mathsf est défini comme suit :

\DeclareMathAlphabet{\mathsf}{OT1}{cmss}{m}{n}
\SetMathAlphabet{\mathsf}{bold}{OT1}{cmss}{bx}{n}

La première ligne définit le support Computer Modern Sans comme valeur par défaut pour \mathsf dans toutes les versions mathématiques. La deuxième ligne demande à LaTeX d’utiliser Computer Modern Sans bold étendu dans la version mathématique en gras.

\SetMathAlphabet{cmd}{version}{encoding}{family}{series}{shape}

Comme vous l’avez peut-être deviné dans l’exemple précédent, \SetMathAlphabet prend six arguments : l’identifiant de l’alphabet mathématique, le nom de la version mathématique pour laquelle vous définissez une configuration spéciale et quatre paramètres pour identifier la police à laquelle vous l’associez. votre configuration. Comme nous l’avons noté précédemment, vous pouvez redéfinir un identifiant d’alphabet mathématique existant en utilisant \DeclareMathAlphabet. Si vous le faites, toutes les déclarations \SetMathAlphabet précédentes pour cet identifiant sont supprimées de la mémoire interne de LaTeX. Ainsi, l’identifiant sera le même dans toutes les versions mathématiques, à moins que vous n’y ajoutiez de nouvelles déclarations \SetMathAlphabet.

8.4. Réglage des polices dans les formules avec les packages AMS-LATEX

Le package amsfonts (et amssymb) définit deux alphabets mathématiques : l’alphabet d’Euler Fraktur (\mathfrak) et l’alphabet Blackboard Bold (\mathbb). Voir l’exemple ci-dessous.

\usepackage{amsfonts}
% -------------------------------------------------------------------------------
$ \forall n \in \mathbb{N} : \mathfrak{M}_n \leq \mathfrak{A} $

5. Style de police mathématique gras. Le paquet bm

Pour les lettres latines uniquement, vous pouvez utiliser la commande \mathbf. Pour tout le reste, il existe le package bm. Chargez-le simplement et utilisez \bm pour rendre n’importe quelle formule aussi audacieuse et belle que le permettent les polices disponibles.

L’exemple suivant montre de nombreuses façons d’utiliser les commandes \bm et \mathbf. Il montre également une stratégie pour définir des noms abrégés pour les symboles gras fréquents, en utilisant à la fois les standards \newcommand et \bmdefine de LaTeX, qui sont fournis par le package bm. Notez que \mathbf{xy} n’est pas identique à \bm{xy}. Le premier produit un “xy” romain gras et le second produit “xy” (italique gras et mathématique).

\usepackage{amsmath,amssymb,bm}
\newcommand\bfB{\mathbf{B}} \newcommand\bfx{\mathbf{x}}
\bmdefine\bpi{\pi} \bmdefine\binfty{\infty}
% -------------------------------------------------------------------------------
\section{The bold equivalence
  $\sum_{j < B} \prod_\lambda : \bm{\sum_{x_j} \prod_\lambda}$}
\begin{gather}
  B_\infty + \pi B_1 \sim \bfB_{\binfty} \bm{+} \bpi \bfB_{\bm{1}}
    \bm {\sim B_\infty + \pi B_1}\\
  B_\binfty + \bpi B_{\bm{1}} \bm{\in} \bm{\biggl\lbrace}
    (\bfB, \bfx) : \frac {\partial \bfB}{\partial\bfx}
    \bm{\lnapprox} \bm{1} \bm{\biggr\rbrace}
\end{gather}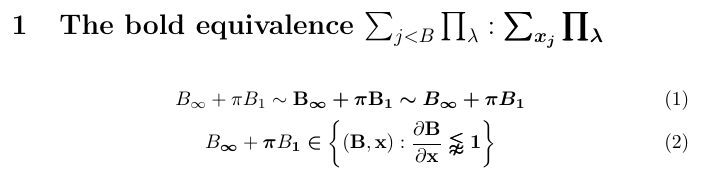

Dans cet exemple, « bm » fait de son mieux pour répondre aux demandes de versions en gras de symboles et de lettres individuels. Mais si vous y regardez bien, vous verrez que les résultats ne sont pas toujours optimaux. Par exemple, les opérateurs somme et produit sont réalisés avec une technique connue sous le nom de poor man’s bold, dans laquelle le symbole est surimprimé trois fois avec de légers décalages. De plus, les accolades ne sont pas du tout mises en gras. De tels inconvénients ne peuvent être évités car pour certains symboles, il n’existe tout simplement pas de variante en gras lors de l’utilisation des polices mathématiques Computer Modern.

Quelles sont les règles exactes que \bm suit pour produire des formes en gras des symboles dans son argument ? En général, il utilise le fait que LaTeX inclut une version mathématique gras (accessible via \boldmath) pour composer une formule entière en gras (à condition que des polices grasses appropriées soient disponibles et configurées). Pour chaque symbole, la commande \bm examine cette version mathématique pour voir ce qui serait fait dans cette version. Si la police sélectionnée pour le symbole est différente de celle sélectionnée dans la version mathématique normale, il compose alors le symbole dans cette police en gras, obtenant un résultat parfait (en supposant que la version mathématique en gras a été correctement configurée). Si les polices des deux versions sont identiques, il suppose qu’aucune variante en gras n’est disponible et applique le gras du pauvre.

Chargez le paquet bm après les paquets qui modifient la configuration de police mathématique existante !

La situation est encore plus complexe avec les délimiteurs, tels que \biggl\lbrace dans l’exemple. TeX compose généralement un délimiteur par un glyphe choisi pour correspondre à une hauteur demandée à partir d’une séquence de différentes tailles. Ces glyphes peuvent être situés dans différentes polices, et une taille particulière peut avoir ou non des variantes en gras. Tout cela ensemble rend impossible pour \bm de déterminer de manière fiable s’il doit appliquer l’audace du pauvre. Il compose donc le délimiteur en utilisant les polices proposées par la version mathématique en gras. Avec les polices mathématiques Computer Modern, seule la plus petite taille de délimiteur est disponible en gras ; toutes les autres tailles proviennent de polices qui n’ont pas de variantes grasses.

\usepackage{bm}
% -------------------------------------------------------------------------------
$\bm{\Biggl\lbrace\biggl\lbrace\Bigl\lbrace\bigl \lbrace \lbrace
  \mathcal{Q}
  \rangle \bigr\rangle\Bigr\rangle\biggr\rangle
\Biggr\rangle}$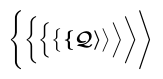

Normalement, si une commande qui elle-même prend des arguments se trouve dans l’argument de \bm, alors cette commande doit être entièrement incluse dans l’argument de \bm. En conséquence, toutes les parties du matériel mis en page seront en gras. Si vous avez besoin que le résultat d’une commande avec des arguments ne soit que partiellement en gras, vous devez procéder comme suit. Vous devez mettre le(s) symbole(s) que vous ne voulez pas mettre en gras dans une \mbox et réinitialiser explicitement la version mathématique dans le contenu de la boîte en utilisant \unboldmath. TeX considère une \mbox comme un symbole de classe Ordinary. Ainsi, pour obtenir le bon espacement, vous devrez peut-être l’entourer d’un \mathbin, \mathrel ou \mathop.

\usepackage{amsmath,bm}
% -------------------------------------------------------------------------------
$ \bm{\sqrt[2]{x \times \alpha}} $ but
$ \bm{\sqrt[2]{x \mathbin{\mbox{\unboldmath$\times$}} \alpha}} $
or the similar
$ \bm{\sqrtsign}{\bm{x} \times \bm{\alpha}} $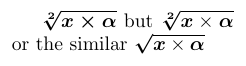

Heureusement, des opérations aussi complexes sont rarement nécessaires. Dans la plupart des cas impliquant des commandes avec des arguments, seules certaines parties de l’argument doivent être mises en gras. Et cela peut être réalisé en utilisant la commande \bm dans ces arguments. Comme avec \sqrtsign dans l’exemple précédent, pour le cas courant des accents gras, \bm est spécialement programmé pour permettre à l’argument de l’accent d’être en dehors de son propre argument. Toutefois, si vous avez régulièrement besoin de tels accents, il est préférable de définir vos propres abréviations, comme dans l’exemple ci-dessous.

Amélioration des performances

Bien que \bmdefine\bpi{\pi} semble être simplement un raccourci pour \newcommand\bpi{\bm{\pi}}, en fait la vérité est presque le contraire : \bm définit un nouveau temporaire caché commande utilisant \bmdefine puis utilise immédiatement cette commande temporaire pour produire le symbole en gras. En d’autres termes, \bmdefine fait tout le travail ! Si vous utilisez fréquemment, par exemple, quelque chose qui est défini via \bm{\alpha}, alors un nouveau \bmdefine est exécuté à chaque fois. Si vous fournissez la définition \bmdefine\balpha{\alpha} dans le préambule, alors \bmdefine ne fait son travail fastidieux qu’une seule fois, quel que soit le nombre de fois \balpha est utilisé.

\usepackage{bm}
\bmdefine\bhat{\hat}
% -------------------------------------------------------------------------------
$\hat a \neq \bm{\hat a} \neq \bm\hat a = \bhat a\neq \bm\widehat a$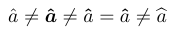

Cet exemple montre également que les accents à largeur variable (par exemple, \widehat) partagent un défaut avec les délimiteurs : dans la configuration mathématique Computer Modern, ils proviennent d’une police pour laquelle aucune variante en gras n’est disponible.