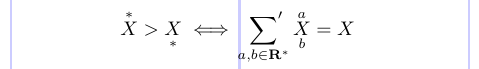4. Декоративные символы и составные конструкции | LaTeX

Пакет amsmath предоставляет некоторые команды для создания структур, таких как дробные объекты и декорированные символы. В этом обсуждении рассматриваются некоторые из них.

4.1. Общие дроби

Пакет amsmath определяет команду \genfrac, которая производит обобщенную дробь.

\genfrac{ldelim}{rdelim}{thick}{style}{num}{denom}

Первые два аргумента определяют левый и правый разделители соответственно. Используя третий аргумент thick, вы можете переопределить толщину по умолчанию правила дроби. Например, биноминальные коэффициенты (см. ниже) используют для этого аргумента значение «0pt», чтобы сделать линию невидимой. Значение по умолчанию (если оно оставлено пустым) толщины линии определяется текущей настройкой шрифта для математического набора текста. В следующем списке приведены значения по умолчанию, используемые в примерах этой статьи.

Стиль	Толщина по умолчанию
text/display	0.4pt
script	0.34pt
scriptscript	0.24pt

Четвертый аргумент, style, переопределяет (если не оставлен пустым) математический стиль используемого макета и размера шрифта. Значение должно находиться в диапазоне 0–3: 0 – \displaystyle, 1 – \textstyle, 2 – \scriptstyle, 3 – \scriptstyle. Если этот аргумент оставить пустым, стиль выбирается в соответствии с обычными правилами для дробей. Последние два аргумента — это числитель и знаменатель.

The old fraction commands \over, \overwithdelims, \atop, \atopwithdelims, \above, and \abovewithdelims, which standard LaTeX inherits from TeX, produce warnings when they are used with the amsmath package.

4.1.1. Простые дроби

Имея команду \genfrac, пакет amsmath также определяет три команды как удобные сокращения: \frac, \dfrac и \tfrac.

\newcommand\frac [2]{\genfrac{}{}{}{}{#1}{#2}}
\newcommand\dfrac[2]{\genfrac{}{}{}{0}{#1}{#2}}
\newcommand\tfrac[2]{\genfrac{}{}{}{1}{#1}{#2}}

Пример ниже демонстрирует использование этих команд:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \frac{1}{k} \log_2 c(f)
  \quad \tfrac{1}{k} \log_2 c(f)
\end{equation}
Text: $ \sqrt{ \frac{1}{k} \log_2 c(f) } \quad
        \sqrt{ \dfrac{1}{k} \log_2 c(f) }\, $.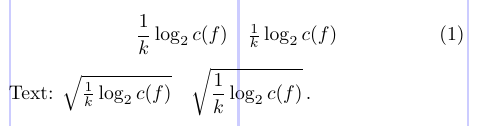

4.1.2. Биномиальные коэффициенты

Другая дробная структура — это биномиальные коэффициенты. Чтобы помочь вам их верстать, пакет amsmath предоставляет аналогичные команды \binom, \dbinom и \tbinom.

Вот как они сокращают команду \genfrac:

\newcommand\binom[2]{\genfrac{(}{)}{0pt}{}{#1}{#2}}
\newcommand\dbinom[2]{\genfrac{(}{)}{0pt}{0}{#1}{#2}}
\newcommand\tbinom[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}

И вот пример:

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \binom{k}{2} 2^{k - 1} + \tbinom{k - 1}{2} 2^{k - 2}
\end{equation}
Text: $ \binom{k}{2} 2^{k - 1} + \dbinom{k - 1}{2} 2^{k - 2} $.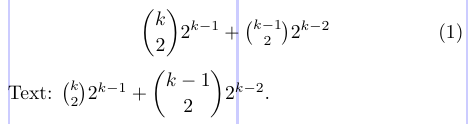

4.1.3. Непрерывные дроби

Если вам нужно набрать массив дробей, который по сути представляет собой бесконечную дробь, также известную как «непрерывная дробь», в пакете amsmath есть команда \cfrac. Передайте необязательный аргумент [l] или [r], чтобы выровнять числитель влево или вправо, который по умолчанию центрируется.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation*}
\cfrac {1}{\sqrt{2} +
  \cfrac {1}{\sqrt{3} +
    \cfrac {1}{\sqrt{4} +
      \cfrac[r] {1}{\sqrt{5} +
        \cfrac[l] {1}{\sqrt{6} + \dotsb }
}}}}
\end{equation*}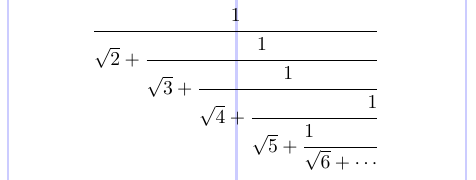

4.2. Коробочная математика

Пакет amsmath предоставляет команду \boxed, аналогичную \fbox, для помещения содержимого математического режима в поле.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{equation}
  \boxed { f(x_0 - x) \leq f(x_0) \leq f(x_0 + x) }
\end{equation}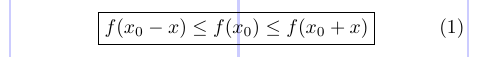

4.3. Расстановка пределов

Нижние и верхние индексы интегралов, сумм, произведений и других операторов могут располагаться либо над и под математическим оператором («предельная позиция»), либо в позиции нижнего/верхнего индекса справа от оператора. Обычно лимиты в тексте не используются (иначе строки могут расползаться). В отображаемой формуле размещение зависит от оператора. В следующем примере показано размещение по умолчанию в LaTeX.

\[
\sum_{n=1}^N \qquad \int_{-\infty}^\infty \qquad \lim_{x \to x_0}
\]
Text: $\sum_{n=1}^N$, $\int_{-\infty}^\infty$, $\lim_{x \to x_0}$.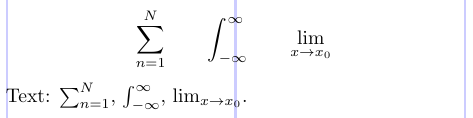

Пакет amsmath предлагает опции для управления позиционированием. Они перечислены ниже, где default обозначает поведение в случае, если пакет amsmath используется со стандартным классом документа LaTeX, но без какой-либо из этих опций.

intlimits, nointlimits	Размещать верхние/нижние индексы символов интегрирования выше и ниже или сбоку (по умолчанию) соответственно. Используется только в отображаемых формулах.
sumlimits, nosumlimits	Размещать верхние/нижние индексы больших операторов (сумма, произведение и т. д.) выше и ниже (по умолчанию) или сбоку соответственно. Используется только в отображаемых формулах.
namelimits, nonamelimits	Аналогично sumlimits или nosumlimits, но для определенных операторов или «имен операторов», таких как inf, sup, lim, min, max, которые традиционно набираются с нижними индексами внизу, по крайней мере, когда они встречаются в отображаемой формуле.

В TeX есть три примитивные команды, которые появляются сразу после имени символа или оператора и управляют расположением индексов/надстрочных индексов: \limits, \nolimits и \displaylimits. Команда \displaylimits создает нижние/верхние индексы в предельном положении, когда текущий математический стиль является стилем отображения. Это поведение по умолчанию всякий раз, когда появляется символ класса Operator или используется команда \mathop. Если вам необходимо набрать оператор с нижними/верхними индексами в предельной позиции вне отображения, вы должны объявить его индивидуально с помощью команды \limits.

Сравните следующий пример с предыдущим.

\[
\sum\nolimits_{n=1}^N \qquad \int\limits_{-\infty}^\infty \qquad \lim\displaylimits_{x \to x_0}
\]
Text: $\sum\nolimits_{n=1}^N$, $\int\limits_{-\infty}^\infty$, $\lim\displaylimits_{x \to x_0}$.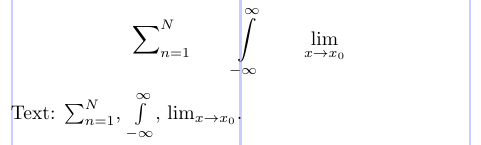

4.3. Множественные интегралы

Чтобы набрать несколько целочисленных знаков с хорошо отрегулированными пробелами между ними как в тексте, так и на дисплеях, используйте команды \iint, \iiint и \iiiint. \idotsint создает два целых знака с многоточием между ними.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{gather*}
\iint \limits _V f(x,y) \,dx \,dy \\
\iiint \limits _V f(x,y,z) \,dx \,dy \,dz \\
\iiiint \limits _V f(t,x,y,z) \,dt \,dx \,dy \,dz \\
\idotsint \limits _V f(x_1, \dots, x_k) \,\mathbf{dx}
\end{gather*}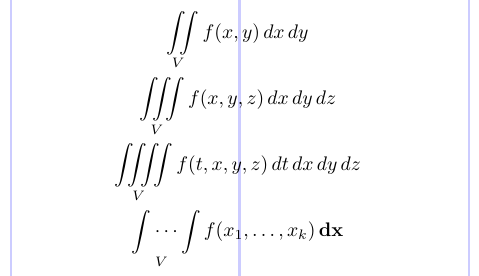

4.4. Модульные отношения

Обозначение «mod» для классов эквивалентности целых чисел регулируется специальными соглашениями о пробелах. Чтобы справиться с этим, пакет amsmath предлагает команды \mod, \bmod, \pmod и \pod. В следующем примере показано использование этих команд.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
\begin{align*}
u & \equiv v + 1 \mod{n^2} \\
u & \equiv v + 1 \bmod{n^2} \\
u & = v + 1 \pmod{n^2} \\
u & = v + 1 \pod{n^2}
\end{align*}
The in-text layout: $ u = v + 1 \pmod{n^2} $
\begin{gather*}
(m \bmod n) = k^2 \, ; \quad x \equiv y \pmod b \, ; \\
x \equiv y \mod c \, ; \quad x \equiv y \pod d\, .
\end{gather*}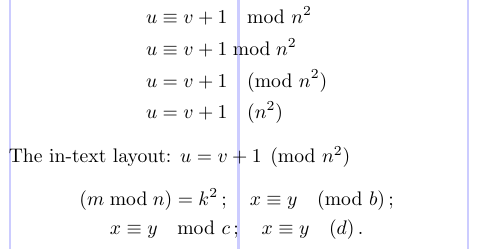

With amsmath, the spacing of \pmod is decreased within a non-displayed formula.

4.5. Математические точечные акценты

В дополнение к математическим акцентам \dot и \ddot, пакет amsmath предоставляет команды \dddot и \ddddot, которые создают тройные и четверные точечные акценты соответственно.

\usepackage{amsmath}
% -------------------------------------------------------------------------------
$ \dot{A} \quad \ddot{B} \quad \dddot{C} \quad \ddddot{D} $

4.6. Создание надстрочных индексов из диакритических знаков: пакет amsxtra

Пакет amsxtra предлагает полезную функцию — набор простых команд для расстановки диакритических знаков в качестве надстрочных индексов в подформуле:

\usepackage{amsxtra}
% -------------------------------------------------------------------------------
$(abc)\spdddot$ \quad $(abc)\spddot$ \quad $(abc) \spdot$ \\
$(abc)\spbreve$ \quad $(abc)\spcheck$ \\
$(abc)\sphat$ \quad $(abc)\sptilde$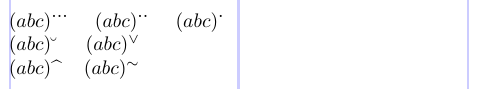

4.7. Другие украшения

В стандартном LaTeX есть команда \stackrel, которая помещает верхний индекс над символом Relation. Кроме того, пакет amsmath определяет команды \overset и \underset. Используйте его для размещения материала выше или ниже любого символа Обычный, Отношения или символа Бинарного оператора.

Команда \sideset добавляет украшения к любому символу Оператора (сумма, произведение и т. д.) в дополнение к обычным ограничениям. Они размещаются в нижних и верхних позициях слева и справа от Оператора.

\[ \overset{*}{X} > \underset{*}{X}
\iff \sideset{}{'}\sum_{a,b \in \mathbf{R^*}}
\overset{a}{\underset{b}{X}} = X \]